Навигация
Педагогическая концепция развития математического мышления на основе дифференцированного обучения
2. Педагогическая концепция развития математического мышления на основе дифференцированного обучения
2.1 Психолого-педагогическая диагностика интересов учащихсяПрежде чем приступить к рассмотрению методики дифференцированного обучения математике в лицее рассмотрим методику изучения способностей.
Диагностические особенности метода - в основу работы закладывается изучение способностей личности.
В структуре математических способностей в педагогической литературе выделяются более 10 групп компонентов [51]. Мы предполагаем проанализировать два основных компонента математических способностей: быстроту усвоения и активность мышления.
1 группа – быстрота усвоения, характеризуется следующими категориями:
1) дословное повторение текста;
2) частичное повторение;
3) воспроизведение 50% текста;
4) самостоятельное воспроизведение ранее изученного текста;
5) воспроизведение материала с помощью учителя;
6) воспроизведение с ошибками, но основная нить вопроса удерживается;
7) замедленное, невнятное воспроизведение текста;
8) умственная отсталость (затухание развития).
2 группа - активность мышления, характеризуется пятью категориями:
1) плодотворная работа на протяжении всего занятия;
2) работа со «вспышками»;
3) неполная работоспособность;
4) быстрая утомляемость;
5) игнорирование заданий.
Указанные категории позволяют выделить три уровня математических способностей:
Уровень А – учащиеся, имеющие хорошие математические способности (1 группа, категории 1)-4); 2 группа, категории 1)-2)). Уровень В – учащиеся, имеющие средние математические способности (1 – 4)-6); 2 – 2)-3)).Уровень С – учащиеся, имеющие низкие математические способности (1 –7)-8); 2 – 4)-5)).
Составляем таблицу и заполняем ее для каждого учащегося.
Дополнительной формой дифференцирования учащихся являются задания в тестовой форме (оперативный контроль), нацеленные на диагностику умственного развития учащихся. Рассмотрим один из них.
Это «тест достижений», где основой является не форма, а содержание заданий и который позволяет выявить знания в предметной области (в области математики).
На выполнение каждого теста отводится 30 минут. Ответы к заданиям записываются в специальные бланки.
Задания подбираются по уровням сложности.
1.Задания первого уровня усвоения – на опознание, различие или классификацию изученных объектов.
2.Второго уровня усвоения, выявляющее умение учащихся воспроизводить информацию без подсказки, по памяти для решения типовых задач. Различают следующие задания второго уровня усвоения – подстановка, конструктивные, собственно типовые.
3.Третий уровень усвоения – тесты требующие какое-то предварительное преобразование усвоенных методик и их приспособление к ситуации в задаче, т.е. требуют выполнения эвристической деятельности (применение формул сокращенного умножения в нестандартной ситуации, выявление закономерности и др.).
Тесты четвертого уровня усвоения должны выявлять творческие умения учащихся. В этих тестах нет готового эталона и о качестве его решения учащимся может судить только компетентный эксперт. Поэтому тесты этого уровня в диагностическом тестировании не применяются.
Сравнение ответа учащегося с эталоном, в котором определено число ![]() существенных операций, ведущих к решению теста, к числу правильно выполненных учащимся операций
существенных операций, ведущих к решению теста, к числу правильно выполненных учащимся операций ![]() теста дает возможность определить эффективность усвоения
теста дает возможность определить эффективность усвоения ![]() . Таким образом,
. Таким образом, ![]() .
.
Коэффициент ![]() усвоения поддается нормированию
усвоения поддается нормированию ![]() и на этой основе легко дифференцировать учащихся.
и на этой основе легко дифференцировать учащихся.
По коэффициенту усвоения ![]() судят о завершенности процесса обучения. Исследования показывают, что при
судят о завершенности процесса обучения. Исследования показывают, что при ![]() процесс обучения можно считать завершенным, т.к. в последующей деятельности учащийся способен в ходе самообучения совершенствовать свои знания.
процесс обучения можно считать завершенным, т.к. в последующей деятельности учащийся способен в ходе самообучения совершенствовать свои знания.
Далее, для каждого уровня усвоения определяем коэффициент усвоения.
Например,
![]() ,
,
где ![]() - числу правильно выполненных учащимся операций во всех тестах первого уровня,
- числу правильно выполненных учащимся операций во всех тестах первого уровня, ![]() - число существенных операций, ведущих к решению тестов первого уровня.
- число существенных операций, ведущих к решению тестов первого уровня.
В приведенных тестах, общее число операций ![]() ,
, ![]() . Положительную оценку учащийся получил бы, если выполнил правильно не менее 8 операций (
. Положительную оценку учащийся получил бы, если выполнил правильно не менее 8 операций (![]() ).
).
С учетом вышесказанного – уровень С – учащиеся уровень усвоения которых ![]() ; уровень В -
; уровень В - ![]() ; уровень А -
; уровень А - ![]() .
.
Совмещая результаты проверок быстроты усвоения и активности мышления с результатами теста, выявляем окончательное дифференцирование учащихся.
2.2 Методика развития математического мышления учащихся на основе дифференцированного обученияА теперь рассмотрим непосредственно методику дифференцированной работы на уроке.
Класс разделен на три группы А, В, С.
Первый этап – дифференцированная домашняя работа. Трем группам определяется три разных задания. Группе С на дом предлагаются задания точно соответствующие обязательным результатам обучения. Группа В выполняет такие же задания и плюс более сложные задания из учебника. Для группы А задания из учебника дополняются заданиями из различных пособий для поступающих в вузы.
Второй этап – учет знаний учащихся на уроке. На этом этапе работу учителя облегчает таблица учета знаний, в которой предусмотрены следующие графы: уровень учащегося; повторение (П); домашнее задание (Д); положительные ответы; ошибки, недочеты; общий итог, оценка.
Перед уроком каждый учащийся, подойдя к таблице, заполняет в строке возле своей фамилии клетки в графах «П» и «Д». Остальные клетки таблицы заполняет учитель во время урока.
Подчеркнем, что на таких уроках учитель не занимается непосредственной проверкой того, как учащиеся повторили теоретический материал или выполнили домашнее задание.
Третий этап – организация базового повторения, т.е. заполнение выявленных пробелов в теоретическом материале, разъяснение недочетов и ошибок в самостоятельных и контрольных работ. Материал, который планирует повторить учитель, записывается в виде таблицы на доске. При разборе каждого задания из таблицы учитель предлагает такие, например, задания:
«Выберите из данных ответов верный», «Исправьте ошибку в данном задании» - для уровня С.
«Назовите правило, по которому выполняется действие», «Закончите задание» - для уровня В.
«Поясните причину ошибки», «Дайте определения основным понятиям, использующимся в данной задаче» - для уровня А. Также учащимся уровня А можно предложить самим придумать задания и вопросы по таблице.
Четвертый этап – проверка усвоения пройденного материала. Она может проводиться в четырех режимах.
Режим «самоконтроля» предлагается учащимся из группы А, учащиеся из групп В и С поочередно работают у доски; в течении урока к работе у доски привлекаются все учащиеся класса; к доске никого не вызывают, но учащиеся рассаживаются по группам, члены групп опрашивают друг друга по заранее составленным вопросам.
Пятый этап – изучение нового материала. Каждая тема требует особого подхода к ее объяснению. Но в организационном плане можно выделить четыре урока: 1 урок – «изучаем», 2 урок – «усваиваем», 3 урок – «закрепляем», 4 урок – «углубляем».
Первый урок «изучаем» обращен одинаково ко всем учащимся. На следующих уроках проявляется дифференциация. Задания для группы А быстро переходят от обязательных к эвристическим, требующих дополнительных знаний мыслительных операций. Группа В сосредотачивается на упражнениях, которые требуют старания, хорошего понимания темы и умений сделать 1-2 логических шага в направлении развития этих положений. Задания для группы С снова и снова возвращают учащихся к основным моментам объясненной темы.
Шестой этап – самостоятельные и контрольные работы.
Самостоятельные работы делим на три вида:
1) решение по образцу (группа С);
2) выделение нужного ответа из нескольких (группа В);
3) работа с дополнительным материалом (группа А).
Контрольные работы разделяются по содержанию на базовые (когда проверяется обязательный материал) и так называемые объемные, в которые входят задания по всему материалу изученного курса. На одной и той же контрольной работе учащимся из группы А предлагаются задания, хоть и соответствующие программе, но повышенной сложности.
Для успешного овладения программным материалом, развития математического мышления мы рекомендуем:
1) определить минимум знаний, высот которых должны достичь слабые лицеисты при изучении данной темы; наметить дополнительные задания для средних и сильных лицеистов;
2) наметить систему обучающих, тренировочных и творческих заданий для различных категорий учащихся;
3) изучить уровень подготовленности учащихся к восприятию каждой новой темы (путем опроса, бесед, проведения проверочных и контрольных работ) для объединения их во временные учебные группы;
4) определить наиболее эффективные приемы сочетания коллективной, групповой и индивидуальной работы на уроке, а именно:
- к самой многочисленной группе лицеистов (В) относить учащихся, равномерно усваивающих при незначительной помощи учителя программный материал, владеющих навыками самостоятельной работы;
- к группе «сильных» лицеистов (А) относить учащихся быстро схватывающих изучаемый материал, могущих выполнять задания повышенной трудности при минимальной помощи учителя или вообще без нее;
- к группе «слабых» (С) – относить учащихся, слабо овладевающих новым материалом, недостаточно владеющих навыками самостоятельной работы, нуждающихся в постоянном внимании и контроле учителя;
- учащихся объединять во временные учебные группы на период изучения большого раздела программного материала.
При внутриклассном дифференцированном обучении организация фронтальных работ рекомендуется в тех случаях, когда все лицеисты примерно одинаково подготовлены к выполнению задания, когда каждый из них способен принять активное участие в выполнение коллективной работы.
Подготавливать учащихся к активному выполнению фронтальных заданий помогает групповая работа, направленная на искоренение и предупреждение ошибок определенной части учащихся. Таким образом, групповая работа способствует совершенствованию фронтальной, обогащает ее, делает гибкой и управляемой.
Приемы сочетания фронтальной, групповой и индивидуальной форм работ зависят от учебно-воспитальных задач урока, сложности заданий, познавательных возможностей учащихся.
Фронтальная работа успешно применяется при ознакомлении с новым, одинаково трудным для всех учащихся материалом. Но так как усвоение нового материала проходит у учащихся разными темпами, то с некоторыми из них необходима дополнительная доработка нового материала по группам. Так осуществляется переход от фронтальной работы к групповой.
При первичном закреплении знаний, как правило, выделяются сочетания групповой и индивидуальной работы; систематизация усвоенных знаний обобщается фронтально.
При последующем закреплении изученного выделяются следующие сочетания форм работ: а) закрепление осуществляется фронтально, групповая и индивидуальная работы имеют цель углубления знаний; б) закрепление изученного осуществляется в группах и индивидуально, фронтальная работа посвящается подведению итогов усвоения.
На этапе совершенствования (обобщение и систематизация) знаний выделяются следующие приемы сочетания этих форм: а) первичное применение знаний в измененных условиях и выполнение различных работ творческого характера осуществляется фронтально; приобретенные умения используются в групповой и индивидуальной работе; б) групповые и индивидуальные формы посвящены обобщению и систематизации знаний; применение знаний осуществляется во фронтальной работе.
Дифференциация заданий по математике в лицее осуществляется по следующим признакам: а) по степени самостоятельности познавательных действий, необходимых для выполнения задания; б) по степени трудности их выполнения каждым учащимся.
В свою очередь все дифференцированные задания различаются по их дидактической цели. Они могут быть направлены: на подготовку лицеистов к восприятию нового материала; на самостоятельное усвоение учащимися новых знаний; на первичное закрепление, расширение и совершенствование усвоенных знаний; на выработку, закрепление и совершенствование умений и навыков; на выполнение домашних заданий.
Похожие работы
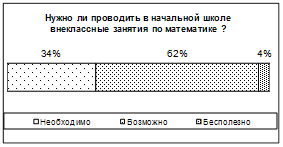
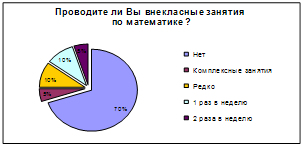
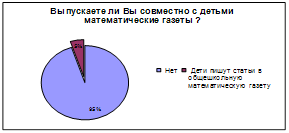
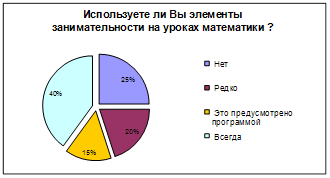
... и младших школьников. Анкета для студентов включала в себя два вопроса, один из которых о том, в чем, по их мнению, заключается развитие математических способностей школьников, а второй ¾ для выяснения отношения студентов к проведению внеклассной работы по математике в начальных классах. Анкета для преподавателей имела своей целью выяснить, проводят ли (а если проводят, то как часто) учителя ...
... и перенести полученные знания на практику. Глава 2. Работа учителя по развитию логического мышления на уроках математики 2.1 Опытно-экспериментальная работа и анализ ее результатов Опытно-экспериментальное исследование по выявлению уровня развития логического мышления школьников при решении текстовых задач проводилось на базе МОУ «Средняя общеобразовательная школа № 10» г. Кунгура в ...
... сформировать более высокий уровень абстракции и обобщения, чем тот, на который ориентировалось традиционное преподавание»[4]. Следовательно, традиционные формы обучения не в состоянии поднять математическое мышление младших школьников на более высокий уровень. Как же решает эту проблему нетрадиционное обучение? Какие свойства математического мышления развивает решение нестандартных задач? Во- ...
... направлены на его практическую реализацию. Таблица 1.2.1. Дифференциация обучения. Внешняя Внутренняя Самодифференцировка учащихся в соответствии с их уровнем обученности ( по решению задач различной сложности) Спецшколы Классы с углубленным Изучением математики учитель определяет уровень развития и ...
0 комментариев