Уровневое тестирование

3.2 Уровневое тестирование

Одним из наиболее эффективных и удобных методов уровневой диагностики математических знаний, умений и навыков по сравнению с традиционными видами контроля (зачеты, опросы, устные контрольные работы и др.) являются тесты.

Тест состоит из нескольких коротких задач (вопросов), на которые учащийся должен реагировать или составлением ответа (что часто представляет собой заполнение пробелов), или комбинированием предложенных ему готовых ответов (выбор правильного ответа, объединение подходящих элементов, суждение о правильности представленных ответов и т.д.), а чаще всего включает в себя образец правильного решения каждой задачи (эталон).

Чтобы правильно составить тест для контроля уровня усвоения математического содержания, нужно знать основные требования, предъявляемые к предметным тестам: 1) функциональная валидность - соответствие проверяемому уровню усвоения; 2) содержательная валидность - соответствие содержанию проверяемого материала; 3) простота - включение в тест задач одного уровня, проверяющих усвоение одного факта или одного действия, 4) определенность - обеспечение общепонятности формулировок задач для всех учащихся; 5) однозначность - создание эталона, соответствующего полному и правильному решению задач.

Приведем примеры уровневых тестов различных видов, которые соответствуют типологии В. П. Беспалько.

Тесты 1 уровня. Они нацелены на выявление: 1) умение выполнять действие "подведения под понятие" при внешне заданных правилах действования ("с подсказкой"); 2) умения отличать правильное использование знания от неправильного. Тесты этого уровня должны требовать от ученика выполнение деятельности по узнаванию.

1. Тест опознания:

Является ли последовательность арифметической прогрессией: 1) 3; 6; 9; 12; ... ; 2) 2; 4; 8, 16; ...; 3) 10; 7; 4; 1; ...; 4) 100; 10; 1; 0,1; ...

Эталон: 1) - да; 2) - нет; 3) - да, 4) - нет.

2. Тест на различение:

Укажите арифметические прогрессии, разность которых равна 3: 1) 3; 6; 9; 12; ...; 2) 3, 0; –3; –6;...; 3) 1; 3; 9; 27;...; 4) –5; –2; 1; 4; ...

Эталон: 1) - да; 2) - нет; 3) - нет; 4) - да.

3. Тест на классификацию:

Укажите, какая из предложенных последовательностей является; а) арифметической прогрессией; б) геометрической прогрессией: 1) 3; 9; 27; …; 2) 1; 0,1; 0,01; …; 3) –40; –20; 0; …; 4) 23; 17,2; 11,4; …; 5) 8; 8; 8; …

Эталон: 1)- б); 2) - б); 3) -а); 4) -а); 5) -а) и -б).

4. Тест с пробелами:

Известны два члена арифметической прогрессии. Дополните неизвестный член прогрессии: 1) 4; 10; …; 2) 8; 5; …; 3) 3; …; 13; 4) 40; …;10; 5) …; 5; 9; 6) …; 10; 6.

Эталон: 1) - 16; 2) - 2; 3) - 8; 4) - 25; 5) - 1; 6) -14.

5. Математический диктант:

Учащиеся на слух воспринимают формулировки определений, теорем, фактов, формул и т. п. и определяют верно или неверно приведена учителем формулировка, ответ фиксируют в тетради в виде символов: "" - верно, "_" - неверно.

Верна или нет формулировка:

1) Две прямые называются параллельными, если они не пересекаются.

2) Два отрезка называются параллельными, если они не имеют общих точек.

3) Два луча называются параллельными, если они лежат на параллельных прямых.

4) Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.

5) Если при пересечении двух прямых третьей односторонние углы равны, то прямые параллельны.

Тесты 2 уровня. Они нацелены на выявление: 1) умения воспроизводить математическое содержание по памяти; 2) умения решать типовые задачи самостоятельно, воспроизводя по памяти способ решения.

1. Тест - подстановка:

Запишите формулы, которые надо использовать при решении следующих задач:

1) Найдите сумму десяти членов арифметической прогрессии, если a₁ = 5, a₁₀= 50.

2) Найдите сумму двадцати членов арифметической прогрессии: –23, –20.

3) В арифметической прогрессии a₁ = 20; d = 5. Найдите двадцатый ее член.

4) В арифметической прогрессии a₄ = 1,7; a₆ = 3,2. Найдите a₅.

5) Какой номер имеет член арифметической прогрессии, равный - 21, если первый член прогрессии равен 4, а равность рана 3.

2. Конструктивный тест:

1) Напишите формулу для нахождения двадцатого члена арифметической прогрессии.

Эталон: a₂₀ = a₁+19d.

2) Известны шестой и седьмой члены арифметической прогрессии. Напишите формулу, с помощью которой можно найти разность.

Эталон: d = a₇ – a₆.

3. Типовая задача.

Любая задача, взятая из обязательных результатов обучения.

Тесты 3 уровня. Нацелены на выявление: 1) умения воспроизводить и преобразовывать усвоенную информацию; 2) умения применять усвоенные способы решения типовых задач в нетипичной ситуации, но отчасти знакомой ученику.

Похожие работы

Развитие математических способностей учащихся в процессе внеклассной работы по математике в начальной школе

Скачать

210505

4

8

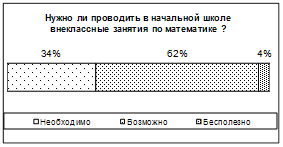
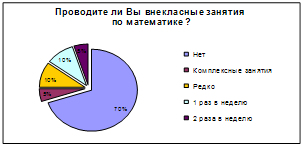
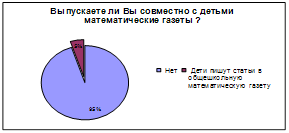
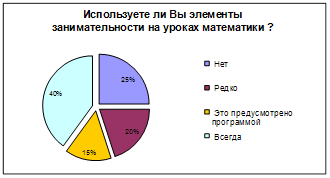
... и младших школьников. Анкета для студентов включала в себя два вопроса, один из которых о том, в чем, по их мнению, заключается развитие математических способностей школьников, а второй ¾ для выяснения отношения студентов к проведению внеклассной работы по математике в начальных классах. Анкета для преподавателей имела своей целью выяснить, проводят ли (а если проводят, то как часто) учителя ...

Развитие логического мышления на уроках математики при решении текстовых задач в 6 классе

Скачать

67022

2

2

... и перенести полученные знания на практику.   Глава 2. Работа учителя по развитию логического мышления на уроках математики   2.1 Опытно-экспериментальная работа и анализ ее результатов Опытно-экспериментальное исследование по выявлению уровня развития логического мышления школьников при решении текстовых задач проводилось на базе МОУ «Средняя общеобразовательная школа № 10» г. Кунгура в ...

Математическое мышление младших школьников

Скачать

88664

3

2

... сформировать более высокий уровень абстракции и обобщения, чем тот, на который ориентировалось традиционное преподавание»[4]. Следовательно, традиционные формы обучения не в состоянии поднять математическое мышление младших школьников на более высокий уровень. Как же решает эту проблему нетрадиционное обучение? Какие свойства математического мышления развивает решение нестандартных задач? Во- ...

Методические основы уровневой дифференциации при обучении алгебре в классах с углубленным изучением математики

Скачать

104362

23

0

... направлены на его практическую реализацию. Таблица 1.2.1. Дифференциация обучения.   Внешняя Внутренняя Самодифференцировка учащихся в соответст­вии с их уровнем обученности ( по решению задач различной слож­ности) Спецшколы Классы с углубленным Изучением математики учитель определяет уровень развития и ...