Навигация
Х=b/2; при b=4 нет решений
12560
знаков
0
таблиц
7
изображений
4 х=b/2; при b=4 нет решений. Пример 3. При каких а уравнение 
имеет единственное решение?
Сразу хочу обратить внимание на распространенную ошибку – считать данное уравнение квадратным. На самом деле это уравнение степени не выше второй! При а – 2=0, а = 2, уравнение вырождается в линейное имеет единственный корень х=1/4. Если же а2, то мы действительно имеем дело с квадратным уравнением, которое даёт единственное решение при D=0 
, 
, а=1, а=6.
Ответ: при а=2, а=1, а=6.
1.1 Решение уравнений первой степени с одним неизвестным
Решить такое уравнение – это значит:
1) определить множество допустимых значений неизвестного и параметров;
2) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнений.
Простейшее уравнение первой степени с одним неизвестным имеет вид ах-b=0.
При 
уравнение имеет единственное решение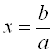 
, которое будет: положительным, ес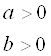ли 
или 
; нулевым, если 
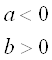; отрицательным, если 
или 
.
Если а=0, то при b=0 бесчисленное множество решений, а при b0 решений нет.
Пример 1. Для каждого значения а решить уравнение 
; найти при каких а корни больше нуля.
Это уравнение не является линейным уравнением (т.е. представляет собой дробь), но при х-1 и х0 сводится к таковому: 
или а-1-х=0.
Мы уже выявили допустимые значения икс (х-1 и х0), выявим теперь допустимые значения параметра а:
а-1-х=0 
а=х+1
Из этого видно, что при х0 а1, а при х-1 а0.
Таким образом, при а1 и а0 х=а-1 и это корень больше нуля при а>1.
Ответ: при а<0 х=а-1; при 
решений нет, а при a>1 корни положительны.
Пример 2. Решить уравнение 
(1).
Допустимыми значениями k и x будут значения, при которых 
.
Приведём уравнение к простейшему виду:
9х-3k=kx-12
(9 – k)x =3k-12 (2)
Найдём k, при которых изначальное уравнение не имеет смысла:
Подставив в (2) 
, получим:
.
Если подставим 
, то получим так же 
.
Таким образом, при уравнение (1) не имеет числового смысла, т.е. - это недопустимые значения параметра k для (1). При мы можем решать только уравнение (2).
1. Если 
, то уравнение (2) и вместе с ним уравнение (1) имеют единственное решение 
, которое будет:
а) положительным, если 
, при 4<k<9, с учётом 
: 
;
б) нулевым, если 
;
в) отрицательным, если 
и k>9 с учётом
, получаем 
.
2. Если 
, то уравнение (2) решений не имеет.
Ответ: а) при и 
, причём х>0 для 
; x=0 при k=4; x<0 при 
;
б) при 
уравнение не имеет решений.
Похожие работы
... точек координатной оси. Занятие № 4. Тема: Аналитический метод. Метод «ветвлений». Цель занятия: познакомить учеников с основным методом решения уравнений, содержащих параметр. Литература для учителя: см. [1] , [5], [6], [7], [14] Литература для ученика: см. [3] Краткое содержание: рассмотрение различных значений, принимаемых параметром. Упрощение уравнения и приведение уравнения к произведению ...
... знаменатель левой и правой его частей. После чего учащиеся решают известным им способом целое уравнение, исключая посторонние корни, т. е. числа, которые обращают общий знаменатель в нуль. В случае уравнений с параметрами эта задача более сложная. Здесь, чтобы исключить посторонние корни, требуется находить значение параметра, обращающее общий знаменатель в нуль, т. е. решать соответствующие ...
... функция является знакопостоянной. Вычисляя, например, , получаем, что функция принимает только положительные значения. Ответ. . Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих ...
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
0 комментариев