Алгоритм нечеткой кластеризации

1.3.5 Алгоритм нечеткой кластеризации

Четкая (непересекающаяся) кластеризация – кластеризация, которая каждый  из  относит только к одному кластеру.

Нечеткая кластеризация – кластеризация, при которой для каждого  из  определяется . – вещественное значение, показывающее степень принадлежности  к кластеру j.

Алгоритм нечеткой кластеризации таков:

1. Выбрать начальное нечеткое разбиение объектов на n кластеров путем выбора матрицы принадлежности  размера . Обычно .

2. Используя матрицу U, найти значение критерия нечеткой ошибки. Например,

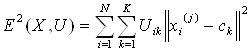, (1.2)

где - «центр масс» нечеткого кластера k,

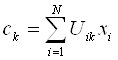. (1.3)

3. Перегруппировать объекты с целью уменьшения этого значения критерия нечеткой ошибки.

4. Возвращаться в пункт 2 до тех пор, пока изменения матрицы  не станут значительными.

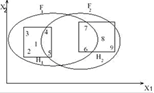
Рисунок 1.10 – Пример алгоритма нечеткой кластеризации

1.3.6 Применение нейронных сетей

Порой для решения задач кластеризации целесообразно использовать нейронные сети. У данного подхода есть ряд особенностей:

· искусственные нейронные сети легко работают в распределенных системах с большой параллелизацией в силу своей природы;

· поскольку искусственные нейронные сети подстраивают свои весовые коэффициенты, основываясь на исходных данных, это помогает сделать выбор значимых характеристик менее субъективным.

Существует масса ИНС, например, персептрон, радиально-базисные сети, LVQ-сети, самоорганизующиеся карты Кохонена, которые можно использовать для решения задачи кластеризации. Но наиболее лучше себя зарекомендовала сеть с применением самоорганизующихся карт Кохонена, которая и выбрана для рассмотрения в данном дипломном проекте.

1.3.7  Генетические алгоритмы

Это алгоритм, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений. Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе.

Задача формализуется таким образом, чтобы её решение могло быть закодировано в виде вектора («генотипа») генов. Где каждый ген может быть битом, числом или неким другим объектом. В классических реализациях ГА предполагается, что генотип имеет фиксированную длину. Однако существуют вариации ГА, свободные от этого ограничения.

Общая схема данного подхода:

1. Выбрать начальную случайную популяцию множества решений и получить оценку качества для каждого решения (обычно она пропорциональна ).

2. Создать и оценить следующую популяцию решений, используя эволюционные операторы: оператор выбора – с большой вероятностью предпочитает хорошие решения; оператор рекомбинации (обычно это «кроссовер») – создает новое решение на основе рекомбинации из существующих; оператор мутации – создает новое решение на основе случайного незначительного изменения одного из существующих решений.

3. Повторять шаг 2 до получения нужного результата.

Главным достоинством генетических алгоритмов в данном применении является то, что они ищут глобальное оптимальное решение. Большинство популярных алгоритмов оптимизации выбирают начальное решение, которое затем изменяется в ту или иную сторону. Таким образом получается хорошее разбиение, но не всегда самое оптимальное. Операторы рекомбинации и мутации позволяют получить решения, сильно не похожее на исходное – таким образом осуществляется глобальный поиск.

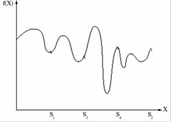
Рисунок 1.11 – Пример генетического алгоритма