Навигация
Выбор начальных значений векторов весовых коэффициентов и нейронов
3. Выбор начальных значений векторов весовых коэффициентов и нейронов.
Если начальные значения выбраны неудачно, т. е. расположенными далеко от предъявляемых входных векторов, то нейрон не окажется победителем ни при каких входных сигналах, а, следовательно, не обучится.
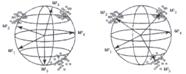
На рисунке 2.12 показан случай, когда начальное расположение весов ![]() и
и ![]() привело к тому, что после обучения сети все предъявляемые образы классифицируют нейроны с весами
привело к тому, что после обучения сети все предъявляемые образы классифицируют нейроны с весами ![]() ,
, ![]() , и
, и ![]() . Веса же
. Веса же ![]() и
и ![]() не изменились и могут быть удалены из сети.
не изменились и могут быть удалены из сети.
а б
Рисунок 2.12 – Начальное (а) и конечное (б) положения векторов весов
4. Выбор параметра расстояния ![]()
Если сначала параметр ![]() выбран малым или очень быстро уменьшается, то далеко расположенные друг от друга нейроны не могут влиять друг на друга. Хотя две части в такой карте настраиваются правильно, общая карта будет иметь топологический дефект (рисунок 2.13).
выбран малым или очень быстро уменьшается, то далеко расположенные друг от друга нейроны не могут влиять друг на друга. Хотя две части в такой карте настраиваются правильно, общая карта будет иметь топологический дефект (рисунок 2.13).
5. Количество нейронов в слое
Число нейронов в слое Кохонена должно соответствовать числу классов входных сигналов. Это может быть недопустимо в тех задачах, когда число классов заранее известно.

Рисунок 2.13 – Топологический дефект карты
6. Классы входных сигналов
Слой Кохонена может формировать только классы, представляющие собой выпуклые области входного пространства.
2.5 Задачи, решаемые при помощи карт КохоненаСамоорганизующиеся карты могут использоваться для решения задач моделирования, прогнозирования, кластеризации, поиска закономерностей в больших массивах данных, выявления наборов независимых признаков и сжатии информации.
Наиболее распространенное применение сетей Кохонена - решение задачи классификации без учителя, т.е. кластеризации.
Напомним, что при такой постановке задачи нам дан набор объектов, каждому из которых сопоставлена строка таблицы (вектор значений признаков). Требуется разбить исходное множество на классы, т.е. для каждого объекта найти класс, к которому он принадлежит.
В результате получения новой информации о классах возможна коррекция существующих правил классификации объектов.
Самым распространенным применением карт Кохонена является:
· разведочный анализ данных
· обнаружение новых явлений
В первом случае сеть Кохонена способна распознавать кластеры в данных, а также устанавливать близость классов. Таким образом, пользователь может улучшить свое понимание структуры данных, чтобы затем уточнить нейросетевую модель. Если в данных распознаны классы, то их можно обозначить, после чего сеть сможет решать задачи классификации. Сети Кохонена можно использовать и в тех задачах классификации, где классы уже заданы, - тогда преимущество будет в том, что сеть сможет выявить сходство между различными классами.
Во втором случае сеть Кохонена распознает кластеры в обучающих данных и относит все данные к тем или иным кластерам. Если после этого сеть встретится с набором данных, непохожим ни на один из известных образцов, то она не сможет классифицировать такой набор и тем самым выявит его новизну.
кластеризация нейронный сеть кохонен
3. МОДЕЛИРОВАНИЕ СЕТИ КЛАСТЕРИЗАЦИИ ДАННЫХ В MATLAB NEURAL NETWORK TOOLBOX
Программное обеспечение, позволяющее работать с картами Кохонена, сейчас представлено множеством инструментов. Это могут быть как инструменты, включающие только реализацию метода самоорганизующихся карт, так и нейропакеты с целым набором структур нейронных сетей, среди которых - и карты Кохонена; также данный метод реализован в некоторых универсальных инструментах анализа данных.
К инструментарию, включающему реализацию метода карт Кохонена, относятся MATLAB Neural Network Toolbox, SoMine, Statistica, NeuroShell, NeuroScalp, Deductor и множество других.
3.1 Самоорганизующиеся нейронные сети в MATLAB NNT
Для создания самоорганизующихся нейронных сетей, являющихся слоем или картой Кохонена, предназначены М-функции newc и newsom cooтветственно.
По команде help selforg можно получить следующую информацию об М-функциях, входящих в состав ППП Neural Network Toolbox и относящихся к построению сетей Кохонена (таблица 3.1):
Таблица 3.1
М-функции, входящие в состав ППП Neural Network Toolbox
| Self-organizing networks | Самоорганизующиеся сети |
| New networks | Формирование сети |
| newc newsom | Создание слоя Кохонена Создание карты Кохонена |
| Using networks | Работа с сетью |
| sim init adapt train | Моделирование Инициализация Адаптация Обучение |
| Weight functions | Функции расстояния и взвешивания |
| negdist | Отрицательное евклидово расстояние |
| Net input functons | Функции накопления |
| netsum | Сумма взвешенных входов |
| Transfer functions | Функции активации |
| compet | Конкурирующая функция активации |
| Topology functions | Функции описания топологии сети |
| gridtop hextop randtop | Прямоугольная сетка Гексагональная сетка Сетка со случайно распределенными узлами |
| Distance functions | Функции расстояния |
| dist boxdist mandist linkdist | Евклидово расстояние Расстояние максимального координатного смещения Расстояние суммарного координатного смешения Расстояние связи |
| Initialization functions | Функции инициализации сети |
| initlay initwb initcon midpoint | Послойная инициализация Инициализация весов и смещений Инициализация смещений с учетом чувствительности нейронов Инициализация весов по правилу средней точки |
| Learning functions | функции настройки параметров |
| learnk learncon learnsom | Правило настройки весов для слоя Кохонена Правило настройки смещений для слоя Кохонена Правило настройки весов карты Кохонена |
| Adapt functions | Функции адаптации |
| adaptwb | Адаптация весов и смещений |
| Training functions | Функции обучения |
| trainwb1 | Повекторное обучение весов и смещений |
| Demonstrations | Демонстрационные примеры |
| democ1 demosm1 demosm2 | Настройка слоя Кохонена Одномерная карта Кохонена Двумерная карта Кохонена |
0 комментариев