Моделирование кластеризации данных

3.1.6 Моделирование кластеризации данных

Функционирование слоя Кохонена можно пояснить более наглядно, используя графику системы MATLAB. Рассмотрим 48 случайных векторов на плоскости, формирующих 8 кластеров, группирующихся около своих центров. На графике, приведенном на рисунке 3.3, показано 48 двухэлементных векторов входа.

Сформируем координаты случайных точек и построим план их расположения на плоскости:

с = 8

n = 6 % Число кластеров, векторов в кластере

d = 0.5 % Среднеквадратичное отклонение от центра кластера

х = [-10 10;-5 5] % Диапазон входных значений

[r,q] = size(x); minv = min(x1)1; maxv = mах(х1)1

v = rand(r, e).С{maxv - minv) *ones(l,c) + xninv*ones (l,c) )t = c*n % Число точек

v= [v v v v v]; v=v+randn{r,t)*d % Координаты точек

Р = v

plot(P(l,:), P(2,:),'+k') % (рисунок 3.3)

title('Векторы входа'), xlabel('Р(1,:)'), ylabel('P(2,:)').

Векторы входа, показанные на рисунке 3.3, относятся к различным классам.

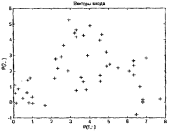
Рисунок 3.3 – Двухэлементные векторы входа

Применим конкурирующую сеть из восьми нейронов для того, чтобы распределить их по классам:

net = newc([-2 12;-1 6], 8 ,0.1)

w0 =net.IW{l}

b0 = net.b{l}

c0 = exp(l)./b0.

Начальные значения весов, смещений и параметров активности нейронов представлены ниже:

w0 =b0 =с0 =

0.50.2521.7460.125

0.50.2521,7460.125

0.50.2521.7460.125

0-50.2521.7460.125

0.50.2521.7460.125

0.50.2521.7460.125

0.50.2521.7460.125

0.50.2521.7460.125.

После обучения в течение 500 циклов получим:

net.trainParam.epochs = 500

net = train(net,P)

w = net.IW{l} bn = net.b{l}

cn = exp(1)./bn

wn=bn=cn=

6.2184 2.423922.1370,123

1.3277 0.9470121.7180.125

0.31139 0.4093521.1920.128

3.543 4.584521.4720.127

3.4617 2.8S9621.9570.124

4 3171 1.427821.1850.128

6.7065 0.4369623.0060.118

0.97S17 0.1724221.420.127.

Как следует из приведенных таблиц, центры кластеризации распределились по восьми областям, показанным на рисунке 3.4, а; смещения отклонились в обе стороны от исходного значения 21.746 также, как и параметры активности нейронов, показанные на рисунке 3.4, б.

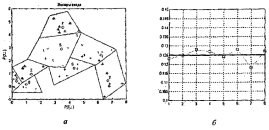
Рисунок 3.4 – Полученные центры кластеризации

Рассмотренная самонастраивающаяся сеть Кохонена является типичным примером сети, которая реализует процедуру обучения без учителя.

3.2 Карта Кохонена в MATLAB NNT

Самоорганизующаяся сеть в виде карты Кохонена предназначена для решения задач кластеризации входных векторов. В отличие от слоя Коконена карта Кохонена поддерживает такое топологическое свойство, когда близким кластерам входных векторов соответствуют близко расположенные нейроны.

Первоначальная топология размещения нейронов в слое Кохонена задается М-функциями gridtop, hextop или randtop, что соответствует размещению нейронов в узлах либо прямоугольной, либо гексагональной сетки, либо в узлах сетки со случайной топологией. Расстояния между нейронами вычисляются с помощью специальных функций вычисления расстояний dist, boxdist, linkdist и mandist.

Карта Кохонена для определения нейрона-победителя использует ту же процедуру, какая применяется и в слое Кохонена. Однако на карте Кохонена одновременно изменяются весовые коэффициенты соседних нейронов в соответствии со следующим соотношением:

. (3.7)

В этом случае окрестность нейрона-победителя включает все нейроны, которые находятся в пределах некоторого радиуса :

.  (3.8)

Чтобы пояснить понятие окрестности нейрона, обратимся к рисунку 3.5.

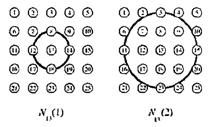
Рисунок 3.5 – Окрестности нейрона

Левая часть рисунка соответствует окрестности радиуса 1 для нейрона-победителя с номером 13; правая часть - окрестности радиуса 2 для того же нейрона. Описания этих окрестностей выглядят следующим образом:

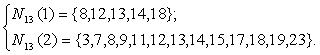
Заметим, что топология карты расположения нейронов не обязательно должна быть двумерной. Это могут быть и одномерные и трехмерные карты, и даже карты больших размерностей. В случае одномерной карты Кохонена, когда нейроны расположены вдоль линии, каждый нейрон будет иметь только двух соседей в пределах радиуса 1 или единственного соседа, если нейрон расположен на конце линии. Расстояния между нейронами можно определять различными способами, используя прямоугольные или гексагональные сетки, однако это никак не влияет на характеристики сети, связанные с классификацией входных векторов.

3.2.1 Топология карты

Как уже отмечалось выше, можно задать различные топологии для карты расположения нейронов, используя М-функции gridtop, hextop, randtop.

Рассмотрим простейшую прямоугольную сетку размера 2x3 для размещения шести нейронов, которая может быть сформирована с помощью функции gridtop:

pos = gridtop(2,3)

pos =

0 1 0 1 0 1

0 0 1 1 2 2

plotsom(pos) % (рисунок 3.6).

Соответствующая сетка показана на рисунке 3.6. Метки position(1, i) и position(2,i) вдоль координатных осей генерируются функцией plotsom и задают позиции расположения нейронов по первой, второй и т. д. размерностям карты.

Рисунок 3.6 – Прямоугольная сетка

Здесь нейрон 1 расположен в точке с координатами (0,0), нейрон 2 - в точке (1,0), нейрон 3 - в точке (0,1) и т. д. Заметим, что, если применить команду gridtop, переставив аргументы местами, получим иное размещение нейронов;

pos=gridtop(3,2)pos =

0 1 2 0 1 2

0 0 0 1 1 1.

Гексагональную сетку можно сформировать с помощью функции hextop:

pos = hextop(2,3)

pos =

0 1.0000 0.5000 1.5000 0 1.0000

0 0 0.8660 0.8660 1.7321 1.7321.

plotsom (pos) % (рисунок 3.7).

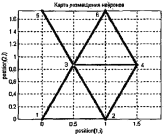
Рисунок 3.7 – Гексагональная сетка

Заметим, что М-функция hextop используется по умолчанию при создании карт Кохонена при применении функции newsom.

Сетка со случайным расположением узлов может быть создана с помощью функции randtop:

pos = randtop(2,3)

pos =

0.061787 0.64701 0.40855 0.94383 0 0.65113

0 0.12233 0.90438 0.54745 1.4015 1.5682

plotsom(pos) % (рисунок 3.8).

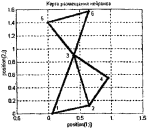
Рисунок 3.8 – Сетка со случайным расположением узлов

3.2.2 Функции для расчета расстояний

В ППП NNT используется 4 функции для расчета расстояний между узлами сетки.

Функция dist вычисляет евклидово расстояние между нейронами, размещенными в узлах сетки, в соответствии с формулой:

, (3.9)

где ,  - векторы положения нейронов с номерами i и j.

Обратимся к прямоугольной сетке из шести нейронов (рисунок 3.6) и вычислим соответствующий массив расстояний:

pos = gridtop(2,3)

d = disе(pos)

d =

0 1 1 1.4142 2 2.2361

1 0 1.4142 1 2.2361 2

1 1.4142 0 1 1 1.4142

1.4142 1 1 0 1.4142 1

2 2.2361 1 1.4142 0 1

2.2361 2 1.4142 1 1 0.

Этот массив размера 6х6 описывает расстояния между нейронами и содержит на диагонали нули, поскольку они определяют расстояние нейрона до самого себя, а затем, двигаясь вдоль строки, до второго, третьего и т. д.

На рисунке 3.9 показано расположение нейронов в узлах прямоугольной сетки. Введем понятие окрестности для прямоугольной сетки. В этом случае окрестность размера 1, или просто окрестность 1, включает базовый нейрон и его непосредственных соседей; окрестность 2 включает нейроны из окрестности 1 и их соседей.

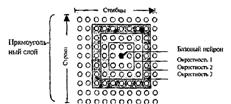
Рисунок 3.9 – Расположение нейронов в узлах прямоугольной сетки

Размер, а соответственно и номер окрестности, определяется максимальным значением координаты смещения нейрона от базового. Вводимое таким способом расстояние между нейронами называется расстоянием максимального координатного смещения и может быть вычислено по формуле:

, (3.10)

где ,  - векторы положения нейронов с номерами i и j.

Для вычисления этого расстояния в ППП NNT предназначена М-функция boxdist. Для конфигурации нейронов, показанной на рисунке 3.6, эти расстояния равны:

роs = gridtop(2,3)

d = boxdist(pos)

d=

0 1 1 1 2 2

1 0 1 1 2 2

1 1 0 1 1 1

1 1 1 0 1 1

2 2 1 1 0 1

2 2 1 1 1 0.

Расстояние максимального координатного смещения между базовым нейроном 1 и нейронами 2, 3 и 4 равно 1, поскольку они находятся в окрестности 1, а расстояние между базовым нейроном и нейронами 5 и 6 равно 2, и они находятся в окрестности 2. Расстояние максимального координатного смещения от нейронов 3 и 4 до всех других нейронов равно 1.

Определим другое расстояние между нейронами, которое учитывает то количество связей, которое необходимо установить, чтобы задать путь движения от базового нейрона. Если задано  нейронов, положение которых определяется векторами , i = 1,..., S, то расстояние связи между ними определяется соотношением:

 (3.11)

Если евклидово расстояние между нейронами меньше или равно 1, то расстояние связи принимается равным 1; если между нейронами с номерами i и j имеется единственный промежуточный нейрон с номером , то расстояние связи равно 2, и т. д.

Для вычисления расстояния связи в ППП NNT предназначена функции linkdist. Для конфигурации нейронов, доказанной на рисунке 3.6, эти расстояния равны:

pos = gridtop{2,3)

d = linkdist(pos)

d =

0 1 1 2 2 3

1 0 2 1 3 2

1 2 0 1 1 2

2 1 1 0 2 1

2 3 1 2 0 1

3 2 2 1 1 0.

Расстояние связи между базовым нейроном 1 и нейронами 2, 3 равно 1, между базовым нейроном и нейронами 4 и 5 равно 2, между базовым нейроном и нейроном 6 равно 3. Наконец, определим расстояние максимального координатного смещении по формуле:

, (3.12)

где , - векторы расположения нейронов с номерами i и j.

Для вычисления расстояния максимального координатного смещения в ППП NNT предназначена функции mandist.

Вновь обратимся к конфигурации нейронов на рисунке 3.6:

pos = gridtop(2,3)

d = mandist(pos)

d =

0 1 1 2 2 3

1 0 2 1 3 2

1 2 0 1 1 2

2 1 1 0 2 1

2 3 1 2 0 1

3 2 2 1 1 0.

В случае прямоугольной сетки оно совпадает с расстоянием связи.

3.2.3 Архитектура сети

Промоделированная архитектура самоорганизующейся карты Кохонена в MATLAB NNT показана на рисунке 3.10.

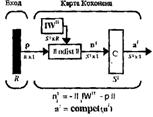
Рисунок 3.10 – Архитектура самоорганизующейся карты Кохонена

Эта архитектура аналогична структуре слоя Кохонена за исключением того, что здесь не используются смещения. Конкурирующая функция активации возвращает 1 для элемента выхода , соответствующего победившему нейрону; все другие элементы вектора  равны 0.

Однако в сети Кохонена выполняется перераспределение нейронов, соседствующих с победившим нейроном. При этом можно выбирать различные топологии размещения нейронов и различные меры для вычисления расстояний между нейронами.