Навигация
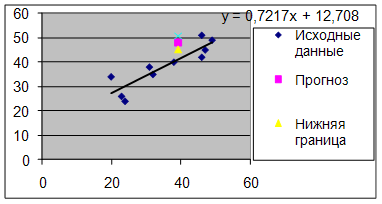
Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05)
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).
![]()
![]()
![]()
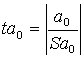 ;
;
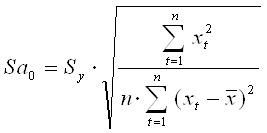
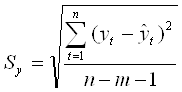
![]()
| x | y |
|
|
|
|
|
| 17 | 26 | 289 | 24,718 | 1,282 | 1,6435 | 13,69 |
| 22 | 27 | 484 | 28,523 | -1,523 | 2,3195 | 75,69 |
| 10 | 22 | 100 | 19,391 | 2,609 | 6,8069 | 1,89 |
| 7 | 19 | 49 | 17,108 | 1,892 | 3,5797 | 39,9 |
| 12 | 21 | 144 | 20,913 | 0,087 | 0,0076 | 1,69 |
| 21 | 26 | 441 | 27,762 | -1,762 | 3,1046 | 59,29 |
| 14 | 20 | 196 | 22,435 | -2,435 | 5,9292 | 0,49 |
| 7 | 15 | 49 | 17,108 | -2,108 | 4,4437 | 39,69 |
| 20 | 30 | 400 | 27,001 | 2,999 | 8,9940 | 44,89 |
| 3 | 13 | 9 | 14,064 | -1,064 | 1,1321 | 106,09 |
| 133 | 219 | 2161 | * | -0,023 | 37,9608 | 392,1 |
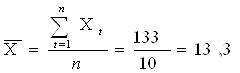
![]()
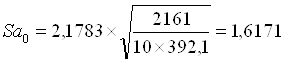
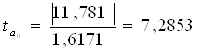
![]()
![]()
![]()
![]() , следовательно, параметр
, следовательно, параметр ![]() значим.
значим.
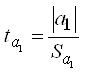

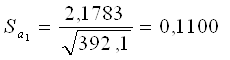
![]()
![]()
![]()
![]() , следовательно, коэффициент регрессии
, следовательно, коэффициент регрессии ![]() значим.
значим.
Интервальная оценка:
![]()
![]()
![]()
![]()
а0: 11,781![]() 2,31*1,617
2,31*1,617
а0: 11,781![]() 3,735
3,735
Нижняя граница: 11,781-3,735=8,046
Верхняя граница: 11,781+3,735=15,516
а0: (8,046![]() 15,516), следовательно, параметр а0 значим, так как в эти границы не попадает 0.
15,516), следовательно, параметр а0 значим, так как в эти границы не попадает 0.
![]()
![]()
а1: 0,761![]() 2,31*0,11
2,31*0,11
а1: 0,761![]() 0,2541
0,2541
Нижняя граница: 0,761-0,254=0,507
Верхняя граница: 0,761+0,254=1,015
а1: (0,507![]() 1,015), следовательно, коэффициент регрессии а1 значим, так как в эти границы не попадает 0.
1,015), следовательно, коэффициент регрессии а1 значим, так как в эти границы не попадает 0.
5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Для нахождения коэффициента детерминации найдём коэффициент парной корреляции:
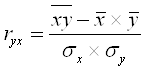
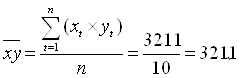
![]()
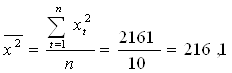
![]()
![]()

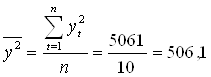
![]()
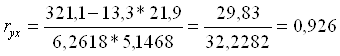
Проверяем значимость ![]() по критерию Стьюдента:
по критерию Стьюдента:
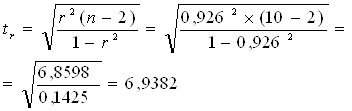
![]()
![]()
![]()
![]() , следовательно,
, следовательно, ![]() значим.
значим.
![]() =0,926, то есть связь между переменными y и x очень тесная (то есть близко к 1) и прямая (так как больше 0).
=0,926, то есть связь между переменными y и x очень тесная (то есть близко к 1) и прямая (так как больше 0).
Находим коэффициент детерминации:
![]() , то есть 85,8% - изменение объёма выпуска продукции (зависимой переменной «y») происходит под влиянием объёма капиталовложений (фактора «х», включённого в модель).
, то есть 85,8% - изменение объёма выпуска продукции (зависимой переменной «y») происходит под влиянием объёма капиталовложений (фактора «х», включённого в модель).
Значимость уравнения регрессии по критерию Фишера:
![]()
![]()
![]()
![]()
![]() , следовательно, уравнение регрессии значимо, модель адекватна.
, следовательно, уравнение регрессии значимо, модель адекватна.
Средняя относительная ошибка аппроксимации:
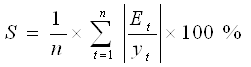
| x | y |
|
|
|
| 17 | 26 | 24,718 | 1,282 | 0,0493 |
| 22 | 27 | 28,523 | -1,523 | 0,0564 |
| 10 | 22 | 19,391 | 2,609 | 0,1186 |
| 7 | 19 | 17,108 | 1,892 | 0,0996 |
| 12 | 21 | 20,913 | 0,087 | 0,0041 |
| 21 | 26 | 27,762 | -1,762 | 0,0678 |
| 14 | 20 | 22,435 | -2,435 | 0,1218 |
| 7 | 15 | 17,108 | -2,108 | 0,1405 |
| 20 | 30 | 27,001 | 2,999 | 0,1000 |
| 3 | 13 | 14,064 | -1,064 | 0,0818 |
| 133 | 219 | * | -0,023 | 0,7332 |
![]()
Так как ![]() , значит модель не достаточно точная.
, значит модель не достаточно точная.
F-критерий намного больше табличного значения, коэффициент детерминации ![]() очень близок к 1, а относительная ошибка аппроксимации составляет 7,33%. На основании рассчитанных критериев можно сделать вывод о хорошем качестве модели.
очень близок к 1, а относительная ошибка аппроксимации составляет 7,33%. На основании рассчитанных критериев можно сделать вывод о хорошем качестве модели.
6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора X составляет 80% от его максимального значения.
![]()
![]()
![]()
![]() - прогноз факторного признака (объема капиталовложений).
- прогноз факторного признака (объема капиталовложений).
![]() - точечный прогноз.
- точечный прогноз.
(17,6; 25,2) – точка должна лежать на графике модели.
Интервальный прогноз:
![]()
![]()
![]()
![]()

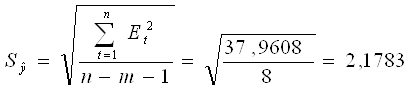
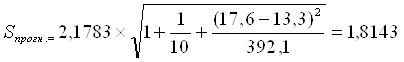
25,2![]() 1,86
1,86![]() 1,81
1,81
25,2![]() 3,37
3,37
Нижняя граница: 25,2-3,37=21,83
Верхняя граница: 25,2+3,37=28,57
То есть при уровне значимости ![]() =0,1, если прогнозное значение фактора «Х» составит 80% от его максимального значения или 17,6, точечный прогноз среднего значения «Y» по линейной модели составит 25,2. Доверительный интервал: 21,83
=0,1, если прогнозное значение фактора «Х» составит 80% от его максимального значения или 17,6, точечный прогноз среднего значения «Y» по линейной модели составит 25,2. Доверительный интервал: 21,83![]() 28,57.
28,57.
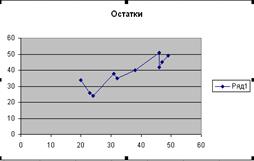
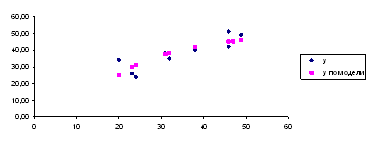
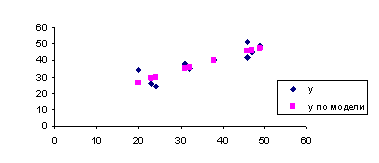
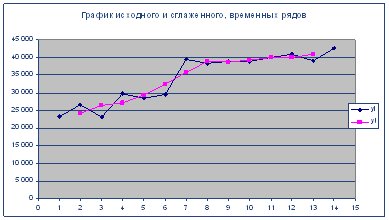
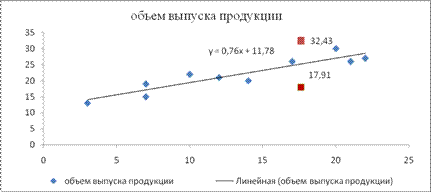
7. Представить графически фактические и модельные значения Y точки прогноза рис. 3.
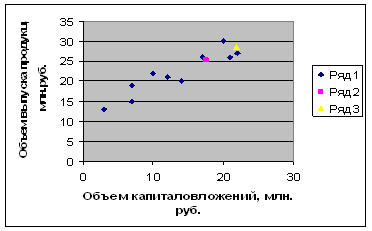
Рис. 3
8. Составить уравнения нелинейной регрессии:
· Гиперболической;
· Степенной;
· Показательной.
Привести графики построенных уравнений регрессии.
9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.
Уравнение степенной модели парной регрессии:
![]()
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведём логарифмирование обеих частей уравнения:
![]()
Обозначим ![]() ,
, ![]() ,
, ![]() . Тогда уравнение примет вид
. Тогда уравнение примет вид ![]() - линейное уравнение регрессии.
- линейное уравнение регрессии.
Рассчитаем его параметры (см. приложение).
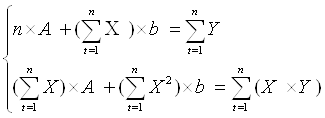
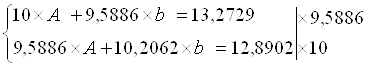
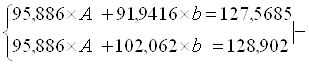
![]()
![]()
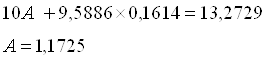
Получим уравнение степенной модели регрессии:
![]()
Построим график (рис. 4):
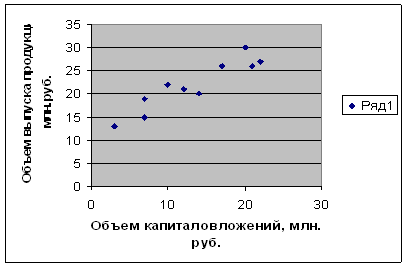
Рис. 4
Определим коэффициент корреляции:

Связь между показателем y и фактором x можно считать достаточно тесной.
Коэффициент детерминации:
![]()
Вариация результата Y (объёма выпуска продукции) на 57,5% объясняется вариацией фактора X (объёмом капиталовложений).
Средняя относительная ошибка аппроксимации:
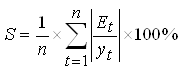
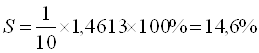
В среднем расчётные значения ![]() для степенной модели отличаются от фактических значений на 14,6%.
для степенной модели отличаются от фактических значений на 14,6%.
Коэффициент эластичности для степенной модели регрессии:
![]() , значит, если фактор X (объём капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится в среднем на 0,16%.
, значит, если фактор X (объём капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится в среднем на 0,16%.
Уравнение показательной модели парной регрессии:
![]()
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:
![]()
Обозначим ![]() ,
, ![]() ,
, ![]() . Тогда уравнение примет вид
. Тогда уравнение примет вид ![]() - линейное уравнение регрессии.
- линейное уравнение регрессии.
Рассчитаем его параметры.
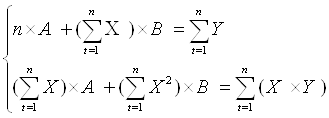
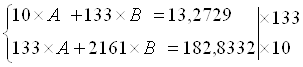
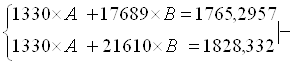
![]()
![]()
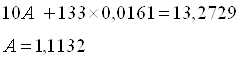
![]()
![]()
Перейдём к исходным переменным x и y.
![]()
Построим график (рис. 5):
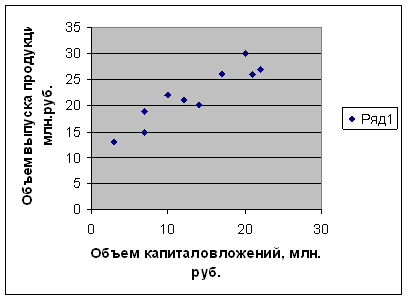
Рис. 5
Определим индекс корреляции:

Связь между показателем y и фактором x можно считать достаточно тесной.
Коэффициент детерминации:
![]()
Вариация результата Y (объёма выпуска продукции) на 82,9% объясняется вариацией фактора X (объёмом капиталовложений).
Средняя относительная ошибка аппроксимации:
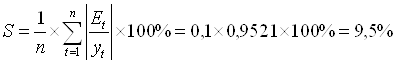
В среднем расчётные значения ![]() для степенной модели отличаются от фактических значений на 9,5%.
для степенной модели отличаются от фактических значений на 9,5%.
Коэффициент эластичности для показательной модели регрессии:
![]() , значит, если фактор X (объём капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится в среднем на 0,49%.
, значит, если фактор X (объём капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится в среднем на 0,49%.
Уравнение гиперболической модели парной регрессии:
![]()
Произведём линеаризацию модели путём замены ![]() .
.
В результате получим линейное уравнение:
![]()
Рассчитаем его параметры.
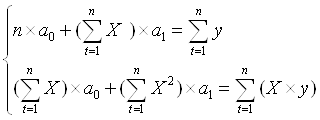
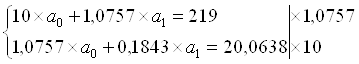
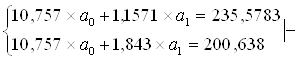
![]()
![]()
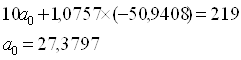
Получим следующее уравнение гиперболической модели:
![]()
Построим график (рис. 6):
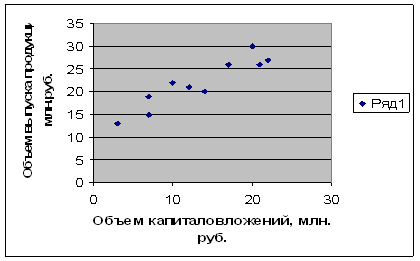
Рис. 6
Определим индекс корреляции:

Связь между показателем y и фактором x можно достаточно тесной.
Коэффициент детерминации:
![]()
Вариация результата Y (объёма выпуска продукции) на 67,2% объясняется вариацией фактора X (объёмом капиталовложений).
Средняя относительная ошибка аппроксимации:
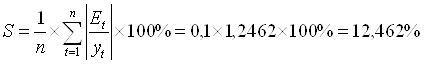
В среднем расчётные значения ![]() для степенной модели отличаются от фактических значений на 12,46%.
для степенной модели отличаются от фактических значений на 12,46%.
Коэффициент эластичности для гиперболической модели регрессии:
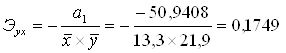 %, значит, если фактор X (объём капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится в среднем на 0,18%.
%, значит, если фактор X (объём капиталовложений) увеличить на 1%, то значение зависимой переменной Y (объём выпуска продукции) увеличится в среднем на 0,18%.
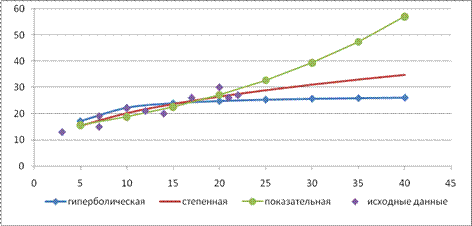
Сравним модели по коэффициенту детерминации, коэффициенту эластичности и средней относительной ошибке аппроксимации:
| Модель парной регрессии | Критерий | ||
| | | | |
| Степенная | 0,575 | 14,6% | 0,16% |
| Показательная | 0,829 | 9,5% | 0,49% |
| Гиперболическая | 0,672 | 12,5% | 0,18% |
Самое хорошее качество имеет показательная модель. Коэффициент детерминации наиболее близок к 1 (вариация объёма капиталовложений на 82,9% объясняет вариацию объёма выпуска продукции), наименьшая средняя относительная ошибка аппроксимации S=9,5% и среднее значение коэффициента эластичности ![]()
![]() .
.
Похожие работы
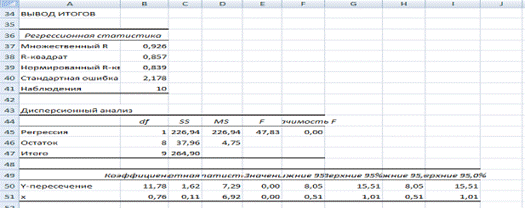
нты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод. Решение 1. Уравнение линейной регрессии имеет вид: = а0 + а1x. Построим линейную модель. Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка). ( ...
... 7,33 1965 81,0 7,52 1966 83,0 7,62 1967 85,4 7,72 1968 85,9 7,89 1969 85,9 7,98 1970 87,0 8,03 1971 90,2 8,21 1972 92,6 8,53 1973 95,0 8,55 1974 93,3 8,28 1975 95,5 8,12 Найдем параметры линейного уравнения множественной регрессии и значения остатков. Дополним таблицу данных столбцами "", "Квадрат разности остатков " и "Квадрат остатка " и заполним их. Таблица ...
... 106,09 14,97 1,97 3,88 1,53 2,34 сумма 133 219 3211 2161 264,90 392,1 24,43 106,37 0,26 78,80 ср. знач. 13,3 21,9 321,1 216,1 ; Уравнение линейной регрессии имеет вид: у=11,78+0,76х С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличится в среднем на 76 тыс. руб ...
... t-критерий Стъюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: Оценка значимости коэффициентов чистой регрессии с помощью /-критерия ...
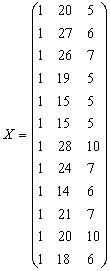

0 комментариев