Навигация
3. Расчет дисперсии опыта
Построчная дисперсия ![]() для каждого эксперимента определяется по формуле:
для каждого эксперимента определяется по формуле:
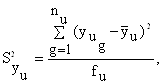 (1)
(1)
![]() (2)
(2)
где g и nu - номер и количество дублей эксперимента соответственно; ![]() - результат g-го повторения u-го эксперимента;
- результат g-го повторения u-го эксперимента; ![]() - среднее арифметическое значение всех дублей u - го эксперимента; fu - число степеней свободы в u - м опыте при определении u - й построчной дисперсии
- среднее арифметическое значение всех дублей u - го эксперимента; fu - число степеней свободы в u - м опыте при определении u - й построчной дисперсии ![]() .
.
Число степеней свободы – понятие, учитывающее в статистических ситуациях связи, ограничивающие свободу изменения случайных величин. Это число определяется как разность между числом выполненных опытов и числом констант (средних, коэффициентов и пр.), подсчитанных по результатам тех же опытов.
В нашем случае nu = 3, fu = 3 - 1 = 2. Тогда выражение (1) можно переписать следующим образом:
 (3)
(3)
Построчная дисперсия по выражению (3) рассчитывается для каждого u - го опыта отдельно. Результаты расчетов построчной дисперсии приведены в табл. 4.
Таблица 4
Результаты расчета построчной дисперсии
| Номер опыта, u | Номер дубля, g | Удельная потеря массы, | Среднее арифметическое значение интенсивности изнашивания, | Построчная дисперсия, |
| 1 | 1 | 97,8 | 97,3 | 5,975 |
| 2 | 99,4 | |||
| 3 | 94,6 | |||
| 2 | 1 | 128,3 | 127,6 | 8,245 |
| 2 | 130,0 | |||
| 3 | 124,4 | |||
| 3 | 1 | 152,1 | 153,7 | 27,93 |
| 2 | 149,4 | |||
| 3 | 159,6 | |||
| 4 | 1 | 73,8 | 71,9 | 2,77 |
| 2 | 71,2 | |||
| 3 | 70,7 | |||
| 5 | 1 | 110,3 | 113,7 | 18,43 |
| 2 | 118,5 | |||
| 3 | 112,2 | |||
| 6 | 1 | 93,8 | 91,8 | 3,225 |
| 2 | 91,1 | |||
| 3 | 90,4 | |||
| 7 | 1 | 126,2 | 127,1 | 8,17 |
| 2 | 130,3 | |||
| 3 | 124,8 | |||
| 8 | 1 | 114,2 | 112,2 | 3,665 |
| 2 | 110,4 | |||
| 3 | 111,9 |
регрессия дисперсия дублирование
Приведем пример расчета построчной дисперсии в первом опыте (u = 1):
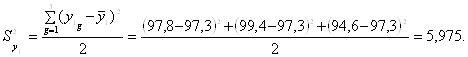
После определения построчных дисперсий производят проверку воспроизводимости экспериментальных данных. Проверка выполняется в том случае, если имеет место дублирование опытов, что является обязательным правилом при проведении планированного эксперимента. На этой стадии проверяется гипотеза о постоянстве дисперсии шума с использованием критерия Кохрена. Проверка данной гипотезы позволяет судить об однородности или неоднородности ряда дисперсий. Если ряд дисперсий однороден, различные значения функции отклика (y) определяются с одинаковой точностью. Если ряд дисперсий неоднороден, различные значения функции отклика (y) определяются с разной точностью.
Процедура проверки статистических гипотез в общем случае формально предусматривает сравнение некоторого критерия, рассчитанного по экспериментальным данным, с его табличным значением при выбранном заранее уровне значимости a. Уровень значимости a определяет наибольшую вероятность отвергнуть правильную гипотезу, т. е. наибольшую вероятность предположения о том, что экспериментальный результат ошибочен. Например, если уровень значимости выбирают равным 0,05 (что, очень часто делается в технических задачах), то это означает, что допускается 5%-ная вероятность неверного решения и доверительная 95%-ная вероятность верного.
Если найденное по экспериментальным данным значение критерия попадает в область, соответствующую уровню значимости, то проверяемая гипотеза неверна и ее следует отвергнуть, совершив ошибку с вероятностью a. Если же экспериментальное значение критерия попадает в область, соответствующую вероятности (1-a), то проверяемую гипотезу принимают, совершив ошибку, связанную уже с альтернативной гипотезой.
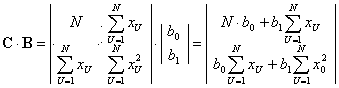
Расчетное значение критерия Кохрена рассчитывается по формуле:
 , (4)
, (4)
где ![]() - наибольшая в ряду дисперсия, которую сравнивают со значением G - критерия, взятым из табл. А1 (приложение А) в зависимости от уровня значимости a, числа степеней свободы fu и числа опытов N: G(a; fu; N). В рассматриваемом случае fu = 2; N = 8.
- наибольшая в ряду дисперсия, которую сравнивают со значением G - критерия, взятым из табл. А1 (приложение А) в зависимости от уровня значимости a, числа степеней свободы fu и числа опытов N: G(a; fu; N). В рассматриваемом случае fu = 2; N = 8.
Из табл. 4 находим максимальную построчную дисперсию ![]() и
и![]() Тогда G pacч = 27,93/78,4 = 0,356.
Тогда G pacч = 27,93/78,4 = 0,356.
Приняв значение уровня значимости a = 0,05, для числа степеней свободы fu = 2 и числа опытов N = 8 получим следующее табличное значение G-критерия: ![]() .
.
Если G pacч < ![]() , ряд дисперсий однороден. Если G pacч >
, ряд дисперсий однороден. Если G pacч > ![]() , ряд дисперсий неоднороден.
, ряд дисперсий неоднороден.
В рассматриваемом примере G pacч > ![]() , т.е. ряд дисперсий неоднороден. Обычно такая ситуация возникает, если среди анализируемых экспериментальных данных имеются грубые ошибки или промахи, связанные с ошибками, допущенными при проведении эксперимента. В таком случае эксперимент следует повторить, тщательно проанализировав его с методологической точки зрения и уделив особое внимание методике сбора и обработки экспериментальных данных. Если при тщательном анализе экспериментальных данных грубых ошибок и промахов не выявлено, неоднородность ряда дисперсий означает, что значения функции отклика (y) действительно определены с разной точностью, однако в каждом отдельном опыте уровень шумов (ошибок) не выходит за границы допустимых значений. Именно такой вывод справедлив для результатов измерений и расчетов, представленных в табл. 4. Во всех дублях значения функции отклика
, т.е. ряд дисперсий неоднороден. Обычно такая ситуация возникает, если среди анализируемых экспериментальных данных имеются грубые ошибки или промахи, связанные с ошибками, допущенными при проведении эксперимента. В таком случае эксперимент следует повторить, тщательно проанализировав его с методологической точки зрения и уделив особое внимание методике сбора и обработки экспериментальных данных. Если при тщательном анализе экспериментальных данных грубых ошибок и промахов не выявлено, неоднородность ряда дисперсий означает, что значения функции отклика (y) действительно определены с разной точностью, однако в каждом отдельном опыте уровень шумов (ошибок) не выходит за границы допустимых значений. Именно такой вывод справедлив для результатов измерений и расчетов, представленных в табл. 4. Во всех дублях значения функции отклика ![]() очень плотно группируются относительно средних значений
очень плотно группируются относительно средних значений ![]() .
.
Похожие работы
вание отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению; планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами; планирование регрессионного эксперимента, позволяющего получать регрессионные модели (полиномиальные и ...
... qвос = 0,05 (в данном случае Gкр=0,3894), то гипотеза об однородности выборочных дисперсий отвечает результатам наблюдений. В данном случае воспроизводимость эксперимента выполняется. 2.4 Построение диаграммы рассеяния Вид диаграммы рассеяния приведен на рисунке 1. Рисунок 1 Рассчитанные значения вкладов и количество выделяющихся точек для соответствующих факторов приведены в ...
... планирование отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению; · планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами; · планирование регрессионного эксперимента, позволяющего получать ...
... ŷ = a0 + a1x , где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии; a0 , a1 - коэффициенты (параметры) уравнения регрессии. Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования ...



0 комментариев