Навигация
Расчет коэффициентов регрессии
4. Расчет коэффициентов регрессии
Модель изучаемого процесса представим в виде обобщенного уравнения:
y = b0 + S(biXi) + S(bijXiXj) + b123X1X2X3. (5)
Применительно к трехфакторному эксперименту уравнение (5) можно записать в виде:
y = b0 + b1X1 + b2X2 + b3X3 + b12X1Х2 + b13X1Х3 + b23X2Х3 + b123X1X2X3, (6)
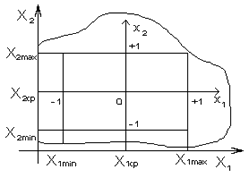
где X1, X2, X3 – кодированные значения уровней факторов (табл. 3). Кодированные значения уровней факторов в уравнении (6) могут принимать значения +1 и -1.
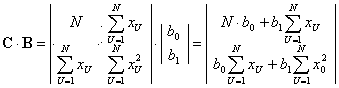
Коэффициенты уравнения регрессии (6) рассчитываются по зависимости:
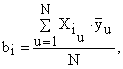 (7)
(7)
где u - номер опыта; ![]() - кодированные значения уровней варьируемых факторов /независимых переменных X1(Al), X2(Mn), X3(С) / (табл. 3);
- кодированные значения уровней варьируемых факторов /независимых переменных X1(Al), X2(Mn), X3(С) / (табл. 3); ![]() - средние арифметические значения функции отклика (интенсивности изнашивания) (табл. 4).
- средние арифметические значения функции отклика (интенсивности изнашивания) (табл. 4).
Распишем уравнение (7) для всех коэффициентов, входящих в регрессионную модель (6):
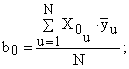
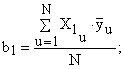
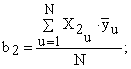
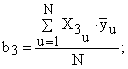 (8)
(8)
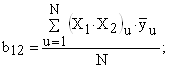
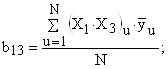
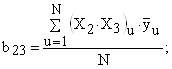

Для расчета коэффициентов регрессии составим расширенную матрицу планирования (табл. 5).
Таблица 5
Расширенная матрица плана 23
| Номер опыта | Х0 | Х1 | Х2 | Х3 | Х4 = Х1 Х2 | Х5 = Х1 Х3 | Х6= Х2 Х3 | Х7 = Х1 Х2 Х3 |
|
| 1 | +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | 97,3 |
| 2 | +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | 127,6 |
| 3 | +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | 153,7 |
| 4 | +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | 71,9 |
| 5 | +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | 113,7 |
| 6 | +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | 91,8 |
| 7 | +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | 127,1 |
| 8 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | 112,2 |
Рассчитаем коэффициенты в уравнении регрессии (6) по зависимостям (8) с учетом знаков Хi в столбцах табл. 5:
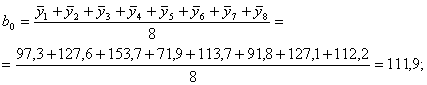
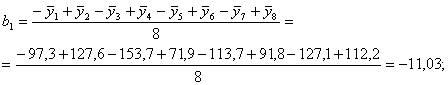
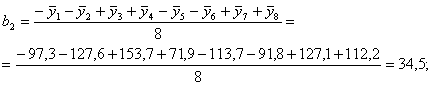
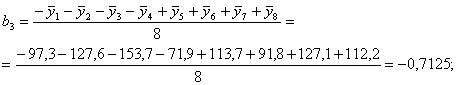
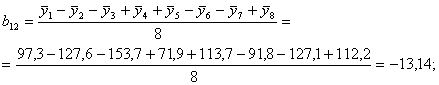



Таким образом, получены следующие значения коэффициентов уравнения регрессии:
b0 = 111,9; b12 = b4 = -13,14;
b1 = -11,03; b13 = b5 = 1,83;
b2 = 34,5; b23 = b6= 4,13;
b3 = -0,7125; b123 = b7 = 14,89.
Если ввести обозначения b12 = b4; b13 = b5; b23 = b6; b123 = b7 и учесть обозначения, принятые в табл. 5, регрессионное уравнение (6) запишется в виде:
y = b0 + b1X1 + b2X2 + b3X3 + b4X4 + b5X5 + b6X6 + b7X7. (9)
Похожие работы
вание отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению; планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами; планирование регрессионного эксперимента, позволяющего получать регрессионные модели (полиномиальные и ...
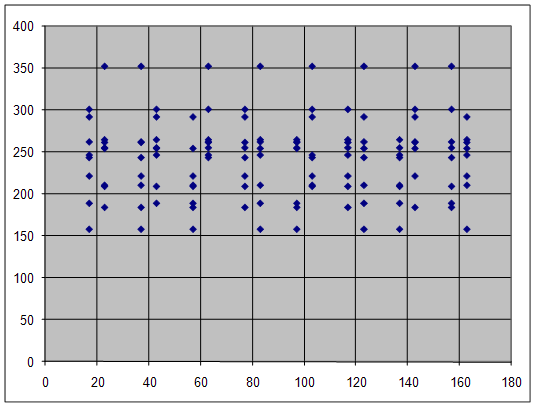
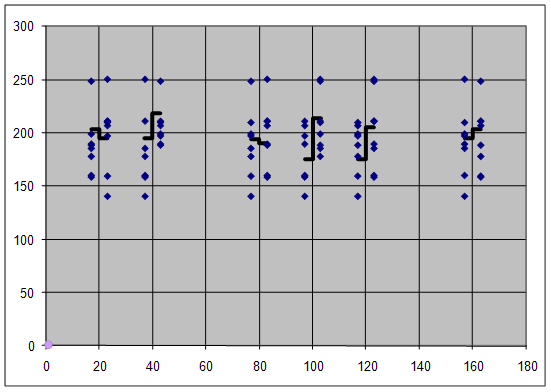
... qвос = 0,05 (в данном случае Gкр=0,3894), то гипотеза об однородности выборочных дисперсий отвечает результатам наблюдений. В данном случае воспроизводимость эксперимента выполняется. 2.4 Построение диаграммы рассеяния Вид диаграммы рассеяния приведен на рисунке 1. Рисунок 1 Рассчитанные значения вкладов и количество выделяющихся точек для соответствующих факторов приведены в ...
... планирование отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению; · планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами; · планирование регрессионного эксперимента, позволяющего получать ...
... ŷ = a0 + a1x , где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии; a0 , a1 - коэффициенты (параметры) уравнения регрессии. Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования ...



0 комментариев