Анализ модели

Исходные данные Расчет дисперсии опыта Расчет коэффициентов регрессии Проверка статистической значимости коэффициентов регрессии Анализ модели

44276

знаков

таблиц

изображение

Проверка статистической значимости коэффициентов регрессии

7. Анализ модели

Все соображения о направлении и силе влияния изученных факторов на износостойкость чугунных тормозных колодок можно высказать только для выбранных интервалов их изменения.

Из анализа полученного уравнения регрессии (15), можно сделать вывод о том, что наиболее существенно увеличивает износостойкость фактор X₃(С), а значит, для изготовления тормозных колодок следует использовать чугун с максимальным содержанием углерода: 3,8 мас. %.

Установлено, что наименьшие удельные потери массы (0,071 г/cм²) получены на образце № 7 (Al - 2,5 %, Mn - 12 %, С - 3,8 %) (табл. 6).

ПРИЛОЖЕНИЕ А

Таблица А1

Критические значения G-критерия (критерия Кохрена) при уровне значимости a = 0,05

Число опытов, N	Число степеней свободы,
Число опытов, N	1	2	3	4	5	6	7	8	9	10	16	36	144
2	0,999	0,975	0,939	0,906	0,858	0,853	0,833	0,816	0,801	0,788	0,734	0,66	0,581
3	0,967	0,871	0,798	0,746	0,707	0,677	0,653	0,633	0,617	0,603	0,547	0,475	0,403
4	0,907	0,768	0,684	0,629	0,59	0,56	0,537	0,518	0,502	0,488	0,437	0,372	0,309
5	0,841	0,684	0,598	0,544	0,506	0,478	0,456	0,439	0,424	0,412	0,365	0,307	0,251
6	0,781	0,616	0,532	0,48	0,445	0,418	0,398	0,382	0,368	0,357	0,314	0,261	0,212
7	0,727	0,561	0,48	0,431	0,391	0,373	0,356	0,338	0,325	0,315	0,276	0,228	0,183
8	0,68	0,516	0,438	0,391	0,36	0,336	0,319	0,304	0,293	0,283	0,246	0,202	0,162
9	0,64	0,478	0,403	0,358	0,329	0,307	0,29	0,277	0,266	0,257	0,223	0,182	0,145
10	0,602	0,445	0,373	0,331	0,303	0,282	0,267	0,254	0,244	0,235	0,203	0,166	0,131
12	0,541	0,392	0,326	0,288	0,262	0,244	0,23	0,219	0,21	0,202	0,174	0,14	0,11
15	0,471	0,335	0,276	0,242	0,22	0,203	0,191	0,182	0,174	0,167	0,143	0,114	0,089
20	0,389	0,271	0,221	0,192	0,174	0,16	0,15	0,142	0,136	0,13	0,111	0,088	0,068
24	0,343	0,235	0,191	0,166	0,149	0,137	0,129	0,121	0,116	0,111	0,094	0,074	0,057
30	0,293	0,198	0,159	0,138	0,124	0,114	0,106	0,1	0,096	0,092	0,077	0,06	0,046
40	0,237	0,158	0,126	0,108	0,097	0,089	0,083	0,078	0,075	0,071	0,06	0,046	0,035
60	0,174	0,113	0,09	0,077	0,068	0,062	0,058	0,055	0,052	0,05	0,041	0,032	0,023
120	0,1	0,063	0,05	0,042	0,037	0,034	0,031	0,029	0,028	0,027	0,022	0,017	0,012

ПРИЛОЖЕНИЕ Б

Таблица Б1

Критические значения t-критерия (критерия Стьюдента)

Число степеней свободы,	Уровень значимости, a			Число степеней свободы,	Уровень значимости, a
Число степеней свободы,	0,1	0,05	0,01	Число степеней свободы,	0,1	0,05	0,01
1	6,31	12,7	63,66	16	1,75	2,12	2,92
2	2,92	4,3	9,93	17	1,74	2,11	2,9
3	2,35	3,18	5,84	18	1,73	2,1	2,88
4	2,13	2,78	4,6	19	1,73	2,09	2,86
5	2,02	2,57	4,03	20	1,73	2,08	2,85
6	1,94	2,45	3,71	21	1,72	2,08	2,83
7	1,9	2,37	3,5	22	1,72	2,07	2,82
8	1,86	2,31	3,36	23	1,71	2,07	2,81
9	1,83	2,26	3,25	24	1,71	2,06	2,8
10	1,81	2,23	3,17	25	1,71	2,06	2,79
11	1,8	2,2	3,11	26	1,71	2,06	2,78
12	1,78	2,18	3,06	27	1,7	2,05	2,77
13	1,77	2,16	3,01	28	1,7	2,05	2,76
14	1,76	2,15	2,98	29	1,7	2,04	2,75
15	1,75	2,13	2,95	30	1,7	2,04	2,75

ПРИЛОЖЕНИЕ В

Таблица В1

Значения критерия Фишера (F-критерия) при уровне значимости a = 0,05

Число степеней свободы,	Число степеней свободы, (N – количество опытов; - количество статистически значимых коэффициентов в регрессионном уравнении)
Число степеней свободы,	1	2	3	4	5	6	7	8	9	10	12	14	16	20	24	30
2	18,51	19	19,16	19,25	19,3	19,33	19,36	19,37	19,38	19,39	19,41	19,42	19,43	19,44	19,45	19,46
3	10,13	9,55	9,28	9,12	9,01	8,94	8,88	8,84	8,81	8,78	8,74	8,71	8,69	8,66	8,64	8,62
4	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04	6	5,96	5,91	5,87	5,84	5,8	5,77	5,74
5	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82	4,78	4,74	4,68	4,64	4,6	4,56	4,53	4,5
6	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15	4,1	4,06	4	3,96	3,92	3,87	3,84	3,81
7	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73	3,68	3,63	3,57	3,52	3,49	3,44	3,41	3,38
8	5,32	4,46	4,07	3,84	3,69	3,58	3,5	3,44	3,39	3,34	3,28	3,23	3,2	3,15	3,12	3,08
9	5,12	4,26	3,86	3,63	3,48	3,37	3,29	3,23	3,18	3,13	3,07	3,02	2,98	2,93	2,9	2,86
10	4,96	4,1	3,71	3,48	3,33	3,22	3,14	3,07	3,02	2,97	2,91	2,86	2,82	2,77	2,74	2,7
11	4,84	3,98	3,59	3,36	3,2	3,09	3,01	2,95	2,9	2,86	2,79	2,74	2,7	2,65	2,61	2,57
12	4,75	3,88	3,49	3,26	3,11	3	2,92	2,85	2,8	2,76	2,69	2,64	2,6	2,54	2,5	2,46
13	4,67	3,8	3,41	3,18	3,02	2,92	2,84	2,77	2,72	2,67	2,6	2,55	2,51	2,46	2,42	2,38
14	4,6	3,74	3,34	3,11	2,96	2,85	2,77	2,7	2,65	2,6	2,53	2,48	2,44	2,39	2,35	2,31
15	4,54	3,68	3,29	3,06	2,9	2,79	2,7	2,64	2,59	2,55	2,48	2,43	2,39	2,33	2,29	2,25
16	4,49	3,63	3,24	3,01	2,85	2,74	2,66	2,59	2,54	2,49	2,42	2,37	2,33	2,28	2,24	2,2
17	4,45	3,59	3,2	2,96	2,81	2,7	2,62	2,55	2,5	2,45	2,38	2,33	2,29	2,23	2,19	2,15
18	4,41	3,55	3,16	2,93	2,77	2,66	2,58	2,51	2,46	2,41	2,34	2,29	2,25	2,19	2,15	2,11
19	4,38	3,52	3,13	2,9	2,74	2,63	2,55	2,48	2,43	2,38	2,31	2,26	2,21	2,15	2,11	2,07
20	4,35	3,49	3,1	2,87	2,71	2,6	2,52	2,45	2,4	2,35	2,28	2,23	2,18	2,12	2,08	2,04
21	4,32	3,47	3,07	2,84	2,68	2,57	2,49	2,42	2,37	2,32	2,25	2,2	2,15	2,09	2,05	2
22	4,3	3,44	3,05	2,82	2,66	2,55	2,47	2,4	2,35	2,3	2,23	2,18	2,13	2,07	2,03	1,98
23	4,28	3,42	3,03	2,8	2,64	2,53	2,45	2,38	2,32	2,28	2,2	2,14	2,1	2,05	2	1,96
24	4,26	3,4	3,01	2,78	2,62	2,51	2,43	2,36	2,3	2,26	2,18	2,13	2,09	2,02	1,98	1,94

Число степеней свободы,	Число степеней свободы, (N – количество опытов; - количество статистически значимых коэффициентов в регрессионном уравнении)
Число степеней свободы,	1	2	3	4	5	6	7	8	9	10	12	14	16	20	24	30
25	4,24	3,38	2,99	2,76	2,6	2,49	2,41	2,34	2,28	2,24	2,16	2,11	2,06	2	1,96	1,92
26	4,22	3,37	2,98	2,74	2,59	2,47	2,39	2,32	2,27	2,22	2,15	2,1	2,05	1,99	1,95	1,9
27	4,21	3,35	2,96	2,73	2,57	2,46	2,37	2,3	2,25	2,2	2,13	2,08	2,03	1,97	1,93	1,88
28	4,2	3,34	2,95	2,71	2,56	2,44	2,36	2,29	2,24	2,19	2,12	2,06	2,02	1,96	1,91	1,87
29	4,18	3,33	2,93	2,7	2,54	2,43	2,35	2,28	2,22	2,18	2,1	2,05	2	1,94	1,9	1,85
30	4,17	3,32	2,92	2,69	2,53	2,42	2,34	2,27	2,21	2,16	2,04	2	1,99	1,93	1,89	1,84
32	4,15	3,3	2,9	2,67	2,51	2,4	2,32	2,25	2,19	2,14	2,07	2,02	1,97	1,91	1,86	1,82
34	4,13	3,28	2,88	2,65	2,49	2,38	2,3	2,23	2,17	2,12	2,05	2	1,95	1,89	1,84	1,8
36	4,11	3,26	2,86	2,63	2,48	2,36	2,28	2,21	2,15	2,1	2,03	1,98	1,93	1,87	1,82	1,78
38	4,1	3,25	2,85	2,62	2,46	2,35	2,26	2,19	2,14	2,09	2,02	1,96	1,92	1,85	1,8	1,76
40	4,08	3,23	2,84	2,61	2,45	2,34	2,25	2,18	2,12	2,07	2	1,95	1,9	1,84	1,79	1,74
42	4,07	3,22	2,83	2,59	2,44	2,32	2,24	2,17	2,11	2,06	1,99	1,94	1,89	1,82	1,78	1,73
44	4,06	3,21	2,82	2,58	2,43	2,31	2,23	2,16	2,1	2,05	1,98	1,92	1,88	1,81	1,76	1,72
46	4,05	3,2	2,81	2,57	2,42	2,3	2,22	2,14	2,09	2,04	1,97	1,91	1,87	1,8	1,75	1,71
48	4,04	3,19	2,8	2,56	2,41	2,3	2,21	2,14	2,08	2,03	1,96	1,9	1,86	1,79	1,74	1,7
50	4,03	3,18	2,79	2,56	2,4	2,29	2,2	2,13	2,07	2,02	1,95	1,9	1,85	1,78	1,74	1,69
55	4,02	3,17	2,78	2,54	2,38	2,27	2,18	2,11	2,05	2	1,93	1,88	1,83	1,76	1,72	1,67
60	4	3,15	2,76	2,52	2,37	2,25	2,17	2,1	2,04	1,99	1,92	1,86	1,81	1,75	1,7	1,65
65	3,99	3,14	2,75	2,51	2,36	2,24	2,15	2,08	2,02	1,98	1,9	1,85	1,8	1,73	1,68	1,63
70	3,98	3,13	2,74	2,5	2,35	2,23	2,14	2,07	2,01	1,97	1,89	1,84	1,79	1,72	1,67	1,62
80	3,96	3,11	2,72	2,48	2,33	2,21	2,12	2,05	1,99	1,95	1,88	1,82	1,77	1,7	1,65	1,6
100	3,94	3,09	2,7	2,46	2,3	2,19	2,1	2,03	1,97	1,92	1,85	1,79	1,75	1,68	1,63	1,57
125	3,92	3,07	2,68	2,44	2,29	2,17	2,08	2,01	1,95	1,9	1,83	1,77	1,72	1,65	1,6	1,55
150	3,91	3,06	2,67	2,43	2,17	2,16	2,07	2	1,94	1,89	1,82	1,76	1,71	1,64	1,59	1,54
200	3,89	3,04	2,65	2,41	2,26	2,14	2,05	1,98	1,92	1,87	1,8	1,74	1,69	1,62	1,57	1,52
400	3,86	3,02	2,62	2,39	2,23	2,12	2,03	1,96	1,9	1,85	1,78	1,72	1,67	1,6	1,54	1,49

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Статистические методы обработки эмпирических данных / В.А. Грешников, Б.Н. Волков, А.И. Кубарев - М.: Изд-во стандартов. – 1978. - 232с.

2. Барабашук В.И. Планирование эксперимента в технике. - К.: Техніка. – 1984. - 200с.

3. Эрнесто Рафалес-Ламарка. Методология научно-технического исследования. – Луганск. – 1992. – 218с.

4. Волченко В.Н. Статистические методы управления качеством по результатам неразрушающего контроля. – М.: Машиностроение. – 1976. – 64с.

5. Ноулер Л., Хауэлл Дж., Голд Б. Статистические методы контроля качества продукции. – М.: Изд-во стандартов. – 1984. – 104с.

6. Новик Ф.С., Арсов Я.Б. Оптимизация процессов технологии металлов методами планирования экспериментов. – М.: Машиностроение. – 1980. – 304с.

7. Розанов Ю.Н. Методы математической статистики в материаловедении. – Л.: Машиностроение. – 1990. – 232с.

8. Дьяконов В.П., Абраменкова И.В. MathCAD в математике, физике и в Internet. – М.: Нолидж, 1999. – 352с.

Проверка статистической значимости коэффициентов регрессии

Раздел: Экономико-математическое моделирование
Количество знаков с пробелами: 44276
Количество таблиц: 10
Количество изображений: 1

Скачать

вание отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению; планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами; планирование регрессионного эксперимента, позволяющего получать регрессионные модели (полиномиальные и ...

Скачать

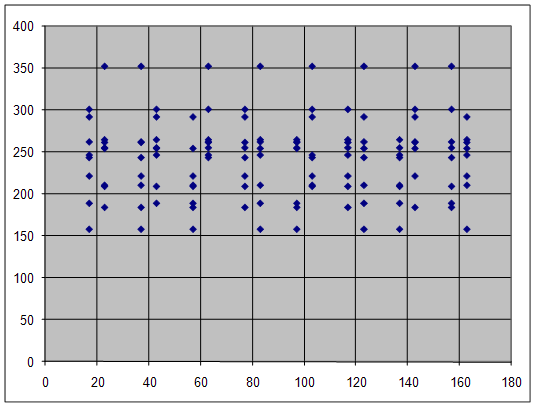
... qвос = 0,05 (в данном случае Gкр=0,3894), то гипотеза об однородности выборочных дисперсий отвечает результатам наблюдений. В данном случае воспроизводимость эксперимента выполняется. 2.4 Построение диаграммы рассеяния Вид диаграммы рассеяния приведен на рисунке 1. Рисунок 1 Рассчитанные значения вкладов и количество выделяющихся точек для соответствующих факторов приведены в ...

Скачать

... планирование отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению; · планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами; · планирование регрессионного эксперимента, позволяющего получать ...

Скачать

... ŷ = a0 + a1x , где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии; a0 , a1 - коэффициенты (параметры) уравнения регрессии. Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

0 комментариев

Разделы

Инфо

Следите за новостями