Расчет квантово-химических параметров ФАВ и определение зависимости "структура-активность" на примере сульфаниламидов

 

РАСЧЕТ КВАНТОВО – ХИМИЧЕСКИХ ПАРАМЕТРОВ ФАВ И ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ «СТРУКТУРА – АКТИВНОСТЬ» НА ПРИМЕРЕ СУЛЬФАНИЛАМИДОВ

ОГЛАВЛЕНИЕ

ПЕРЕЧЕНЬ СОКРАЩЕНИЙ

ВВЕДЕНИЕ

Глава 1. МАТЕМАТИЧЕСКИЕ МЕТОДЫ РАСЧЕТА КОНСТАНТ ОРГАНИЧЕСКИХ МОЛЕКУЛ И ВИДОВ ПРОЯВЛЯЕМОЙ ФИЗИОЛОГИЧЕСКОЙ АКТИВНОСТИ

1.1 История развития квантовохимических методов анализа «структура вещества – проявляемая физиологическая активность»

1.1.1 Различие неэмпирических и полуэмпирических методов

1.1.2 Метод Хартри - Фока

1.1.3 Метод Хэнча

1.1.4 Регрессионный анализ и статистические параметры

1.1.5 Аддитивная модель Фри – Вильсона

1.1.6 Метод Хюккеля, расширенный метод Хюккеля

1.2 Современные методы анализа «структура вещества – проявляемая физиологическая активность»

1.2.1 Принципы распознавания образов

1.2.2 Основные понятия методов распознавания образов

1.2.3 Методы кластеризации

1.2.4 Программа PASS C&T

1.3 Вывод

Глава 2. ВЫЧИСЛЕНИЕ ГЕОМЕТРИИ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ

2.1 Квантовохимические методы расчета

2.1.1 Расчет потенциалов ионизации

2.1.2 Расчет индексов реакционной способности

2.1.3 Вычисление теплот образования

2.1.4 Расчет тепловых эффектов органических реакций

2.1.5 Расчет поверхностей потенциальной энергии

2.1.6 Силовые постоянные химических связей и частоты внутримолекулярных колебаний

2.2 Вывод

Глава 3. СУЛЬФАНИЛАМИДНЫЕ ЛЕКАРСТВЕННЫЕ ПРЕПАРАТЫ

3.1 История открытия сульфаниламидов

3.2 Физические свойства сульфаниламидов

3.3 Механизм действия сульфаниламидов

3.4 Синтез сульфаниламидов

3.5 Расчитанные параметры молекул

3.5.1 Сульфаниламид

3.5.2 Сульгин

3.5.3 Сульфадимезин

3.5.4 Норсульфазол

3.5.4 Сульфафуразол

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

Приложение А

Приложение Б

Приложение В

Приложение Г

Приложение Д

Приложение Е

Приложение Ж

ПЕРЕЧЕНЬ СОКРАЩЕНИЙ

В данной дипломной работе применены следующие сокращения:

АО - атомная орбиталь

МО - молекулярная орбиталь

ЛКАО - линейная комбинация атомных орбиталей

МО ЛКАО - молекулярные орбитали, представленные в виде линейных комбинаций атомных орбиталей

ССП - самосогласованное поле

ППЭ - поверхность потенциальной энергии

ППДП - полное пренебрежение дифференциальным перекрыванием (в зарубежной литературе CNDO)

ЧПДП - частичное пренебрежение дифференциальным перекрыванием (в зарубежной литературе INDO)

ПДДП - пренебрежение двухатомным дифференциальным перекрыванием (в зарубежной литературе NDDO)

ППДП/2 - полуэмперический метод, предложенный Пополом, Сантри и Сергалом, в котором использовано приближение ППДП, второй вариант

ЧПДП - аналогичный метод, в котором использовано приближение ППДП

ППДП/БУ - полуэмпирический метод, предложенный Бойдом и Уайтхедом, в котором использовано приближение ППДП

МПДП - полуэмпирический метод разработанный, Дьюаром и сотрудниками, в котором использовано приближение ПДДП

МПДП/Н - модифицированный вариант метода МПДП для расчетов параметров систем с водородными связями

АМ1 - новый вариант метода МПДП, разработанный Дьюаром с сотрудниками

ССП - самосогласованное поле

КВ – метод конфигурационного взаимодействия учета электронной корреляции

ПАБК – пара – аминобензойная кислота

ЖКХ – желудочно–кишечный тракт

PASS C&T - Prediction of Activity Spectra for Substances: Complex & Training

ВВЕДЕНИЕ

С давних лет человечество мечтает о лекарстве, которое при действии на организм обладало бы максимальной избирательностью, благодаря чему эффективно устраняется причина болезни, но не возникают нежелательные побочные эффекты. Наиболее ярко эта идея выражена в концепции "магической пули", выдвинутой основателем химиотерапии П. Эрлихом.

В то же время, весь накопленный к настоящему моменту опыт медицинской химии и фармакологии свидетельствует об отсутствии абсолютной специфичности действия известных лекарственных веществ: все они способны вызывать многообразные фармакологические эффекты, часть которых используется для терапии определенной патологии, а другие - являются причиной побочного действия и токсичности. Полный набор фармакологических эффектов, которые может проявить некое вещество в различных условиях эксперимента, называется спектром биологической активности данного вещества.

В процессе исследования нового фармакологического вещества характеристики спектра его биологической активности выявляются не сразу: некоторые эффекты обнаруживаются уже при первом тестировании "в пробирке", другие - при изучении его действия на экспериментальных животных, третьи - при проведении клинических испытаний и последующем использовании препарата в медицинской практике. Нередко новое действие выявляется у вещества, применяемого в медицине в течение многих лет. Такое открытие может стать основой для использования препарата по новому назначению. Например:

1. вальпроат был первоначально предложен в качестве анксиолитика в 1961 г. и как противоэпилептическое средство - в 1989 г.;

2. левамизол - как антигельминтное средство в 1968 г. и как иммуностимулятор - в 1980 г.;

3. альпростадил - как антиагрегантное средство в 1988 г. и как препарат, стимулирующий эрекцию - в 1994 г.;

4. аспирин был предложен в качестве анальгетика в 1899 г., а его антиагрегантное действие было открыто лишь в 1971 г.; и т.д. [1].

5. талидомид, обладающий анксиолитическим и снотворным эффектами, был введен в медицинскую практику в 50-х годах [2]. В начале 60-х годов из-за наличия тератогенности он стал причиной врожденных дефектов у более чем 8000 новорожденных в Европе [3], что привело к запрету на его применение и ужесточению требований к исследованию безопасности лекарственных препаратов вообще. Теперь, сорок лет спустя, талидомид переживает "второе рождение". Он активно испытывается в клинике как потенциальное противоопухолевое и антиметастатическое средство, как препарат для симптоматической терапии СПИДа. Это обусловлено его недавно открытыми антиангиогенным эффектом [4] и антагонистическим действием по отношению к фактору некроза опухоли [5]. В сентябре 1997 года Администрация по лекарствам и пищевым продуктам США даже устроила специальное открытое совещание, посвященное современным оценкам соотношения "польза - риск" при использовании талидомида в медицинской практике.

Если бы можно было предсказать вероятность проявления веществом конкретных видов биологической активности заранее, то его дорогостоящее исследование в эксперименте и клинике проводилось бы более прицельно, и позволило бы выявить многие полезные и побочные эффекты на ранних стадиях изучения препарата.

Основа для такого предсказания известна достаточно давно, и она связана с утверждением: "Биологическая активность вещества является функцией его химической структуры ". Надо "всего лишь" выявить вид этой функции и в дальнейшем "подставить в уравнение" структурную формулу исследуемого вещества, получив в результате прогностическую оценку его биологической активности. В сущности, именно так и поступают в медицинской химии: анализируя химическое строение соединений с известной биологической активностью, выделяют элементы, "ответственные" за проявление/отсутствие того или иного эффектов, и далее "конструируют" молекулы более активных и менее токсичных аналогов. [6]

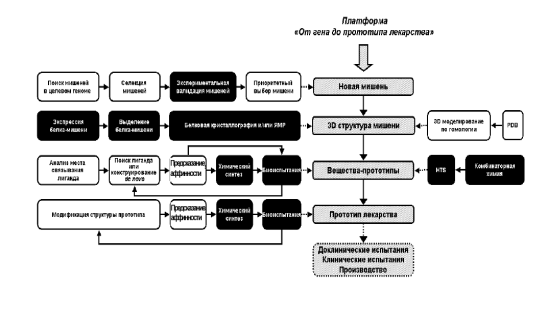
Рисунок 1.1 Общая структура платформы от гена до прототипа лекарства. Экспериментальные блоки показаны черным цветом, компьютерные – белым.

Это положение послужило основанием для выделения у химических соединений определенных факторов (дескрипторов) и установления связи, качественной (SAR) или количественной (QSAR), между ними и биологической активностью соединения. В качестве таких дескрипторов используются различные характеристики молекулы:

1. топологические – фрагменты структуры (подструктурные дескрипторы), индексы атомов и связей, каппа - индексы, описывающие форму молекулы, индексы молекулярных связей (MCI);

2. квантовые параметры – энергии HOMO (высшей занятой обитали) и LUMO (низшей незанятой обитали), заряды на различных атомах, электронные плотности, поляризуемости;

3. параметры, относящиеся к целой молекуле – молярная рефракция, коэффициент распределения октанол - вода.

В данной работе будет рассмотрена возможность проведения анализа «структура вещества – проявляемая физиологическая активность» на примере соединений сульфаниламидного ряда. Сульфаниламиды относятся к лекарственным веществам противостафилакоккового направления бактериостатического принципа действия. Так же они проявляют антидиабетические, диуретические и антисептические свойства. Более подробно сульфаниламиды рассмотрены в главе 3.

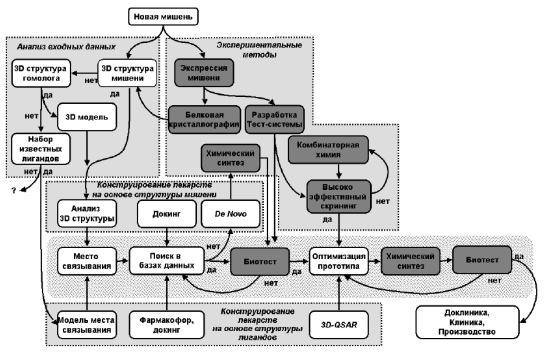
Рисунок 1.2 Общая схема стратегии компьютерного конструирования лекарств.

Квантовая механика и статистическая физика в принципе позволяют дать исчерпывающее объяснение любым экспериментальным данным о реакционной способности органических соединений и предсказать возможные направления реакций, а так же виды проявляемой физиологической активности.

В данной работе будет рассмотрена возможность не только расчета параметров соединения, что позволит химикам – синтетикам еще до получения конкретного соединения предсказать его физико – химические свойства, но и будет предложен метод для расчета физиологической активности соединения. Ни в зарубежной, ни в отечественной литературе эти методы ранее в совокупности не рассматривались, и возможности перехода от одного к другому не исследовались.

Глава 1 МАТЕМАТИЧЕСКИЕ МЕТОДЫ РАСЧЕТА КОНСТАНТ ОРГАНИЧЕСКИХ МОЛЕКУЛ И ВИДОВ ПРОЯВЛЯЕМОЙ ФИЗИОЛОГИЧЕСКОЙ АКТИВНОСТИ

  1.1 История развития квантовохимических методов анализа «структура вещества – проявляемая физиологическая активность»

В основе квантовой механики лежит уравнение Шредингера, играющее в ней такую же важную роль, как и уравнения Ньютона в классической механике. Также как и уравнения Ньютона, уравнение Шредингера не выведено ни из какой физической теории, а является постулатом, полученным в результате обобщения опытных фактов.

Для совокупности N взаимодействующих частиц с потенциальной энергией U и массами mk в декартовой системе координат оно имеет вид

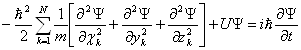
где Ψ(x, y, z, t) – волновая функция совокупности координат системы частиц и времени, U – оператор потенциальной энергии. Суммирование производится по всем частицам.

Стационарные состояния удовлетворяют не зависящему от времени уравнению Шредингера:

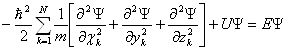
Параметр Е есть собственное значение стационарного уравнения Шредингера. В результате решения стационарного уравнения Шредингера находят собственные (возможные) значения параметра Е и соответствующие ему решения – собственные функции.

Для любого уравнения Шредингера, соответствующего конкретной системе, существует бесконечное множество значений параметра Е. Эти значения могут быть как непрерывными (для свободно движущейся частицы), так и дискретными, если частицы локализованы в малой области пространства. Дискретные значения Е называют уровнями энергии.

Пользуясь операторной символикой, можно записать уравнение Шредингера в сокращенной форме:

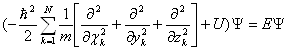
ĤΨ = ЕΨ,

где Ĥ = 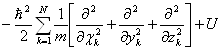- оператор Гамильтона или гамильтониан системы частиц.

1970 - 1980-е годы были временем очень быстрого развития вычислительных методов квантовой химии. В результате появилась возможность рассчитывать геометрию и оценивать стабильность промежуточных продуктов и переходных состояний, а также вычислять профили поверхности потенциальной энергии вдоль координаты реакции. Экспериментальное получение подобной информации для большинства реакций связано с преодолением значительных трудностей, вызванных многостадийным характером процессов, синхронным протеканием отдельных элементарных стадий и очень малым временем жизни промежуточных продуктов. Развитие вычислительных методов квантовой химии и появление быстродействующих ЭВМ позволили рассчитывать многие характеристики органических соединений, в том числе и нестабильных, а также переходных состояний. Точность этих расчетов получается вполне удовлетворительной по термохимическим стандартам. Поэтому квантовохимические расчеты в настоящее время используются в качестве одного из физико-химических методов исследования для получения данных, необходимых для установления механизмов сложных органических реакций.

Существующие методы математического моделирования "структура- активность" могут быть условно разделены на три группы.

Первая группа основана на использовании принципа линейности свободных энергий и включает в себя такие подходы, как метод Хэнча, метод Кубиньи и "диффузионный подход".

К этой же группе причисляют аддитивно- статистические методы Фри - Уилсона, Фуйита - Бана, Каммарата - Яу и им подобные. Для построения моделей, реализующих принцип линейности свободных энергий, используются методы регрессионного анализа.

Вторая группа объединяет методы, предназначенные для получения первоначальных представлений об изучаемом явлении посредством статистической обработки всей имеющейся информации, а также преобразования ее к виду, удобному для дальнейшего использования. Эта группа методов иногда называется методами "генерации гипотез". Она объединяет такие методы, как факторный анализ во всех его модификациях, методы линейного отображения, иногда к этой группе относят и аддитивно- статистические методы.

В третью группу включают методы, основанные на использовании алгоритмов теории распознавания образов, предназначенные для классификации объектов посредством разнообразных статистических и эвристических процедур. К этой группе относят различные методы дискриминантного анализа, порогового логического элемента и его модификации, методы теории алгебры логики.