Верхні напівґрати

1. Верхні напівґрати

Визначення: множина називається верхніми напівґратами, якщо sup{a,b} існує для будь-яких елементів a і b.

Визначення: Непуста множина I верхніх напівґрат L називається ідеалом, якщо для будь-яких  включення  має місце тоді й тільки тоді, коли .

Визначення: Верхні напівґрати  називаються дистрибутивної, якщо нерівність ≤   ( , ,  L) спричиняє існування елементів , таких, що , , і  = .(мал.1). Помітимо, що елементи  й  не обов'язково єдині.

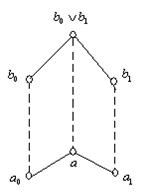
Деякі найпростіші властивості дистрибутивних верхніх напівґрат дає:

Лема 1:

(*). Якщо < , > - довільні напівґрати, то верхні напівґрати  дистрибутивна тоді й тільки тоді, коли ґрати  дистрибутивна.

(**). Якщо верхні напівґрати  дистрибутивна, то для будь-яких  існує елемент , такий, що  й . Отже, множина  є ґратами.

(***). Верхні напівґрати  дистрибутивна тоді й тільки тоді, коли множина  є дистрибутивними ґратами.

Доказ.

(*).  < , > - дистрибутивна й , те для елементів , , справедлива рівність :

виходить, напівґрати < , > - дистрибутивна.

< , > - дистрибутивна. Нехай ґрати  містять діамант або пентагон (мал.2).

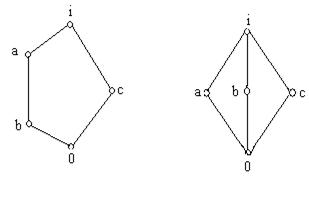
1) Нехай ґрати  містять пентагон, . Потрібно знайти такі елементи  й , щоб виконувалася рівність . Але множина елементів менших b або c складається з елементів {0,b,c} і їхня нижня границя не дасть a. Одержали протиріччя з тим, що < , > - дистрибутивна. Виходить, наше припущення невірно й ґрати  не містять пентагона.

2) Нехай ґрати  містять діамант, . Аналогічно, множина елементів менших b або c складається з елементів {0,b,c}, їхня нижня границя не дасть a. Виходить, ґрати  не містять діаманта.

Можна зробити висновок, що ґрати  дистрибутивна.

(**). Маємо , тому , де (по визначенню дистрибутивних напівґрат). Крім того,  є нижньою границею елементів  і .

Розглянемо ідеали, що містять елемент  і  -  і . Тоді  Ø ,тому що , нижня границя елементів a і b, утримується там.

Покажемо, що I(L) – ґрати, тобто існують точні нижня й верхня грані для будь-яких A і B.

Покажемо, що  збігається з перетинанням ідеалів A і B. По-перше,  - ідеал. Дійсно,  і  й  По-друге, нехай ідеал  і . Тоді , тобто  - точна нижня грань ідеалів A і B, тобто .

Тепер покажемо, що  збігається з перетинанням всіх ідеалів , що містять A і B. Позначимо . Оскільки  для   для  , те C ідеал. По визначенню C він буде найменшим ідеалом, що містить A і B.

(***).  Нехай  – верхні дистрибутивні напівґрати. Покажемо, що

.

Нехай , тобто  (мал.3), для деяких  

Зрозуміло, що . По дистрибутивності, існують  такі, що . Т.к. A – ідеал, те, тому що . Аналогічно, . Т.е. . Точно також, . Якщо , то легко показати, що .

Довели, що  - ідеал. Очевидно, він є верхньою гранню ідеалів A і B. Якщо C містить A і B, то C буде містити елементи  для будь-яких , тобто  Тому , оскільки  є верхньою гранню ідеалів A і B і втримується в будь-який верхній грані.

Тепер покажемо, що виконується рівність:

.

. Нехай , де , .  , те, звідки  й отже . Аналогічно, , виходить,

. Нехай ,де    .

Звідси треба дистрибутивність ґрати .

  – дистрибутивні ґрати, . Тепер розглянемо ідеали, утворені цими елементами:

( ,буде нижньою границею для ). Тому , що й доводить дистрибутивність напівґрат . :

Похожие работы

Прогностичні дослідження маїбутнього

Скачать

75328

1

4

... ЄТЬСЯ, що Одкровення було записано близько 66 року н.е. і, імовірно, доповнене Іоанном згодом через 30 років. З тих пір не проходило жодного століття (а в наш час і жодного року) без нових досліджень і тлумачень цього пророцтва. Число разючих збігів із пророкуванням Іоанна в кожнім столітті було велике, іноді навіть доходило до критичної маси, коли віруючі тієї чи інша країни готувалися до "кінця ...

Проектування екологічних мереж Ратнівського району

Скачать

192341

49

14

... видів риб та водоплавних та навколоводних птахів. З птахів домінують гусеподібні, сивкоподібні, а також зустрічаються норцеподібні, лелекоподібні, журавлеподібні і горобцеподібні. Розділ 4. Проектування екологічних мереж Ратнівського району 4.1 Загальні поняття Сучасна стратегія охорони природи полягає у забезпеченні динамічної екологічної рівноваги окремих регіонів, пошуку різноманітних ...