Навигация
Оценка ожидаемой точности полученных результатов
1.5 Оценка ожидаемой точности полученных результатов
Я определила среднюю квадратическую ошибку положения точки для каждого варианта засечки по формуле:
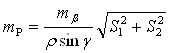 (3)
(3)
где mβ – средняя квадратическая ошибка измерения углов (в задании принимаем mβ=10''),
![]() - угол в треугольнике при точке Р,
- угол в треугольнике при точке Р,
S1, S2 – стороны засечки, м (определены по схеме),
![]() =206265''.
=206265''.
Среднюю квадратическую ошибку координат, полученных из двух вариантов засечки, нашла из формулы:
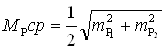 (4).
(4).
углы γ нашла по определению, что сумма углов треугольника равна 180°: для АВР γ=180°-(88°56'20''+43°04'20'')=47°59'20''
для СВР γ=180°-(29°53'08''+91°03'39'')=59°03'13''
![]()
![]()
Из формулы (4) нащла среднюю квадратическую ошибку координат, полученных из двух вариантов засечки:
![]() м
м
Итак, в этой задаче я решила два варианта прямой многократной засечки и вычислила координаты дополнительного пункта. Расхождения координат, полученных в первом и втором вариантах засечки оказались в допуске, поэтому за окончательное значение координат исходного пункта Р я приняла Х=5310,455 и Y=3040,655. При оценке точности полученных результатов получила следующие ошибки:
- среднюю квадратическую ошибку положения торчки Р для каждого варианта засечки: mp1=0,079 м, mp2=0,064 м
- среднюю квадратическую ошибку координат, полученных из двух вариантов засечки: MpCp=0,051 м
2. Вычисление координат дополнительного пункта, определенного обратной многократной засечкой
2.1 Общие указания и исходные данные
Обратная засечка – это задача по определению четвертого пункта по трем данным пунктам и двум измеренным при определяемом пункте углам.
Для контроля правильности решения задачи при определяемой точке измеряют третий угол между направлениями на один из первых трех пунктов и на четвертый данный пункт.
Таким образом, для решения задачи с контролем необходимо видеть из определяемой точки четыре пункта исходной сети и измерить при определяемой точке три угла.
При решении задачи я воспользовалась исходными данными, исправленными с учетом порядкового номера, которые приведены в таблице 3.
Таблица 3 – Исходные данные для решения обратной засечки.
| название пункта | координаты | измеренные на пункте Р направления | |
| X | Y | ||
| 1 | 7105,31 | 3851,55 | 0 |
| 2 | 6613,86 | 3816,43 | 59 |
| 3 | 6653,66 | 2959,70 | 177 |
| 4 | 7353,17 | 3210,20 | 273 |
Порядок решения задачи:
1. составление схемы расположения определяемого и исходных пунктов
2. выбор наилучших вариантов засечки
3. решение наилучших вариантов засечки
4. оценка ожидаемой точности полученных результатов.
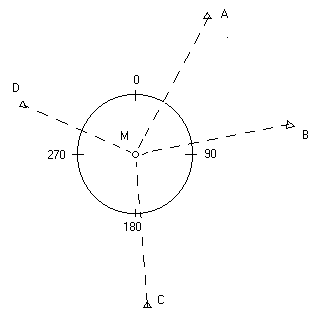
2.2 Составление схемы расположения определяемого и исходного пунктов
Составление схемы я произвела на листе миллиметровой бумаги формата А4. При этом оцифровала её в масштабе 1:10000. По координатам из таблицы 3 нанесла исходные пункты А, В, C, D (приложение Б). Искомый пункт Р нанесла по направлениям (по способу Болотова) на листе кальки формата А4 (приложение В).
Похожие работы
... 1 5008,50 1000,00 1753,45 2748,03 2376,28 72 º28'50'' 101 º12'25'' 351 º18'32'' Луговое Аграрное Свобода 2. Уравновешивание систем ходов плановой съемочной сети 2.1 Уравновешивание систем теодолитных ходов с одной узловой точкой 2.1.1 Задание Произвести уравновешивание систем теодолитных ходов, сходящихся в узловой точке 3 и опирающихся ...
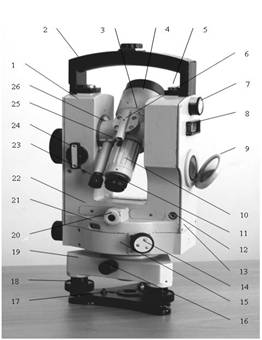
... с ценой деления 1 сек. Области применения: построение геодезических сетей сгущения (триангуляция 4 класса, полигонометрия IV класса), в прикладной геодезии (строительство, изыскания и т.д.), астрономо- геодезических измерениях (определение азимута по Солнцу и по Полярной Звезде). Модель 3Т5КП предназначена для измерения горизонтальных и вертикальных углов и не имеет микрометра. Области ...
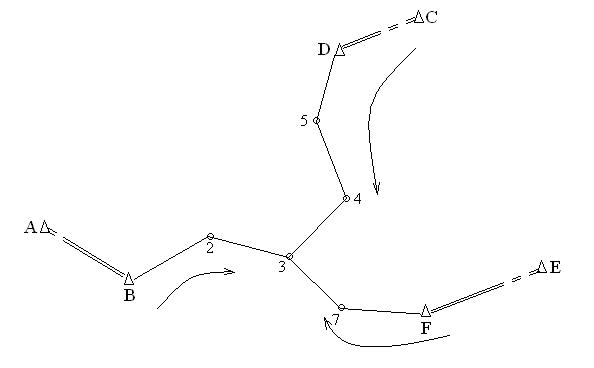
... по формуле: ¦x=åDx-(xк-xн); ¦y=åDy-(yк-yн) сумма поправок приращений должна равнятся нулю. dxBC+dxCD+dXDE+¦x=0 dyBC+dyCD+dyDE+¦=0 4. Упрощенное уравнивание центральной системы. В центральной системе возникает условное уравнение фигур, горизонта и полюса. Математически эти условия выражаются уравнениями поправок. Число условных уравнений фигур ...
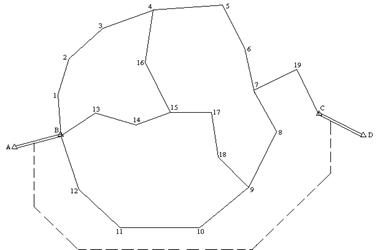
... в полосе съемке со смежных станций. В простейшем случае составление плана по результатам тахеометрической съемки начинают с построения координатной сетки и нанесению по координатам точек теодолитного хода. Правильность нанесения точек хода контролируют по длинам его сторон: измеряют расстояния между вершинами – выраженными в масштабе, они должны быть равны расстояниям между соответствующими ...




0 комментариев