Выбор наилучших вариантов засечки
Оценка ожидаемой точности полученных результатов
Выбор наилучших вариантов засечки
Оценка ожидаемой точности результатов
Вычисление и уравнивание дирекционного угла узловой стороны
Вычисление и уравнивание координат узловой точки
Уравнивание ходов технического нивелирования способом полигонов профессора В.В. Попова
Вычисление высот точек по ходам, по уравненным превышениям
Оценка точности полученных результатов
Навигация
Выбор наилучших вариантов засечки
Уравнивание геодезических сетей сгущения упрощенным способом
30079
знаков
13
таблиц
2
изображения
2.3 Выбор наилучших вариантов засечки
Для выбора лучших вариантов засечки производятся те же действия, что и при прямой засечке:
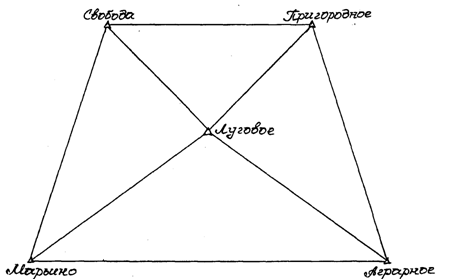
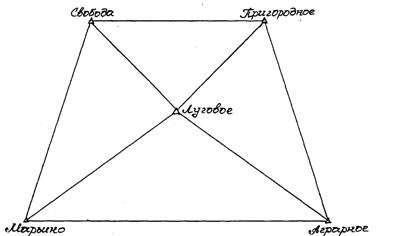
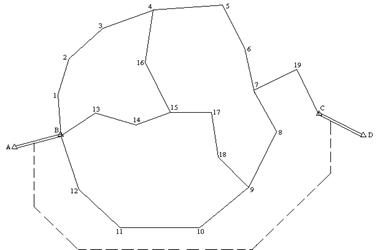
- строятся инверсионные треугольники (вершинами этих треугольников будут только конечные точки отрезков ri)
- визуально определяются треугольники с большими площадями, и именно они выбираются для решения обратной засечки.
В моем варианте были выбраны треугольники 3-4-1 и 3-4-2 для решения.
2.4 Решение наилучших вариантов засечки
Вычисление координат дополнительного пункта, определенного обратной многократной засечкой, приведены в табл. 4.
Таблица 4 - Схема для вычислений обратной угловой засечки.
| обозначение пунктов | координаты | - | ∆XBC | - | ΔYBC | |
| A | XA | YA | αAP | - | tg αAP | - |
| β2 | ∆XBC | ctg β2 | ΔYBC | |||
| B | XB | YB | αBP | - | tg αBP | - |
| β3 | ∆XCA | ctg β3 | ΔYCA | |||
| C | XC | YC | - | ∑ | - | ∑ |
| P | XP | YP | YP’ | ∆X0 | tg αAP - tg αBP | ΔY0 |
Для решения задачи сначала я определила дирекционный угол направления АР, принятого в качестве главного, по формуле Деламбра:
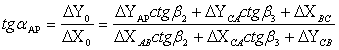(5),
далее определяем дирекционный угол следующего направления:
(6).
После того, как определила дирекционные углы направлений АР и ВР, вычислила координаты точки Р по формулам Гаусса:
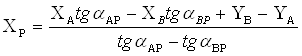(7)
(8)
Для контроля вычислений применила формулу:
(9).
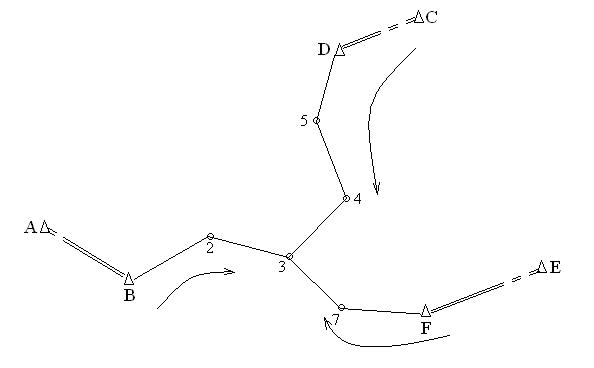
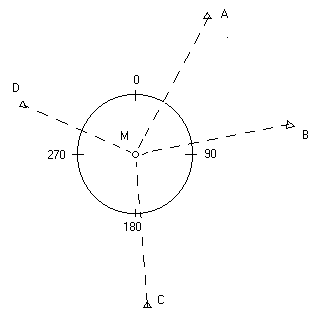
В формулах (5-9) обозначения соответствуют схеме, представленной на рисунке 2.
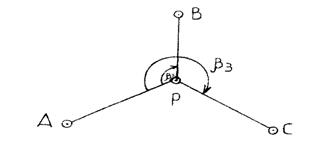
Рисунок 2 – Схема обозначений к вычислениям.
Решение задачи представлено в таблицах 5 и 6.
Таблица 5 – Решение обратной угловой засечки.
| Обозначение пунктов | координаты | - | -247,86 | - | 641,35 | |
| 3 (A) | 6653,66 | 2959,70 | 241 | - | 1,865475 | - |
| 95 | 699,51 | -0,102443 | 250,50 | |||
| 4 (B) | 7353,17 | 3210,20 | 337 | - | -0,411042 | - |
| 182 | -451,65 | 21,427930 | -891,85 | |||
| 1 (С) | 7150,31 | 3851,55 | - | 0 | - | 0 |
| P | 6890,00 | 3400,58 | 3400,58 | -10390,93 | 2,276517 | -19384,02 |
48’22”Таблица 6 – Решение обратной угловой засечки.
| Обозначение пунктов | координаты | - | -739,31 | - | 606,23 | |
| 3 (A) | 6653,66 | 2959,70 | 241 | - | 1,865398 | - |
| 95 | 699,51 | -0,102443 | 250,50 | |||
| 4 (B) | 7353,17 | 3210,20 | 337 | - | -0,411065 | - |
| 241 | 39,8 | 0,536601 | -856,73 | |||
| 2 (C) | 6613,86 | 3816,43 | - | 0 | - | 0 |
| P | 6890,01 | 3400,59 | 3400,59 | -656,53 | 2,276463 | -1224,69 |
48’18”Координаты в двух вариантах различны, но расхождения не превышают 0,2 м, за окончательные значения координат принимаем их средние значения:
Среднее Х=6890,005
Среднее Y=3400,585.
Похожие работы
... 1 5008,50 1000,00 1753,45 2748,03 2376,28 72 º28'50'' 101 º12'25'' 351 º18'32'' Луговое Аграрное Свобода 2. Уравновешивание систем ходов плановой съемочной сети 2.1 Уравновешивание систем теодолитных ходов с одной узловой точкой 2.1.1 Задание Произвести уравновешивание систем теодолитных ходов, сходящихся в узловой точке 3 и опирающихся ...
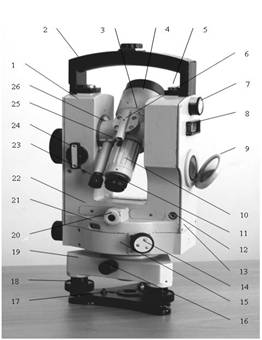
... с ценой деления 1 сек. Области применения: построение геодезических сетей сгущения (триангуляция 4 класса, полигонометрия IV класса), в прикладной геодезии (строительство, изыскания и т.д.), астрономо- геодезических измерениях (определение азимута по Солнцу и по Полярной Звезде). Модель 3Т5КП предназначена для измерения горизонтальных и вертикальных углов и не имеет микрометра. Области ...
... по формуле: ¦x=åDx-(xк-xн); ¦y=åDy-(yк-yн) сумма поправок приращений должна равнятся нулю. dxBC+dxCD+dXDE+¦x=0 dyBC+dyCD+dyDE+¦=0 4. Упрощенное уравнивание центральной системы. В центральной системе возникает условное уравнение фигур, горизонта и полюса. Математически эти условия выражаются уравнениями поправок. Число условных уравнений фигур ...
... в полосе съемке со смежных станций. В простейшем случае составление плана по результатам тахеометрической съемки начинают с построения координатной сетки и нанесению по координатам точек теодолитного хода. Правильность нанесения точек хода контролируют по длинам его сторон: измеряют расстояния между вершинами – выраженными в масштабе, они должны быть равны расстояниям между соответствующими ...
0 комментариев