Навигация
Оценка ожидаемой точности результатов
2.5 Оценка ожидаемой точности результатов
Далее я вычислила среднюю квадратическую ошибку положения определяемого пункта:
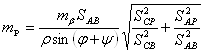 (10),
(10),
где ![]() - средняя квадратическая ошибка измерения углов (10''),
- средняя квадратическая ошибка измерения углов (10''),
S – расстояния, измеренные по схеме, м,
![]() =
=![]() ,
, ![]() - углы, измеряемые транспортиром по схеме.
- углы, измеряемые транспортиром по схеме.
Среднюю квадратическую ошибку координат, полученных как средние значения из двух вариантов, вычислила по формуле:
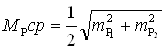 (11).
(11).
Из формулы (10) средняя квадратическая ошибка положения определяемого пункта:
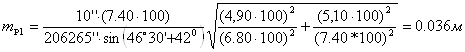
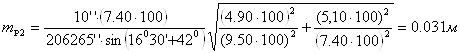
Из формулы (11) нашла среднюю квадратическую ошибку координат, полученных как средние значения из двух вариантов:
![]()
Итак, в этой задаче было решено два наилучших варианта засечки. Для решения задачи была построена схема расположения определяемого и исходных пунктов, выбраны наилучшие варианты засечки с помощью инверсионных треугольников, решены эти варианты засечки. Координаты пункта Р, полученные в двух вариантах, оказались в допуске и за окончательные значения координат были приняты их средние значения: среднее Х=6890,005 м, среднее Y=3400,585 м.
Вычисления были выполнены со следующими ошибками:
- средняя квадратическая ошибка положения определяемого пункта: mp1=0,036 м и mp2=0,031 м
- средняя квадратическая ошибка координат, полученных как средние значения из двух вариантов: МpСр=0,02 м
уравнивание геодезическая сеть сгущение засечка
3. Уравнивание ходов полигонометрии второго разряда, образующих одну узловую точку
3.1 Общие указания и исходные данные
ПОЛИГОНОМЕТРИЯ (от греч. polygonos - многоугольный и ...метрия), метод определения взаимного положения точек земной поверхности для построения опорной геодезической сети путем измерения длин прямых линий, связывающих эти точки, и горизонтальных углов между ними. Применяется в залесенной и застроенной местности вместо триангуляции.
Наилучший результат получается при совместном уравнивании всех измеренных величин. Число измерений в полигонометрической сети велико, измеренные величины разнородны (углы и расстояния), сеть имеет сложную форму. Строгое уравнивание на практике выполняется чрезвычайно редко, так как представляет собой сложную и трудоёмкую задачу.
Задача уравнивания значительно облегчается при последовательном несовместном уравнивании. При этом сначала уравнивают углы, а затем приращения координат (абсцисс и ординат). Полученные таким образом результаты будут отличаться от результатов строгого уравнивания полигонометрической сети.
Заданием предусмотрено выполнить уравнивание системы ходов раздельным способом.
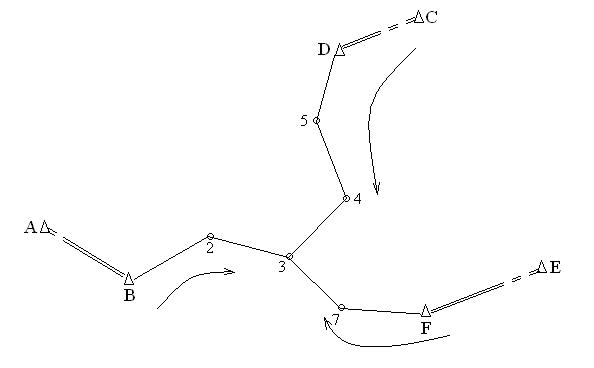
3.2 Вычисление координат исходных пунктов и дирекционных углов исходных направлений
По данным, изменённым в соответствии с порядковым номером, я вычислила координаты исходных пунктов и дирекционные углы исходных направлений. Вычисление произвела в таблице 7.
Таблица 7 – Данные по исходным пунктам.
пункт | углы | дирекционные углы | Сторона, м | Координаты, м | |||||
| град. | мин. | сек. | град. | мин. | сек. | X | Y | ||
| A | 43 | 54 | 55 | 2349486,73 | 9475377,12 | ||||
| 144 | 17 | 33 | 3301,47 | ||||||
| B | 103 | 52 | 34 | 2346805,92 | 9477304,01 | ||||
| 220 | 24 | 59 | 4296,16 | ||||||
| C | 32 | 12 | 31 | 2343535,03 | 9474518,65 | ||||
| 8 | 12 | 28 | 6013,30 | ||||||
| A | 43 | 54 | 55 | 2349486,73 | 9475377,12 | ||||
| 144 | 17 | 33 | |||||||
Дирекционные углы направлений ВС, СА были вычислены по формуле:
![]() (12),
(12),
приращения координат:
![]() и
и ![]() (13),
(13),
координаты исходных пунктов:
![]() и
и ![]() (14).
(14).
Похожие работы
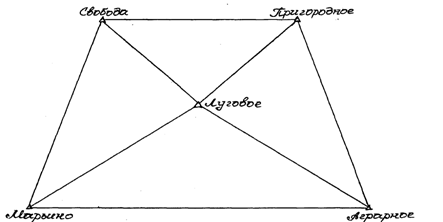
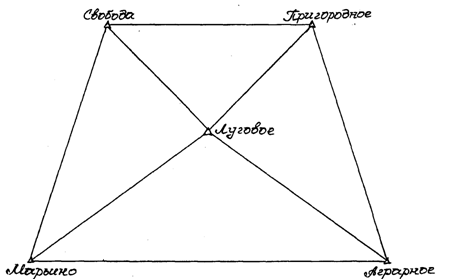
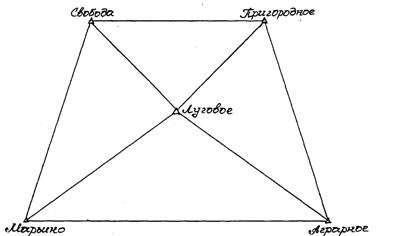
... 1 5008,50 1000,00 1753,45 2748,03 2376,28 72 º28'50'' 101 º12'25'' 351 º18'32'' Луговое Аграрное Свобода 2. Уравновешивание систем ходов плановой съемочной сети 2.1 Уравновешивание систем теодолитных ходов с одной узловой точкой 2.1.1 Задание Произвести уравновешивание систем теодолитных ходов, сходящихся в узловой точке 3 и опирающихся ...
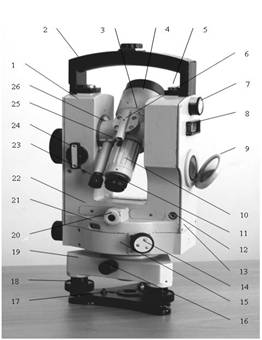
... с ценой деления 1 сек. Области применения: построение геодезических сетей сгущения (триангуляция 4 класса, полигонометрия IV класса), в прикладной геодезии (строительство, изыскания и т.д.), астрономо- геодезических измерениях (определение азимута по Солнцу и по Полярной Звезде). Модель 3Т5КП предназначена для измерения горизонтальных и вертикальных углов и не имеет микрометра. Области ...
... по формуле: ¦x=åDx-(xк-xн); ¦y=åDy-(yк-yн) сумма поправок приращений должна равнятся нулю. dxBC+dxCD+dXDE+¦x=0 dyBC+dyCD+dyDE+¦=0 4. Упрощенное уравнивание центральной системы. В центральной системе возникает условное уравнение фигур, горизонта и полюса. Математически эти условия выражаются уравнениями поправок. Число условных уравнений фигур ...
... в полосе съемке со смежных станций. В простейшем случае составление плана по результатам тахеометрической съемки начинают с построения координатной сетки и нанесению по координатам точек теодолитного хода. Правильность нанесения точек хода контролируют по длинам его сторон: измеряют расстояния между вершинами – выраженными в масштабе, они должны быть равны расстояниям между соответствующими ...




0 комментариев