Выбор наилучших вариантов засечки
Оценка ожидаемой точности полученных результатов
Выбор наилучших вариантов засечки
Оценка ожидаемой точности результатов
Вычисление и уравнивание дирекционного угла узловой стороны
Вычисление и уравнивание координат узловой точки
Уравнивание ходов технического нивелирования способом полигонов профессора В.В. Попова
Вычисление высот точек по ходам, по уравненным превышениям
Оценка точности полученных результатов
Навигация
Вычисление высот точек по ходам, по уравненным превышениям
Уравнивание геодезических сетей сгущения упрощенным способом
30079
знаков
13
таблиц
2
изображения
4.3 Вычисление высот точек по ходам, по уравненным превышениям
Далее, т.к. контроль выполнился, вычислила уравненные превышения между точками нивелирования и высоты точек по каждому ходу. Поправки в измеренные превышения нашла, распределяя поправку на ход пропорционально числу станций между точками нивелирования.
Таблица 11 - Измеренные величины и результаты уравнивания
| № хода | № точки | длина хода, Li, км | число станций | Превы шения, м | Поправки, мм | уравненные | |
| Превышения, м | Высоты, м | ||||||
| 1 | 2 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | Rp1 | 106,973 | |||||
| 1 | 4,8 | 29 | -3,979 | +5 | -3,974 | 102,999 | |
| 2 | 7,1 | 35 | -1,251 | +6 | -1,245 | 101,754 | |
| ∑ | 11,9 | 64 | -5,23 | +11 | -5,219 | ||
| 2 | 2 | 101,754 | |||||
| 3 | 6,3 | 36 | -1,098 | +2 | -1,096 | 100,658 | |
| 4 | 7 | 37 | -2,002 | +2 | -2,000 | 98,658 | |
| ∑ | 13,3 | 73 | -3,1 | +4 | -3,096 | ||
| 3 | 4 | 98,658 | |||||
| 5 | 5,3 | 26 | 8,953 | +1 | +8,954 | 107,612 | |
| 6 | 5 | 28 | -5,092 | +1 | -5,091 | 102,521 | |
| 7 | 4,8 | 26 | -0,858 | 0 | -0,858 | 101,663 | |
| ∑ | 15,1 | 80 | 3,005 | +2 | +3,005 | ||
| 4 | 7 | 101,663 | |||||
| 8 | 7,4 | 33 | -1,038 | -3 | -1,041 | 100,622 | |
| Rp1 | 6,1 | 28 | 6,353 | -2 | +6,351 | 106,973 | |
| ∑ | 13,5 | 61 | 5,315 | -5 | +5,310 | ||
| 5 | 2 | 101,754 | |||||
| 9 | 7,8 | 41 | -3,186 | +6 | -3,180 | 98,574 | |
| 10 | 6,7 | 30 | 7,461 | +4 | +7,465 | 106,039 | |
| 11 | 6,5 | 38 | 15,617 | +5 | +15,622 | 121,661 | |
| 12 | 6,8 | 28 | -16,824 | +4 | -16,820 | 104,841 | |
| ∑ | 27,8 | 137 | 3,068 | +19 | +3,087 | ||
| 6 | 12 | 104,841 | |||||
| 13 | 7 | 36 | 7,299 | +1 | +7,300 | 112,141 | |
| ∑ | 7 | 36 | 7,299 | +1 | +7,300 | ||
| 7 | 13 | 112,141 | |||||
| 4 | 5,7 | 25 | -13,481 | -2 | -13,483 | 98,658 | |
| ∑ | 5,7 | 25 | -13,481 | -2 | -13,483 | ||
| 8 | 12 | 104,841 | |||||
| 14 | 10,6 | 54 | 4,811 | +10 | +4,821 | 109,662 | |
| ∑ | 10,6 | 54 | 4,811 | +10 | +4,821 | ||
| 9 | 14 | 109,662 | |||||
| 13 | 7,1 | 28 | 2,480 | -1 | +2,479 | 112,141 | |
| ∑ | 7,1 | 28 | 2,480 | -1 | +2,479 | ||
| 10 | 14 | 109,662 | |||||
| 15 | 5,4 | 29 | -7,899 | +6 | -7,893 | 101,769 | |
| 16 | 5,6 | 28 | 3,885 | +6 | +3,891 | 105,660 | |
| Rp2 | 6,5 | 32 | -5,536 | +8 | -5,528 | 100,132 | |
| ∑ | 17,5 | 89 | -9,55 | +20 | -9,530 | ||
| 11 | Rp2 | 100,132 | |||||
| 17 | 6,8 | 38 | 1,066 | -4 | +1,062 | 101,194 | |
| 7 | 6,8 | 25 | 0,472 | -3 | +0,469 | 101,663 | |
| ∑ | 13,6 | 63 | 1,538 | -7 | +1,531 | ||
В результате уравнивания я определила высоты всех точек. Для контроля использовала известные высоты Rp1=106.973 м, Rp2=100,132 м.
Похожие работы
... 1 5008,50 1000,00 1753,45 2748,03 2376,28 72 º28'50'' 101 º12'25'' 351 º18'32'' Луговое Аграрное Свобода 2. Уравновешивание систем ходов плановой съемочной сети 2.1 Уравновешивание систем теодолитных ходов с одной узловой точкой 2.1.1 Задание Произвести уравновешивание систем теодолитных ходов, сходящихся в узловой точке 3 и опирающихся ...
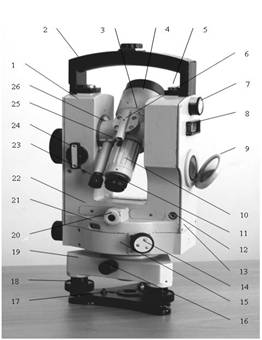
... с ценой деления 1 сек. Области применения: построение геодезических сетей сгущения (триангуляция 4 класса, полигонометрия IV класса), в прикладной геодезии (строительство, изыскания и т.д.), астрономо- геодезических измерениях (определение азимута по Солнцу и по Полярной Звезде). Модель 3Т5КП предназначена для измерения горизонтальных и вертикальных углов и не имеет микрометра. Области ...
... по формуле: ¦x=åDx-(xк-xн); ¦y=åDy-(yк-yн) сумма поправок приращений должна равнятся нулю. dxBC+dxCD+dXDE+¦x=0 dyBC+dyCD+dyDE+¦=0 4. Упрощенное уравнивание центральной системы. В центральной системе возникает условное уравнение фигур, горизонта и полюса. Математически эти условия выражаются уравнениями поправок. Число условных уравнений фигур ...
... в полосе съемке со смежных станций. В простейшем случае составление плана по результатам тахеометрической съемки начинают с построения координатной сетки и нанесению по координатам точек теодолитного хода. Правильность нанесения точек хода контролируют по длинам его сторон: измеряют расстояния между вершинами – выраженными в масштабе, они должны быть равны расстояниям между соответствующими ...
0 комментариев