Навигация
Х ³ 2. Неравенство то же, что и в случае 2. Подходит лишь х = 2
4. х ³ 2. Неравенство то же, что и в случае 2. Подходит лишь х = 2.
Ответ: £ х £ 2.
Пример: Решить неравенство.
½½х3 + х - 3½- 5½£ х3 – х + 8.
Решение. Решим это неравенство не стандартным образом.
![]()
![]() ½х3 + х - 3½ - 5 £ х3 – х + 8, ½х3 + х - 3½ £ х3 – х + 13
½х3 + х - 3½ - 5 £ х3 – х + 8, ½х3 + х - 3½ £ х3 – х + 13
½х3 + х - 3½ - 5 £ -х3 + х – 8 ½х3 + х - 3½ ³ - х3 + х – 3
![]()
![]()
![]()
![]() х3 + х – 3 £ х3 – х + 13 х £ 8,
х3 + х – 3 £ х3 – х + 13 х £ 8,
![]()
![]()
![]()
![]() х3 + х – 3 ³ -х3 + х – 13, х3 ³ -5,
х3 + х – 3 ³ -х3 + х – 13, х3 ³ -5,
![]() х3 + х – 3 ³ -х3 + х – 3, х3 ³ 0,
х3 + х – 3 ³ -х3 + х – 3, х3 ³ 0,
х3 + х – 3 £ х3 – х + 3 х £ 3
![]()
![]()
![]() -£ х £ 8, -£ х £ 8.
-£ х £ 8, -£ х £ 8.
х – любое
Ответ: -£ х £ 8.
Неравенства с параметрами.
Неравенства с параметрами являются наиболее трудными задачами курса элементарной математики. Это объясняется тем, что их решения следует получать при всех допустимых значениях входящих в них параметров.
Пример: Для всех значений а решить неравенство
aх > 1/x.
Решение: Запишем неравенство в виде
> 0,
тогда исходное неравенство эквивалентно двум системам неравенств:
ax2 – 1 > 0, ax2 – 1 < 0,
x > 0; x < 0.
Рассмотрим первую систему. Первое неравенство запишем в виде:
ax2 > 1.
При а > 0 оно эквивалентно неравенству х2 > 1/a, множество решений которого х < -1/ и x > 1/. В этом случае решения первой системы: хÎ(1/; ¥). При а £ 0 левая часть неравенства ах2 –1 > 0 отрицательна при любом х и неравенство решений не имеет, а следовательно, не имеет решений и вся система неравенств.
Рассмотрим вторую систему. При а > 0 решениями неравенства ах2 – 1<0 будут значения хÎ(-1/; 1/), а решениями системы ¾ значения хÎ(-1/; 0). При a£ 0 левая часть неравенства ах2 –1 < 0 отрицательна при
|
|
 |
любых значениях х, т.е. это неравенство выполняется при все хÎR и, следовательно, решениями системы будут значения хÎ(-¥; 0).
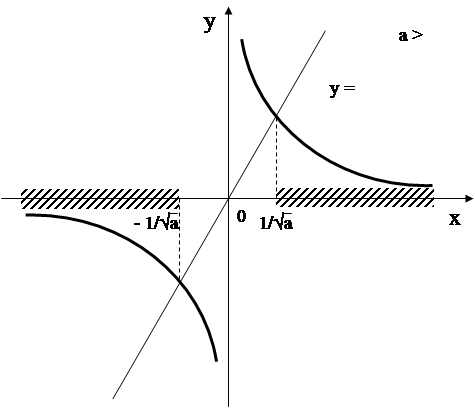 |
Приведем графическую иллюстрацию решения этого примера.
Для этого рассмотрим отдельно два случая а > 0 и а £ 0 и для каждого из них построим графики функций, стоящих в левой и правой частях исходного неравенства. Заштрихованные промежутки оси Ох представляют собой решение неравенства в рассматриваемых случаях.
Графическая иллюстрация облегчает решение уравнений и неравенств с параметрами.
Ответ: Если а £ 0, то хÎ(-¥; 0); если а > 0, то хÎ(-1/; 0)È(1/; ¥).
Пример: Решить неравенство:
¾ < .
Решение: Преобразуем данное неравенство: 3m2х + 3 – 2mx2 – 6 < m + 9x; mx2 – 9x < m + 3; (m – 3)(m + 3)x < m + 3. Далее находим решение неравенства при различных значения параметра m:
1) Пусть (m – 3)(m + 3) > 0, т.е. m < -3 или m > 3. Тогда неравенство имеет решение х < 1/(m – 3).
2) Пусть (m – 3)(m + 3) < 0, т.е. –3 < m < 3. Тогда неравенство имеет решение х > 1/(m – 3).
3) Пусть (m – 3)(m + 3) = 0, т.е. m = 3 или m = -3. Тогда если m = 3, то неравенство примет вид 0×х < 6 и, значит выполняется при любом хÎR. Если же m = -3, то неравенство примет вид 0×х < 0 и, следовательно, не имеет решении.
Пример: Для каждого неотрицательного значения параметра а решить неравенство
4а3х4 + 4а2х2 + 32х + а + 8 ³ 0.
Решение. Левая часть неравенства представляет собой многочлен как относительно х, так и относительно параметра а. Степени соответственно равны 4 и 3. Однако если умножить многочлен на а, а затем сделать замену y = ax, то в новом многочлене максимальная степень параметра а будет равна 2. Случай а = 0 дает нам ответ х ³ - ¼. Будем теперь считать, что а > 0. Умножив обе части неравенства на а и сделав замену y = ax, получим
4y4 + 4ay2 + 32y + a2 + 8a ³ 0.
Левая часть представляет собой квадратный трехчлен относительно а:
a2 + (4y2 + 8)a + 4y2 + 32y ³ 0,
¼D = (2y2 + 4) 2 – 4y2 – 32y = 16(y – 1) 2.
Раскладывая левую часть неравенства на множители, получим
(а + 2y2 + 4y)(a + 2y2 – 4y + 8) ³ 0,
или
(2y2 + 4y + a)(2y2 – 4y + 8 + a) ³ 0.
Второй множитель положителен при всех y, если а > 0. Приходим к неравенству 2y2 + 4y + a ³ 0, откуда, если 0 < a < 2, y £ ½(-2 -) или y ³ ½(-2+); если а ³ 2, y – любое. Возвращаясь к х, получим ответ.
Ответ: Если а = 0, то х ³ - ¼; если 0 < a < 2, то х £ 1/2a*(-2 - ) или х ³ 1/2a(-2 + ); если а ³ 2, то х – любое.
|
![]() х2 – 3х + 2 £ 0,
х2 – 3х + 2 £ 0,
ах2 – 2(а + 1)х + а – 1 ³ 0.
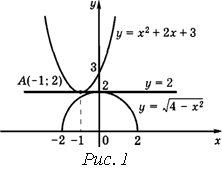
Решение: Поскольку решением первого неравенства является 1 £ х £ 2, то задача сводится (при а ¹ 0) к выяснению расположения корней квадратного трехчлена f(x) = ах2 – 2(а + 1)х + а –1 относительно отрезка [1; 2]. Имеем
¼D = (а + 1) 2 – а(а – 1) = 3а + 1, f(1) = -3, f(2) = а – 5.
Область изменения параметра а оказалось разделенной на 4 части (не считая граничных точек).
1) Если а < - 1/3, второе неравенство, а следовательно и данная система не имеют решения. То же имеет место и при а = -1/3.
2)
|

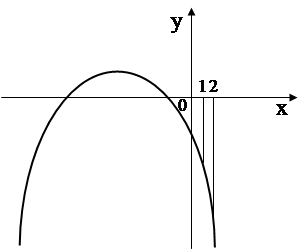
Если –1/3 < a < 0, то f(1) < 0, f(2) < 0. Для вершины параболы выполняется неравенство хв = < 0 (рис. 1,а ). Следовательно, множество решении второго неравенства не содержит точек отрезка [1; 2]. Система
не имеет решения. То же имеет место и при а = 0.
3) Если 0 < a < 5, то f(1) < 0, f(2) < 0 (рис. 1, б). Значит, на всем отрезке [1; 2] f(x) < 0. Система вновь не имеет решения.
4)  Если а ³ 5, то f(1) < 0, f(2) ³ 0 (рис. 1, в). Решением системы будет х2 £ х £ 2 где х2 – больший корень уравнения f(x) = 0.
Если а ³ 5, то f(1) < 0, f(2) ³ 0 (рис. 1, в). Решением системы будет х2 £ х £ 2 где х2 – больший корень уравнения f(x) = 0.
|
Пример: Решить неравенство
½2х2 + х – а - 8½ £ х2 + 2х – 2а – 4.
Решить: Напомним, что неравенство ½а½ £ b эквивалентно двойному неравенству –b £ a £ b. В нашем случае после преобразования приходим к системе неравенств
![]() а £ -х2 + х + 4,
а £ -х2 + х + 4,
а £ х2 + х – 4.
Изобразим на плоскости (х; а) множество точек, координаты которых удовлетворяют полученной системе. При конкретном значении параметра а = a решением нашего неравенства будут абциссы тех точек горизонтальной прямой а = a, которые находятся в заштрихованной области. Найдем точки пересечения А(2; 2), В(-2; -2) наших точек парабол и вершину С(-0,5; -4,25) параболы а = х2 +х – 4.
Далее получаем: если а > 2, то соответствующая прямая пересекается с заштрихованной областью.
Если –2 < a £ 2, то соответствующая прямая пересекается с заштрихованной областью по отрезку. Концами этого отрезка будут точки с абциссами ½(-1 + ) (больший корень уравнения а = х2 + х – 4 или х2 – х – 4 + а= 0).
Если –4¼ £ a £ -2, то горизонтальная прямая, соответствующая таким а, пересекается с заштрихованной областью по двум отрезкам. Решением неравенства будет
½(1 - ) £ х £ - ½(1 + ),
½(-1 + ) £ х £ -½(1 + ).
Если а < -4¼, то ½(1 - ) £ x £ ½(1 + ).
Системы рациональных неравенств.
Пусть надо найти числовые значения х, при которых превращаются в верные числовые неравенства одновременно несколько рациональных неравенств. В таких случаях говорят, что надо решить систему рациональных неравенств с одним неизвестным х.
Чтобы решить систему рациональных неравенств, надо найти все решения каждого неравенства системы. Тогда общая часть всех найденных решений и будет решением системы.
Пример: Решить систему неравенств
![]()
(х –1)(х – 5)(х – 7) < 0,
> 0.
Сначала решаем неравенство
(х – 1)(х – 5)(х – 7) < 0.
Применяя метод интервала (рис. 1), находим, что множество всех решении неравенства (2) состоит из двух интервалов: (-¥, 1) и (5, 7).
Теперь решим неравенство
> 0.
Применяя метод интервалов (рис. 2), находим, что множество всех решении неравенства (3) также состоит их двух интервалов: (2, 3) и (4, +¥).
Теперь надо найти общую часть решении неравенств (2) и (3). Нарисуем координатную ось х и отметим на ней найденные решения. Теперь яс
 |
но, что общей частью решении неравенств (2) и (3) является интервал (5, 7) (рис. 3).
Следовательно, множество всех решении системы неравенств (1) составляет интервал (5, 7).
Пример: Решить систему неравенств
![]() х2 – 6х + 10 < 0,
х2 – 6х + 10 < 0,
> 0.
Решим сначала неравенство
х2 – 6х + 10 < 0.
Применяя метод выделения полного квадрата, можно написать, что
х2 – 6х + 10 = х2 - 2×х×3 + 32 - 32 + 10 = (х – 3) 2 +1.
Поэтому неравенство (2) можно записать в виде
(х – 3) 2+ 1 < 0,
откуда видно, что оно не имеет решении.
Теперь можно не решать неравенство
> 0,
так как ответ уже ясен: система (1) не имеет решении.
Пример: Решить систему неравенств
![]() < 1,
< 1,
x2 < 64.
Рассмотрим сначала первое неравенство; имеем
- 1 < 0, < 0.
С помощью кривой знаков (рис. 4) находим решения этого неравенства: х < -2; 0 < x < 2.
Решим теперь второе неравенство заданной системы. Имеем x2 - 64 < 0, или (х – 8)(х + 8) < 0. С помощью кривой знаков (рис. 5) находим решения неравенства: -8 < x < 8.
Отметив найденные решения первого и второго неравенства на общей числовой прямой (рис. 6), найдем такие промежутки, где эти решения совпадают (пресечение решении): -8 < x < -2; 0 < x < 2. Это и есть решение системы.
Пример: Решить систему неравенств
![]() х2 ³ 100х3;
х2 ³ 100х3;
³ 0.
Преобразуем первое неравенство системы:
х3(х – 10)(х + 10) ³ 0, или х(х – 10)(х + 10) ³ 0
(т.к. множители в нечетных степенях можно заменять соответствующими множителями первой степени); с помощью метода интервалов (рис. 7) найдем решения последнего неравенства: -10 £ х £ 0, х ³ 10.
Рассмотрим второе неравенство системы; имеем
£ 0.
Находим (рис. 8) х £ -9; 3 < x < 15.
Объединив найденные решения, получим (рис. 9) х £ 0; х > 3.
Пример: Найти целочисленные решения системы неравенств:
![]() х + y < 2,5,
х + y < 2,5,
x – y > -3,
y –1 > 0.
Решение: Приведем систему к виду
![]() x + y < 2,5,
x + y < 2,5,
y – x < 3,
y > 1.
Складывая первое и второе неравенства, имеем y < 2, 75, а учитывая третье неравенство, найдем 1 < y < 2,75. В этом интервале содержится только одно целое число 2. При y = 2 из данной системы неравенств получим
![]() х < 0,5,
х < 0,5,
x > -1,
откуда –1 < x < 0,5. В этом интервале содержится только одно целое число 0.
Ответ: х = 0, y =2.
ГРАФИЧЕСКОЕ РЕШЕНИЕ НЕРАВЕНСТВ
Неравенства с одной или двумя переменными можно решать графически.
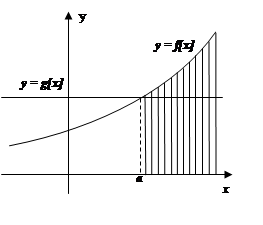
Неравенство с одной переменой можно записать так: f(x) > g(x), где f(x) и g(x) – выражения, содержащие переменную.
Построим в одной системе координат графики функций y = f(x) и у = g(x).
 Решение неравенства есть множество значений переменой х, при которых график функций у=g(x), так как f(x)>g(x).Это показано на рисунках 1 и 2.
Решение неравенства есть множество значений переменой х, при которых график функций у=g(x), так как f(x)>g(x).Это показано на рисунках 1 и 2.
 |
Решение неравенства с двумя переменными f(x,y)>0 есть множество
точек плоскости, координаты которых удовлетворяют этому неравенству. Рассмотрим на примерах решение некоторых неравенств с двумя переменными.
 Пример 1. Решить графически неравенство
Пример 1. Решить графически неравенство
x + у > 0.
Решение. Запишем неравенство в виде у> -х. Построим прямую у= -х. Координаты точек плоскости, которые лежат выше этой прямой, есть решение неравенства ( на рисунке 3 – заштрихованная область).
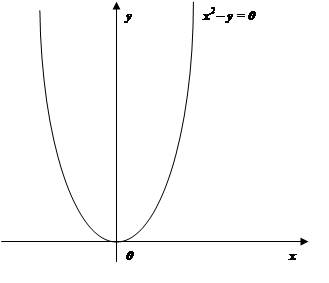 Пример 2. Решить графически неравенство
Пример 2. Решить графически неравенство
х2 – у > 0.
Решение. Запишем неравенство в виде у < x2 .
Построим кривую у = х2 (парабола) (рисунок 4).
Решение неравенства есть координаты точек плоскости, которые лежат в заштрихованной области (ниже построенной параболы).
При решении систем неравенств с двумя переменными находят пересечение областей решений этих неравенств.
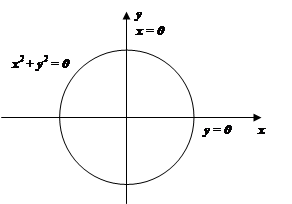
Пример 3.Решить графически систему неравенств
![]()
x2 + у2 – 4 > 0,
y > 0,
x > 0.
Решение. Решение первого неравенства системы есть координаты точек плоскости (рисунок 5), которые лежат вне окружности х+у=4; решение второго неравенства есть координаты точек верхней полуплоскости; решение третьего неравенства есть координаты точек правой полуплоскости.
Решением системы являются координаты точек, которые лежат в заштрихованной области.
ТЕСТ
1) Решить уравнение: = 1.
А) 0,
Б) 1,
В) Нет решений,
Г) xÎ (-¥; 1)È(1; ¥).
2) Решить уравнение: = 0.
А ) Нет решений,
Б) -1,
В) -5,
Г) -1; -5.
3) Решить уравнение: + - = 0.
А) -2; ; 5,
Б) Нет решений,
В) xÎ (-¥; 3)È(3; ¥),
Г) x ÎR.
4) Решить уравнение: ax = 1.
А) Если a ¹ 0, то xÎR; если a = 0, то нет решений,
Б) Если a = 0, то нет решений; если a ¹ 0, то x = ,
В) Если a = 0 , то xÎR; если a ¹ 0, то x = .
Г) Нет решений.
5) При каких a уравнение ax2 - 4x + a + 3 = 0 имеет более одного корня?
А) - 4 < a < 0,
Б) 0 < a < 1,
В) aÎ(-¥; 0)È(0; ¥),
Г) - 4 < a < 0; 0 < a < 1.
6) При каких a уравнение (a - 2)x2 + (4 - 2a)x + 3 = 0 имеет единственное решение?
А) 2,
Б) аÎ(-¥; 2)È(2; ¥),
В) 5,
Г) - 4.
7) Решить уравнение: |x2 - 1| + |a(x - 1)| = 0.
А) Если a ¹ 0, то x =1; если a = 0, то x = ±1,
Б) Если а ¹ 0, то нет решений; если a = 0, то x = 1.
В) x = ±1,
Г) Нет решений.
8) ![]() Решить систему:
Решить систему:
- = ,
y2 - x - 5 = 0.
А) (4; 3), (4; - 3),
Б) (1; 2),
В) Нет решений,
Г) xÎR, y = ±3.
9) ![]() Решить систему:
Решить систему:
x2 + y2 - 2x = 0,
x2 - 2xy + 1 = 0.
А) (1; -1), (5; 5)
Б) Нет решений,
В) (1;1),
Г) (-2; 3), (3; -2).
10) При каких a неравенство 2x + a > 0 является следствием неравенства x + 1 - 3a > 0?
А) ,
Б) а ³ ,
В) при любых a,
Г) а £ .
11) Найти наибольшее целое х, удовлетворяющие неравенству:
- > 1.
а) хÎ(-¥; -3,5),
б) –3,
в) –4,
г) нет решений.
12) Найти наибольшее целое х, удовлетворяющие неравенству:
- > -.
а)5,
б) –3,
в) 4,
г)нет решений.
13) Найти целочисленные решения неравенств:
< 0.
а) 0, 1, 2,
б) 4, 5,
в) 7,
г)нет решений.
14) Найти целочисленные решения неравенств:
![]()
17 – 4х < 0,
10х – 67 < 0.
а)5,
б) –3, -4, -5,
в) 5,6,
г)нет решений.
15) Решить неравенство:
- < 0.
а) (-¥; -3)È(0; 3,
б) (–3, 0)È(0; ¥),
в) (5; 7),
г) нет решений.
16) Решить неравенство:
< -.
а) (-¥; -3/25)È(0; ¥),
б) (–12, 0)È(7;9),
в) (-¥;)È ( ; 5),
г) нет решений.
17) Решить неравенство:
< -1.
а) (-9; -5)È(0; 8),
б) (–8, -7)È(1;3),
в) (-¥; -7)È(1; 3),
г) нет решений.
18) Решить неравенство:
£ .
а) [-4; -2)È(0;5],
б) (–1, 0]È[1;7),
в) (-4; -3)È[5; 7],
г) нет решений.
19) Решить неравенство
½1,5 – 3х½ < 3.
а) (-2,5; -2)È(0; 3,5],
б) (–0,5; 1,5),
в) (-4,5; -3,5),
г) нет решений.
20) Решить неравенство:
> ½х + 2½.
а) (-3; -1),
б) (0; 1),
в) (-7; -10),
г) нет решений.
Ответы: 1 - Г; 2 - В; 3 - В; 4 - Б; 5 - Г; 6 - В; 7 - А; 8 - А; 9 - В;10 – Б;
11 – В; 12 – А; 13 – А; 14 – В; 15 – А; 16 – В; 17 – Б; 18 – В; 19 – Б; 20 – А.
Список использованной литературы:
1) Математика. Интенсивный курс подготовки к экзамену. О. Ю. Черкасов, А. Г. Якушев. Москва, изд. “Айрис”, 1997.
2) Тысяча и один пример. Равенства и неравенства. А. М. Назаренко, Л. Д. Назаренко. Сумы, изд. “Слобожанщина”, 1994.
3) Система тренировочных задач и упражнений по математике. А. Я. Симонов. Москва, изд. “Просвещение” 1991.
4) Алгебра 8 класс. Н. Я. Виленкин. Москва, изд. “Просвещение”, 1995.
5) Задачи по математике для поступающих во ВТУЗы. Р. Б. Райхмист. Москва, изд. “Высшая школа”, 1994.
6) Алгебраический тренажёр. А. Г. Мерзляк. Москва - Харьков, изд. “Илекса”, изд. “Гимназия”, 1998.
7) Готовимся к экзамену по математике. Д. Т. Письменный. Москва, изд. “Айрис”, 1996.
8) Задачи по математике. Уравнения и неравенства. Вавилов В. В., Мельников И. И. Москва, изд. “Наука”, 1987.
9) Алгебра и начала анализа. Издание второе, переработанное и дополненное. А. Г. Мордкович. Москва, изд. “Высшая школа”, 1987.
10) Алгебра. Пособие для самообразования. С. М. Никольский. Москва, изд. “Наука”, 1985.
11) Справочник по методам решения задач по математике. А. Г. Цыпкин. Москва, изд. “Наука”, 1989.
12) Решение задач. И. Ф. Шарыгин. Москва, изд. “Просвещение”, 1994.
13) Алгебра и математический анализ. 10 класс. Н. Я. Виленкин. Москва, изд. “Просвещение”, 1997.
14) Математика. Алгебра и начала анализа. А. И. Лобанова. Киев, изд. “Вища школа”, 1987.
15) Алгебра. 9 класс. Н. Я. Виленкин. Москва, изд. “Просвещение”, 1996.
Похожие работы
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
... функция является знакопостоянной. Вычисляя, например, , получаем, что функция принимает только положительные значения. Ответ. . Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих ...
... курс «Решение уравнений и неравенств с использованием свойств функций» Глава II. Разработка элективного курса «Решение уравнений и неравенств с использованием свойств функций» §1. Методические основы разработки элективного курса Пояснительная записка. Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и ...
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
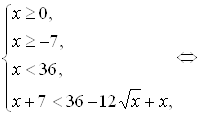
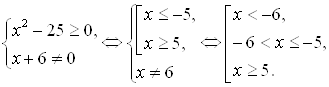
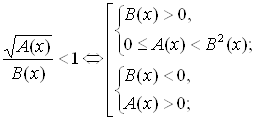
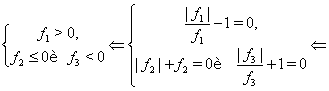
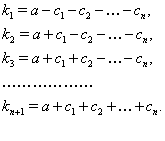
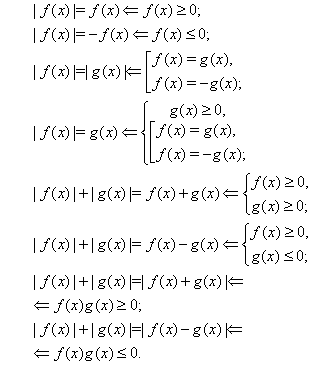
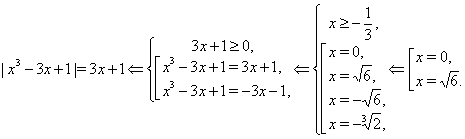





0 комментариев