Навигация
Не коррелированна с к-1 предыдущими главными компонентами
3. не коррелированна с к-1 предыдущими главными компонентами,
4. среди всех возможных комбинаций исходных признаков, которые не
не коррелированны с к-1 предыдущими главными компонентами, эта комбинация имеет наибольшую дисперсию.
Введём ортогональную матрицу U и перейдём от переменных Х к переменным Z, причём
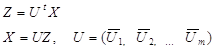
Вектор ![]() выбирается т. о., чтобы дисперсия
выбирается т. о., чтобы дисперсия ![]() была максимальной. После получения
была максимальной. После получения ![]() выбирается
выбирается ![]() т. о., чтобы дисперсия
т. о., чтобы дисперсия ![]() была максимальной при условии, что
была максимальной при условии, что ![]() не коррелированно с
не коррелированно с ![]() и т. д.
и т. д.
Так как признаки измерены в несопоставимых величинах, то удобнее будет перейти к центрированно-нормированным величинам. Матрицу исходных центрированно-нормированных значений признаков найдем из соотношения:
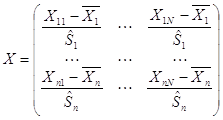 ,
,
где 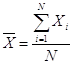 - несмещенная, состоятельная и эффективная оценка математического ожидания,
- несмещенная, состоятельная и эффективная оценка математического ожидания,
![]() -несмещенная, состоятельная и эффективная оценка дисперсии.
-несмещенная, состоятельная и эффективная оценка дисперсии.
Матрица наблюденных значений исходных признаков приведена в Приложении.
Центрирование и нормирование произведено с помощью программы"Stadia".
Так как признаки центрированы и нормированы, то оценку корреляционной матрицы можно произвести по формуле:
![]()
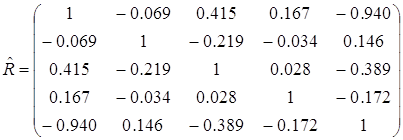
![]() .
.
Перед тем как проводить компонентный анализ, проведем анализ независимости исходных признаков.
Проверка значимости матрицы парных корреляций с помощью критерия Уилкса.Выдвигаем гипотезу:
Н0: ![]() незначима
незначима
Н1: ![]() значима
значима
Строим статистику ![]() , распределена по закону
, распределена по закону ![]() с
с ![]() степенями свободы.
степенями свободы.
![]() =125,7;
=125,7; ![]() (0,05;3,3) = 7,8
(0,05;3,3) = 7,8
т.к ![]() >
>![]() , то гипотеза Н0 отвергается и матрица является значимой, следовательно, имеет смысл проводить компонентный анализ.
, то гипотеза Н0 отвергается и матрица является значимой, следовательно, имеет смысл проводить компонентный анализ.
Проверим гипотезу о диагональности ковариационной матрицы
Выдвигаем гипотезу:
Н0: соv![]() =0,
=0, ![]()
Н1: соv![]()
Строим статистику ![]() , распределена по закону
, распределена по закону ![]() с
с ![]() степенями свободы.
степенями свободы.
![]() =123,21,
=123,21, ![]() (0,05;10) =18,307 т.к
(0,05;10) =18,307 т.к ![]() >
>![]() то гипотеза Н0 отвергается и имеет смысл проводить компонентный анализ.
то гипотеза Н0 отвергается и имеет смысл проводить компонентный анализ.
Для построения матрицы факторных нагрузок необходимо найти собственные числа матрицы ![]() , решив уравнение
, решив уравнение![]() .
.
Используем для этой операции функцию eigenvals системы MathCAD, которая возвращает собственные числа матрицы:
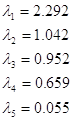
Т.к. исходные данные представляют собой выборку из генеральной совокупности, то мы получили не собственные числа ![]() и собственные вектора матрицы, а их оценки. Нас будет интересовать на сколько “хорошо” со статистической точки зрения выборочные характеристики описывают соответствующие параметры для генеральной совокупности.
и собственные вектора матрицы, а их оценки. Нас будет интересовать на сколько “хорошо” со статистической точки зрения выборочные характеристики описывают соответствующие параметры для генеральной совокупности.
Доверительный интервал для i-го собственного числа ищется по формуле: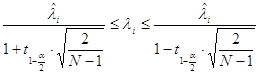
Доверительные интервалы для собственных чисел в итоге принимают вид:
![]()
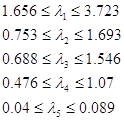
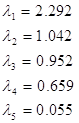
Оценка значения нескольких собственных чисел попадает в доверительный интервал других собственных чисел. Необходимо проверить гипотезу о кратности собственных чисел.
Проверка кратности производится с помощью статистики
![]() , где r-количество кратных корней.
, где r-количество кратных корней.
Данная статистика в случае справедливости ![]() распределена по закону
распределена по закону ![]() с числом степеней свободы
с числом степеней свободы ![]() . Выдвинем гипотезы:
. Выдвинем гипотезы:![]()
![]()
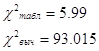
Так как ![]() , то гипотеза
, то гипотеза ![]() отвергается, то есть собственные числа
отвергается, то есть собственные числа ![]() и
и ![]() не кратны.
не кратны.
Далее,
:![]()
![]()
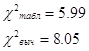
Так как ![]() , то гипотеза
, то гипотеза ![]() отвергается, то есть собственные числа
отвергается, то есть собственные числа ![]() и
и ![]() не кратны.
не кратны.
:![]()
![]()
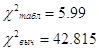
Так как ![]() , то гипотеза
, то гипотеза ![]() отвергается, то есть собственные числа
отвергается, то есть собственные числа ![]() и
и ![]() не кратны.
не кратны.
Необходимо выделить главные компоненты на уровне информативности 0,85. Мера информативности показывает какую часть или какую долю дисперсии исходных признаков составляют k-первых главных компонент. Мерой информативности будем называть величину: ![]()
I1=![]() =0,458
=0,458
I2=![]() =0,667
=0,667
I3=![]()
На заданном уровне информативности выделено три главных компоненты.
Запишем матрицу ![]() =
=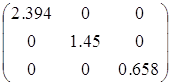
Для получения нормализованного вектора перехода от исходных признаков к главным компонентам необходимо решить систему уравнений: ![]() , где
, где ![]() - соответствующее собственное число. После получения решения системы необходимо затем нормировать полученный вектор.
- соответствующее собственное число. После получения решения системы необходимо затем нормировать полученный вектор.
Для решения данной задачи воспользуемся функцией eigenvec системы MathCAD, которая возвращает нормированный вектор для соответствующего собственного числа.
В нашем случае первых четырех главных компонент достаточно для достижения заданного уровня информативности, поэтому матрица U (матрица перехода от исходного базиса к базису из собственных векторов)
Строим матрицу U, столбцами которой являются собственные вектора:
U=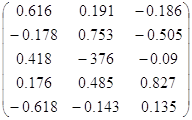 .
.
Матрица весовых коэффициентов:
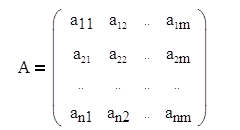
![]()
А=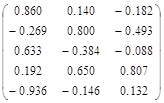 .
.
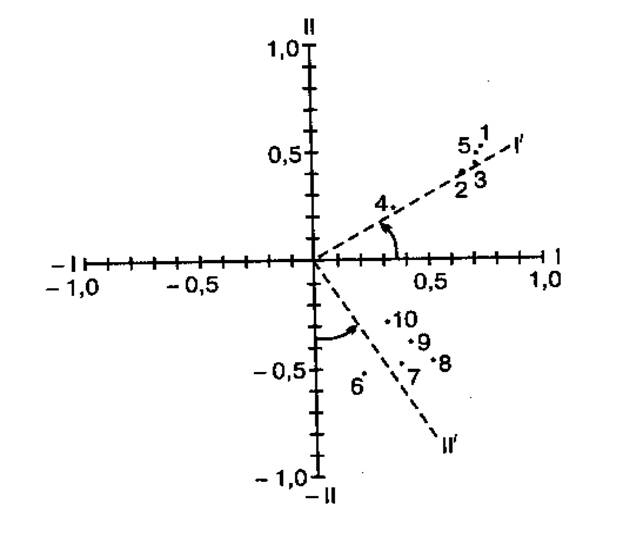
Коэффициенты матрицы А являются коэффициентами корреляции между центрировано – нормированными исходными признаками и ненормированными главными компонентами, и ![]() показывают наличие, силу и направление линейной связи между соответствующими исходными признаками и соответствующими главными компонентами.
показывают наличие, силу и направление линейной связи между соответствующими исходными признаками и соответствующими главными компонентами.
Похожие работы
... здесь можно довериться интуиции. В качестве предварительного варианта можно использовать имя переменной, которая вошла в фактор с наибольшей нагрузкой. 3.2. Разработка психодиагностического теста с применением факторного анализа на примере опросника “Шестнадцать личностных факторов (16PF)” Р.Кэттелла. Приложение факторного анализа к разработке личностных опросников в так называемой “лексической ...
... И ИНФОРМАТИКИ КАФЕДРА МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ И ЭКОНОМЕТРИКИ Контрольная работа по курсу: “Многомерные статистические методы” напо темуе: “КоррелЯционно-регрессионный, факторный и компонентный анализы деятельности предприятии”студента группы ЗС-301 шифр 96005 Башиной Екатерины Сергеевны Москва 1998 год СОДЕРЖАНИЕ Экономическая постановка задачи ...
... одного работника в % к заработной плате и меньше всего зависит от удельного веса потерь от брака и от удельного веса рабочих в составе промышленно-производственного персонала. Потом провели анализ с помощью линейной регрессии. Приведем протокол множественной линейной регрессии. *** Протокол множественной линейной регрессии *** Зависимая переменная Y - y2 Функция Y = -12.728+12.035*x4+28.237 ...
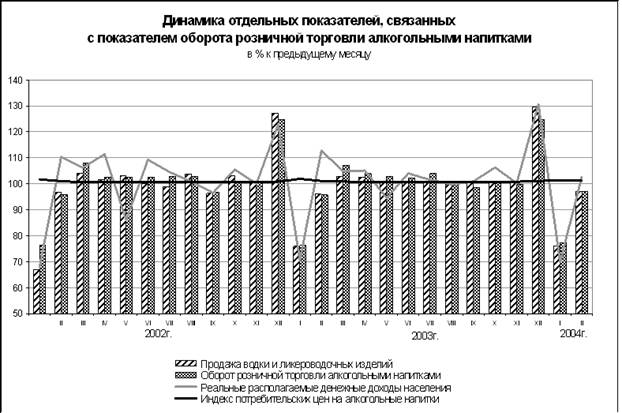
... сказалось несоответствие поставки (по ассортиментному составу или качеству) спросу населения Недопоставка также приводит к невыполнению плана розничного товарооборота. Анализ динамики товарооборота розничной торговли. Рассмотрим анализ розничного товарооборота в динамическом аспекте с помощью индексного метода. Для индексного метода характерным является сопоставление двух периодов—отчетного ...
0 комментариев