Графическая классификация предприятий по двум общим факторам

3.2 Графическая классификация предприятий по двум общим факторам

Чтобы графически произвести классификацию объектов, необходимо найти наблюденные значения первых двух общих факторов. Это можно сделать по формуле: , где

- транспонированная матрица факторных нагрузок;

- диагональная матрица, на главной диагонали которой стоят харак терности соответствующих общих факторов;

- матрица центрированно-нормированных значений исходных признаков.

Матрица наблюденных значений общих факторов приведена в Приложениях.

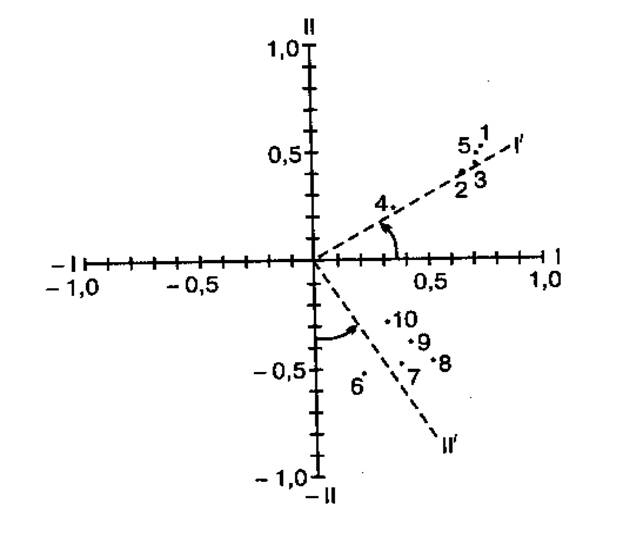
Отобразим объекты наблюдения в пространстве первых двух общих факторов.

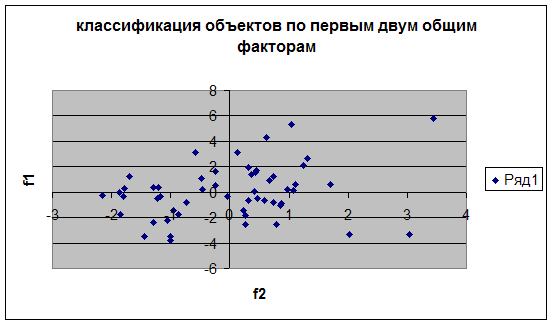
3.3 Переход к обобщенным факторам с помощью варимаксного вращения

В факторном анализе при решении практических задач широко применяется ортогональное вращение. Конечной целью факторного анализа является получение содержательно интерпретируемых факторов, которые воспроизводили бы выборочную корреляционную матрицу между переменными. Например, в методе главных факторов это достигается путем вращения.

Поскольку из множества положений системы координат надо выбрать одну, нужен критерий, который давал бы возможность судить о том, что мы близко подошли к своей цели. Таких критериев предложено много. Остановимся на наиболее часто используемом методе варимаксного вращения. Метод Варимакс рассчитывает V_j критерий качества структуры каждого фактора:

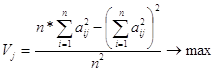
При помощи метода «варимакс» достигают максимального упрощения в описании столбцов матрицы факторного отображения. Возможно раздельноеулучшение структуры факторов. Наилучшим будет максимальное значение критерия. Если после очередного вращения V_j растет – переходим к вращению. Рассчитаем V_j для имеющейся матрицы А:V₁=0.307, V₂=0.168

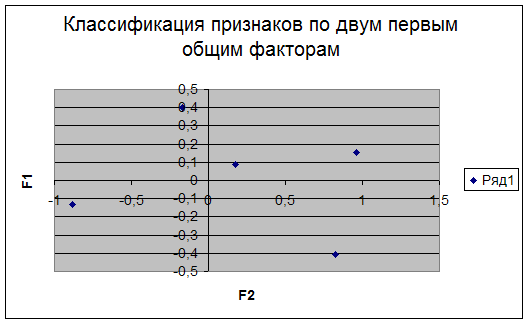
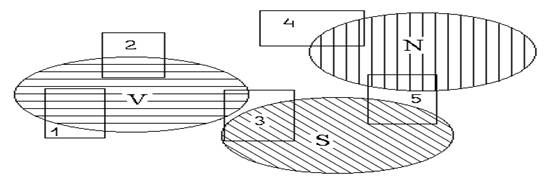
Рис.3: Классификация признаков.

Наша цель не только снизить размерность признакового пространства, но и предать выделенным факторам какой-то экономический смысл. Мы можем перейти с помощью вращения от факторов f1 и f2 к факторам f1 и f2 с помощью соотношения В=Т*А. Исходя из геометрических соображений, повернем систему координат по часовой стрелки на угол равный 15. Матрица вращения будет иметь вид:

Т=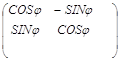

Известно, что sin15=0.259 cos15=0.966. Найдем матрицу В=Т*А

*=

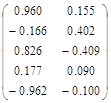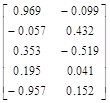
Рассчитаем V_j для матрицы В , полученной после вращения: V₁=0,240, V_j=0,156. Значение V_j не возросло ни по одному из факторов.

Попытки производить вращения на другие углы не приводят к возрастанию значения V_j следовательно нет необходимости во вращении.

3.4 Построение функции регрессии на выделенные обобщенные факторы

Используя данные о «наблюденных» значениях общих факторов, построим функцию регрессии на выделенные обобщенные факторы с помощью программы «Stadia».Получим уравнение регрессии следующего вида для i-го объекта наблюдения:

Подробное описание уравнения регрессии дано в Приложениях

Список использованных источников

1 Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы: Учебник. – М.: Финансы и статистика,1998.- 352с.

2 Сошникова Л.А., Тамашевич В.Н., Уебе Г., Шефер М. Многомерный статистический анализ в экономике: Учебное пособие для вузов- М.:ЮНИТИ-ДАНА, 1999.-598 с.

Приложение 1 Наблюденные значения исходных признаков

Y1	X5	X6	X7	X9	X17
9,26	0,78	0,4	1,37	0,23	17,72
9,38	0,75	0,26	1,49	0,39	18,39
12,11	0,68	0,4	1,44	0,43	26,46
10,81	0,7	0,5	1,42	0,18	22,37
9,35	0,62	0,4	1,35	0,15	28,13
9,87	0,76	0,19	1,39	0,34	17,55
9,17	0,73	0,25	1,16	0,38	21,92
9,12	0,71	0,44	1,27	0,09	19,52
5,88	0,69	0,17	1,16	0,14	23,99
6,3	0,73	0,39	1,25	0,21	21,76
6,22	0,68	0,33	1,13	0,42	25,68
5,49	0,74	0,25	1,1	0,05	18,13
6,5	0,66	0,32	1,15	0,29	25,74
6,61	0,72	0,02	1,23	0,48	21,21
4,32	0,68	0,06	1,39	0,41	22,97
7,37	0,77	0,15	1,38	0,62	16,38
7,02	0,78	0,08	1,35	0,56	13,21
8,25	0,78	0,2	1,42	1,76	14,48
8,15	0,81	0,2	1,37	1,31	13,38
8,72	0,79	0,3	1,41	0,45	13,69
6,64	0,77	0,24	1,35	0,5	16,66
8,1	0,78	0,1	1,48	0,77	15,06
5,52	0,72	0,11	1,24	1,2	20,09
9,37	0,79	0,47	1,4	0,21	15,98
13,17	0,77	0,53	1,45	0,25	18,27
6,67	0,8	0,34	1,4	0,15	14,42
5,68	0,71	0,2	1,28	0,66	22,76
5,22	0,79	0,24	1,33	0,74	15,41
10,02	0,76	0,54	1,22	0,32	19,35
8,16	0,78	0,4	1,28	0,89	16,83
3,78	0,62	0,2	1,47	0,23	30,53
6,48	0,75	0,64	1,27	0,32	17,98
10,44	0,71	0,42	1,51	0,54	22,09
7,65	0,74	0,27	1,46	0,75	18,29
8,77	0,65	0,37	1,27	0,16	26,05
7	0,66	0,38	1,43	0,24	26,2
11,06	0,84	0,35	1,5	0,59	17,26
9,02	0,74	0,42	1,35	0,56	18,83
13,28	0,75	0,32	1,41	0,63	19,7
9,27	0,75	0,33	1,47	1,1	16,87
6,7	0,79	0,29	1,35	0,39	14,63
6,69	0,72	0,3	1,4	0,73	22,17
9,42	0,7	0,56	1,2	0,28	22,62
7,24	0,66	0,42	1,15	0,1	26,44
5,39	0,69	0,26	1,09	0,68	22,26
5,61	0,71	0,16	1,26	0,87	19,13
5,59	0,73	0,45	1,36	0,49	18,28
6,57	0,65	0,31	1,15	0,16	28,23
6,54	0,82	0,08	1,87	0,85	12,39
4,23	0,8	0,68	1,17	0,13	11,64
5,22	0,83	0,03	1,61	0,49	8,62
18	0,7	0,02	1,34	0,09	20,1
11,03	0,74	0,22	1,22	0,79	19,41

№	f1	f2	f3
1	0.465	0.513	-0.722
2	0.521	-0.576	-0.18
3	-0.918	-0.263	-0.119
4	-0.53	0.434	-0.672
5	-1.703	-0.315	0.16
6	0.527	-0.593	0.05
7	-0.574	0.059	0.243
8	-0.455	0.651	-0.508
9	-1.005	-0.546	0.676
10	-0.495	0.48	-0.315
11	-1.401	0.233	0.292
12	-0.293	0.333	0.082
13	-1.516	0.049	0.366
14	-0.277	-1.222	0.996
15	-0.456	-1.647	0.942
16	0.722	-0.662	0.164
17	1.067	-0.793	0.279
18	1.029	-0.334	0.062
19	1.246	-0.106	-0.118
20	1.05	0.109	-0.534
21	0.569	-0.175	-0.127
22	1.149	-1.072	0.215
23	-0.212	-0.722	0.771
24	0.698	0.853	-1.066
25	0.399	0.874	-1.153
26	1.007	0.311	-0.723
27	-0.523	-0.562	0.473
28	0.797	6.03E-3	-0.184
29	-0.225	1.458	-0.957
30	0.382	0.833	-0.584
31	-1.525	-1.642	0.833
32	-0.161	1.809	-1.328
33	-0.185	-0.104	-0.45
34	0.395	-0.45	-0.103
35	-1.426	-0.081	0.145
36	-1.057	-0.412	-0.012
37	1.263	0.194	-0.811
38	0.016	0.516	-0.546
39	0.211	-0.1	-0.251
40	0.576	-0.082	-0.332
41	1.703	3.644	5.731
42	-0.235	-0.339	0.019
43	-1.023	1.293	-0.705
44	-1.656	0.487	0.022
45	-1.047	0.164	0.457
46	-0.211	-0.573	0.546
47	-0.017	0.608	-0.645
48	-1.804	-0.119	0.487
49	2.464	-1.953	-0.182
50	0.543	2.607	-1.793
51	2.391	-1.4	-0.05
52	-0.127	-1.581	0.901
53	-0.131	-0.094	0.26

Приложение 2

Главные компоненты                           Приложение 3 Построение уравнения регрессии на главные компоненты.

ПОШАГОВАЯ РЕГРЕССИЯ. Файл: гл.комп.std

Пропущн=2 2

Переменная Среднее Ст.отклон.

f1 3,77E-5 1

f2 5,66E-7 1

f3 3,77E-5 1

Y 7,97 2,61

Корреляционная матрица

f1 f2 f3 Y

f2 0

f3 -0,001 0

Y 0,044 0,009 -0,167

 

 Критичeское значение=0,57

 Число значимых коэффициентов=0 (0%)

*** Метод включения. Шаг No.1, введена переменная:f3

Коэфф. a0 a1

Значение 7,97 -0,437

Ст.ошиб. 0,357 0,36

 Значим. 0 0,229

Источник Сум.квадр. Степ.св Средн.квадр.

Регресс. 9,92 1 9,92

Остаточн 344 51 6,75

Вся 354 52

Множеств R R^2 R^2прив Ст.ошиб. F Значим

0,16732 0,0279970,0089386 2,5985 1,47 0,144

Гипотеза 0: <Регрессионная модель неадекватна экспериментальным данным>

Измен.R^2 F Значим

0,028 1,47 0,229

-------------- Переменные в уравнении ---------------

 Переменн. Коэфф.В Ст.ош.В Бета F Значим

f3  -0,437 0,36 -0,167 1,47 0,229

------------------ Переменные не в уравнении ---------------------------

 Переменн. Коэфф.В Ст.ош.В Бета F Значим Частн.R Толер.

f2 0,0241 0,364 0,00922 0,00438 0,946 0,00935 1

f1 0,116 0,364 0,0446 0,102 0,749 0,0452 1

 

Приложение 4

«Наблюденные» значения общих факторов.

№	f1	f2	f3
1	0.745	янв.23	1.313
2	0.734	-0.836	0.704
3	-0.238	0.527	0.758
4	0.318	1.969	1.578
5	-1.211	0.409	0.318
6	0.232	-1.468	0.097
7	-1.22	-0.515	-0.57
8	-0.25	1.614	0.959
9	-1.849	-1.743	-1.129
10	-0.476	01.апр	0.564
11	-1.789	0.264	-0.56
12	-1.179	-0.298	-0.439
13	-1.87	0.016	-0.572
14	-1.44	-3.51	-1.681
15	-1.009	-3.509	-1.145
16	0.266	-1.837	-0.201
17	0.259	-2.529	-0.505
18	0.857	-1.027	-0.204
19	0.878	-0.868	-6.854E-3
20	1.076	0.101	0.966
21	0.307	-0.685	0.247
22	0.791	-2.553	-0.15
23	-1.051	-2.264	-1.434
24	1.241	2.131	1.901
25	1.312	2.653	2.214
26	1.117	0.583	1.302
27	-0.957	-1.415	-0.703
28	0.459	-0.507	0.197
29	0.122	3.157	1.449
30	0.437	1.527	0.772
31	-1.286	-2.376	-0.534
32	0.618	апр.32	2.167
33	0.666	0.896	1.303
34	0.582	-0.631	0.472
35	-1.295	0.351	0.086
36	-0.463	0.212	0.634
37	1.705	0.623	1.523
38	0.366	1.402	1.025
39	0.423	0.057	0.635
40	0.965	0.228	0.766
41	3.449	май.79	-16.471
42	-0.049	-0.334	0.249
43	-0.578	мар.14	1.174
44	-1.702	1.212	0.04
45	-1.802	-0.354	-1.028
46	-0.864	-1.729	-0.953
47	0.449	1.732	1.235
48	-2.152	-0.24	-0.695
49	3.036	-3.314	1.159
50	1.037	5.343	2.573
51	2.026	-3.347	0.406
52	-1.012	-3.805	-1.202
53	-0.731	-0.83	-0.606

 

Приложение 5

Уравнение регрессии на общие факторы.

МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ.

 

Коэфф. a0 a1 a2 a3

Значение 7,97 0,309 0,0722 0,186

Ст.ошиб. 0,359 0,309 0,177 0,145

 Значим. 0 0,323 0,688 0,204

Источник Сум.квадр. Степ.св Средн.квадр.

Регресс. 19,3 3 6,43

Остаточн 335 49 6,84

Вся 354 52

Множеств R R^2 R^2прив Ст.ошиб. F Значим

0,2333 0,054428-0,0034647 2,6147 0,94 0,57

Гипотеза 0: <Регрессионная модель неадекватна экспериментальным данным>