Навигация
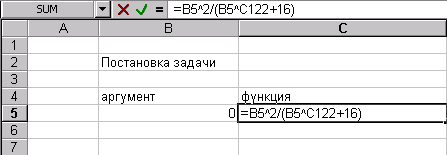
2.2. В поле Значение ввс
В нашем случае это значение равно О.
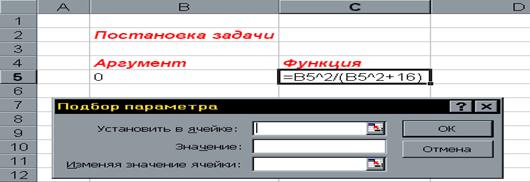
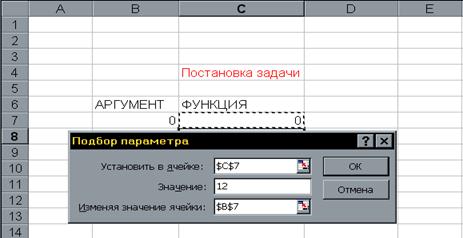
2.3 В поле, Изменяя значение ячейки ввести адрес клетки, где задано начальное приближение решения, в нашем случае это клетка В 5 (абсолютный адрес которой $В$5 появится в поле после щелчка левой клавиши мыши на клетке В5).После выполнения пунктов 1-2 страница электронной таблицы будет выглядеть так, как показано на Рис.3.
Правая часть решаемого уравнения не обязана быть всегда нулем равнение (2) преобразовать к виду 10*х*(х+10)/(х-9)=2. то в поле Значение следовало бы установить 2.
После нажатия на кнопке ОК появится окно Результат подбора параметра, в котором дается о том нацдена ли решение, чему равна и какова точность полученного решения.
Для нашего примера Результат подбора параметра показан на Рис.4
При значении аргумента –0,187204141 функция, стоящая в левой части уравнения (2) отличается от нуля на – 0,000484158.
Достигнутая точность решения равна – 1.0Е-3
Если полученные значения следует "отразить на листе электронной таблицы, то надо щелкнуть на кнопке ОК . .если же нет то на кнопку Отмена. В первом случае найденные значения зафиксируются в клетках В5 и С5 и лист электронной таблицы будет выглядеть как на Рис.5, или как на Рис.6, если установить режим отображения результатов, предварительно сняв режим отображения формул, выполнив команду Сервис/Параметры/Вид/Формулы.
Численные методы решения уравнений хороши тем, что мoжно получить приближенное решение с заданной точностью. EXCEL име (возможность управлять выбором точности. Для этого надо выполни' команду Сервис/Параметры/Вычисления и в соответствующих полз установить. значения относительной погрешности и количества итераш Рис.7
1.2 Системы двух линейныхалгебраических уравненийВышеизложенный способ получения решения уравнения может быть легко распрастранен для случая решения ситемы двух уравнений с двумя неизвестными, если ситема имеет следующий вид.
Y=Ф (х)
Y=y(х)
В каждом уравнении системы функции у явна выражена через х
Преобразуем систему (3) в одно уравнение вида (+)
Ф (х) -'^(х) = 0 - (4)
Полученное уравнение уже можно решить с помощью Подбора параметра... так как это было описано выше.
В качестве примера рассмотрим нахождение равновесных цены и объема продаж для рынка некоторого товара.
Пусть функция спроса на товар имеет вид Q = 40/(Р+3) а функция предложения: Q = 20Р-14
Найти равновесные цену и объем , построить графики спроса и предложения.
Имеющуюся систему уравнений Q=40/(p+3)
Q=20Р-14
преобразуем в одно уравнение вида 40 / (р + 3) - 20 р +14=0
Подбором параметра... описанным выше, находим равновесную цену, она равна 1,17, подставив это значение в одно из уравнений системы, получим и значение равновесного объема - 9,57. Для построения графика, иллюстрирующего ситуацию равновесия спроса и предложения на рынке, воспользуемся знанием равновесной цены и возьмем значения цен в некоторой окрестности от нее. например от 0 до 4 с шагом 0,1.
Используя все возможности мастера диаграмм, получим следующую иллюстрацию решения задачи о равновесии на рынке. Рис.8.
Задание1Найти ближайшее к начальному приближению решение следующих уравнений. Исследовать влияние начального приближения на найденное решение
10x-x+56=12
Задание 2
Подбором параметра... найти точку равновесия рынка некоторого товара, для чего решить систему уравнений, описывающих спрос и предложение этого товара. Построить и оформить график равновесия.
Функция спроса
Q=50e-3
Функция предложения
Q=3p-4e
0<p<20
Глава 2. Матричная алгебраПо мнению крупнейшего экономиста нашей эпохи В.В.Леонтьева. «Дифференциальное исчисление и элементарная алгебра - два традиционных инструмента экономиста-математика заменяются . или, по крайней мере дополняются матричной алгеброй.»4Матричная алгебра тесно связана с линейными функциями и с линейными ограничениями в связи с чем находит себе применение в различных экономических задачах:
• в эконометрике, для оценки параметров множественных линейных регрессий;
• при решении задач линейного программирования;
• при макроэкономическом моделировании и т.д. Особое отношение к матричной алгебре в экономике появилось после создания моделей типа «Затраты - Выпуск», где с помощью матриц технологических коэффициентов объясняется уровень производства в каждой отрасли через связь с соответствующими уровнями во всех прочих отраслях.
Электронная таблица EXCEL имеет ряд встроенных функций для работы с матрицами:
ТРАНСП - транспонирование исходной матрицы - вычисление определителя квадратной матрицы
МОПРЕД- вычисление определителя квадратной матрицы
МОБР - вычисление матрицы обратной к данной - нахождение матрицы, являющейся произведением двух матриц.Кроме того возможно выполнение операций поэлементного сложения (вычитания ) двух матриц и умножения (деления) матрицы на число. Все вышеперечисленные функции вызываются через мастер функций и хотя относятся к разделу математических, они располагаются в полном алфавитном перечне.
МУМНОЖ- нахождение матрицы, являющейся произведением двух матриц.
Кроме того возможно выполнение операций поэлементного сложения (вычитания ) двух матриц и умножения (деления) матрицы на число.
Все вышеперечисленные функции вызываются через мастер функций и хотя относятся к разделу математических , они располагаются в полном алфавитном перечне.
2.1 Определитель матрицыДля вычисления определителя матрицы сформируем лист электронной таблицы, как показано на Рис.9. Место записи вычисленного определителя матрицы определяется местоположением табличного курсора.
Пусть на листе электронной таблицы сделаны все предварительные действия, т.е введена матрица, над которой будут производиться действия и определено место записи результата.
Следующим шагом вызывается мастер функций рис10., левое окно которого содержит перечень разделов , а правое алфавитный список функций, составляющих данный раздел.
В левом окне выбираем раздел -« Полный алфавитный перечень «, а в правом МОПРЕД , В появившемся диалогом окне Рис11. Следует указать левый верхний и через двоеточие правый нижний адреса матрицы, (или обвести интересующую нас матрицу, при нажатой клавиши мыши, штриховой линией, что автоматизирует процесс определения адресов местоположения матрицы на листе ЭТ) Рис.11
Щелкнув на кнопке Готово получим значение определителя, размещенного в клетке С10. Его значение равно 1 Нахождение определителя - это единственное действие .над матрицей, которое дает в результате число, остальные матричные функции в результате своих действий дают матрицы и , это,следует, учитывать при подготовке на листе ЭТ места для размещения результата.
2.2 Умножение матрицВ качестве примера рассмотрим умножение двух матриц. Пусть надо умножить матрицу А(5*4) на матрицу В(4*3). это умножение возможно, так как число столбцов матрицы А совпадает с числом строк матрицы В . результатом будет матрица С(5*3).
Перед вызовом функции умножения матриц сформируем лист ЭТ, так как показано на Рис.12
Затем выполним следующую последовательность действий:
1.Зададим матрицу А
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... 7”. Режим значений — “Приложение 8”. 1.2). Проверка — сравнение результатов, полученных разными способами. Для наглядности создадим сравнительную таблицу: Математический расчет методом обратной матрицы Обращение матрицы в EXCEL x1 0,521737 0,521737318 x2 0,391105 0,391104998 x3 1,019069 1,019069651 1.3). Вывод. Сначала ...
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...
... на объем выручки оказывает также и используемые методы её определения и учета. 1.2Методы определения и учета выручки Выручка от реализации продукции (работ, услуг) может рассчитываться либо по мере отгрузки и предъявления заказчику расчетных документов либо по поступлению денежных средств на счета в коммерческих банках, а при расчетах наличными деньгами – по поступлению денежных средств в ...

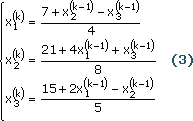
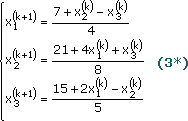



0 комментариев