Навигация
2. Зададим матрицу В
3 Отметим место для матрицы С7
4. Обратимся к мастеру функций , найдем в полном алфавитном перечне функцию МУМНОЖ и выполним постановку задачи так. Как показано на Рис. 13
В качестве массива 1 указывается диапазон адресов матрицы А, а в качестве массива 2- диапаон адресов матрицы В.
Щелкнуть в на кнопке Готово получим в клетке, где присутствует знак равенства, полную запись функции умножения. Для получения результата необходимо нажать клавиши Shift/Ctrl/Enter одновременно8
7В выделенном под результат месте ЭТ поставить знак равенства.
8Все матричные функции, за исключением вычисления определителя. требуют заключительного одновременного нажатия клавиш Shift/Ctrl/Enter
На Рис 15 показан результат умножения после нажатия клавш Shift/Ctrl/Enter, а в строке формул стоит выражение в "фигурны скобках, {3*B4:D6} что является признаком выполнения матрично операции
Сложение матриц
Для сложения двух матриц одинаковой размерности10 следует выполнить следующую последовательность действий. . Задать две исходных матрицы. . Отметить место для матрицы - результата. • . В выделенном под результат месте ЭТ поставить знак равенства и записать сумму так. как показано на Рис. 16. . -Завершить выполнение работы нажатием клавиш Shift/Ctrl/Enter, Рис.17".
Фигурные скобки в строке формул {В4:D6+F4:H6}-признак выполнения матричной операции
Задание 3
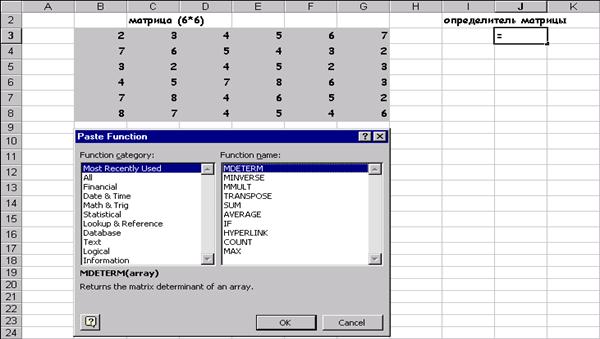
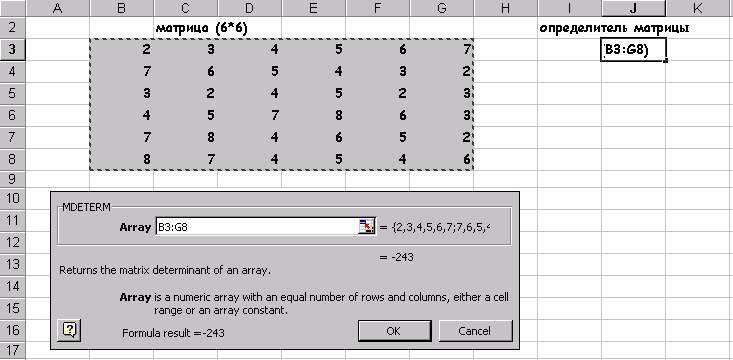
Найти определитель матрицы В (6*6):. умножить матрицу на 14.
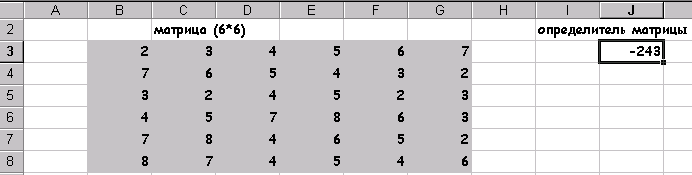
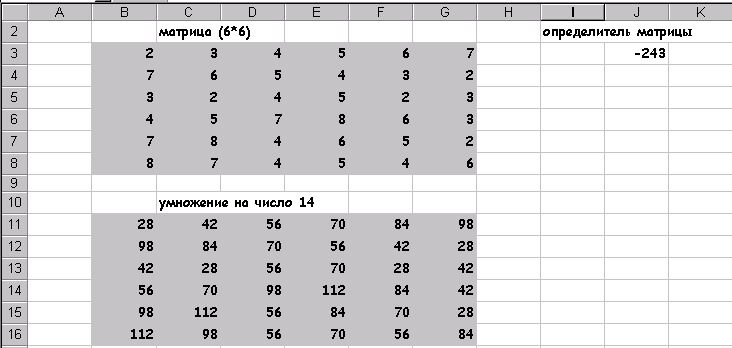
Умножение на число 14

результат:
Задание 4
Транспонирование матрицы А :
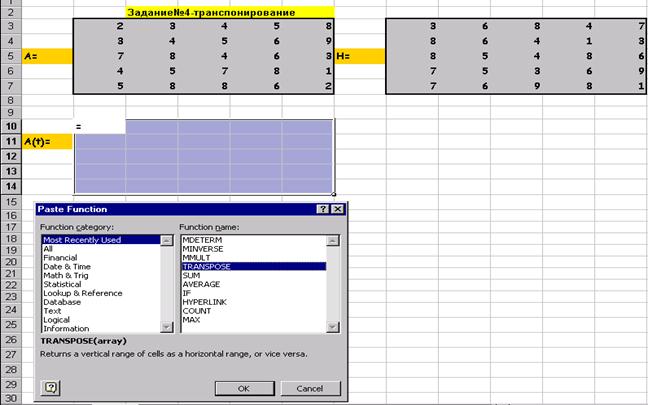
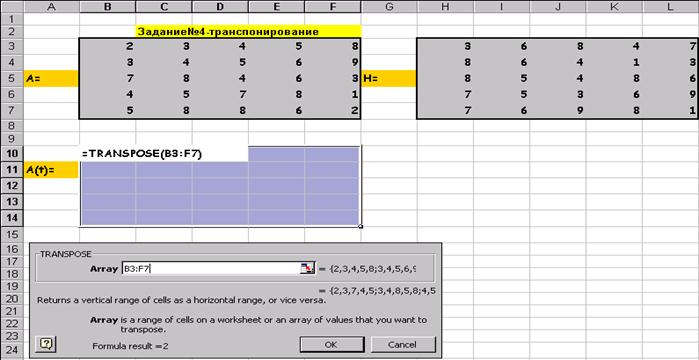
После нажатия Shift/Ctrl/Alt:
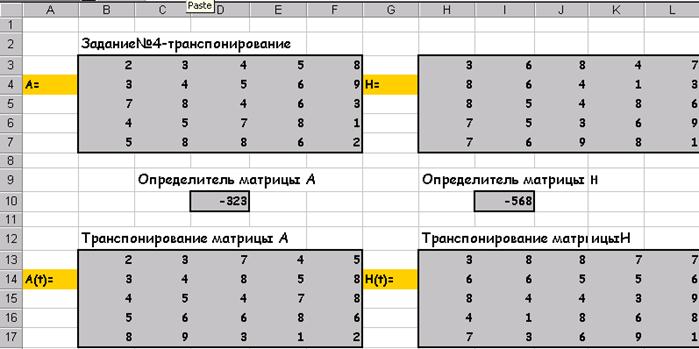
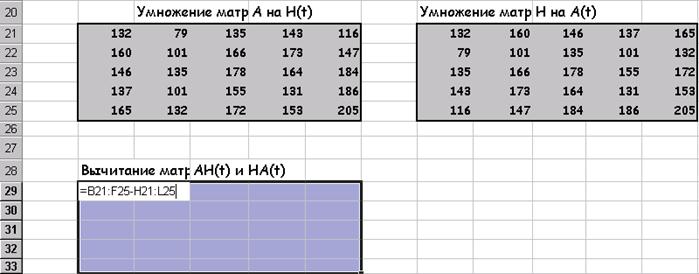
Умножение матриц А на H(t):
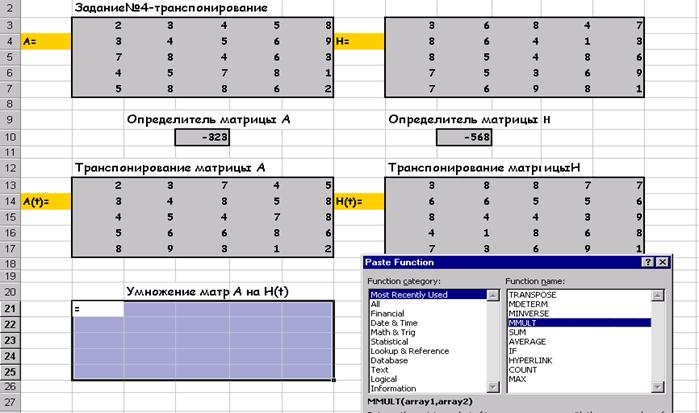
После нажатия на ОК:

Вычитание матриц AH(t) и HA(t):

2.6 Система линейных алгебраических уравнений
Решение Система линейных алгебраических уравнений всегда занимало математиков и для решения было разработано немало численных методов, подразделяющихся на прямые ( Гаусса, Кремера) и итерационные (простых итераций , Зейделя ,верхних релакций… )
EXCEL задача получения решение СЛАУ решаются с помощью вышеописанных матричных функций, для чего исходную систему надо представить в виде матричного уравнения.
Рассмотрим последовательность действий для получения решение СЛАУ на конкретном примере.
Задание 5Найти решение системы линейных алгебраических уравнение и сделать проверку.



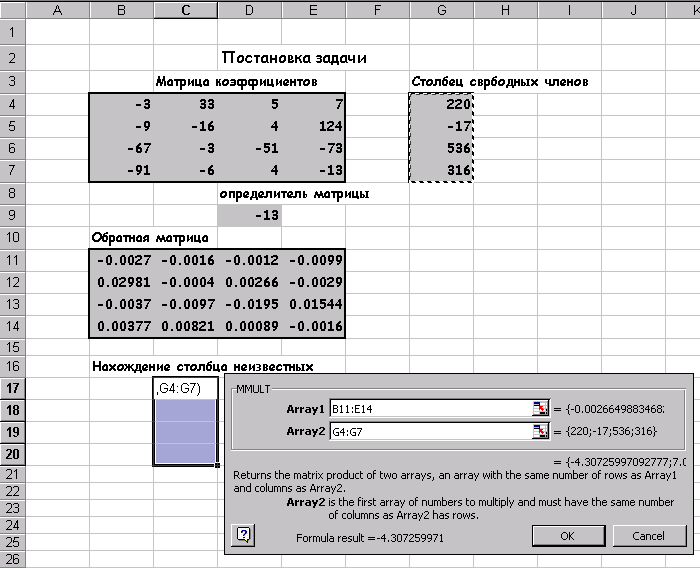
Для того, чтобы система (5) имела единственное решение необходимо и достаточно, чтобы определить системы, составленный из коэффициентов при переменных х,х,х,х, не был равен нулю.
Рассчитаем определить системы пользуясь функцией МОПРЕД. Рассчитанное значение определителя системы равно 1662723продолжать процесс поиска решения.
Из линейной алгебры известна матричная запись системы уравнений и матричное преставление решения.
Перепишем систему уравнений (5):
Тогда матричное решение уравнения выглядит так:
Результат, указанный на рис18 можно получить, выполнив следующие действия:
1. Вычислить определитель и выяснить имеет ли система единственное решение.
2. Вычислить матрицу обратную к исходной.
3. Найти произведение обратной матрицы и вектор столбца свободных членов.
Глава3. Поиск решения… 1.2Оптимизация
Почти любую ситуацию , встречающуюся в деловой личной общественной жизни можно охарактеризовать как ситуацию принятия решения. Для задач принятия решений существенными являются следующие общие элементы:
1. Множества переменных и параметров. В их число входят:
Множество разрешающих или эндогенных переменных, значения которых рассчитываются лицом, принимающим решение.
Множество внешних или экзогенных переменных, значения которых не контролируются лицом, принимающим решение.
Множество параметров, которые так же контролируется и считаются в условиях задачи вполне определенными.
Модель-множество соотношений, связывающих все переменные и параметры.
Целевая функция-функция, функций, значение которой зависит от значений эндогенных переменных. Эта функция. Позволяет лицу, принимающему решения оценивать варианты.
Численные методы-методы, с помощью, которых можно систематически оценивать результаты различных решений.
Получение решения на модели, в конечном итоге, сводится к математической задаче нахождения некоторых вещественных значений эндогенных переменных, которые оптимизируют целевую функцию.
Если до недавнего времени все четыре перечисленные выше элемента ложились на лицо принимающее решение, то теперь умение пользоваться встроенными функциями EXCEL снимает наиболее утомительный пункт, а именно, применения численных методов, и делает исследование задач принятия решения более эффективными, так как теперь для решения одной и той же более эффективными, так как теперь для решения одной и той же задачи можно быстро просмотреть различного вида постановки в том числе и отличающиеся друг от друга по структуре.
3.2Безусловный экстремум
Excel обладает мощным встроенным средством для нахождения экстремальных значений функции одной или нескольких переменных. Для одно-экстремальных функций можно найти безусловный глобальный экстремум. Для многоэкстремальных функций можно найти условный локальный экстремум. Забегая вперед отметим, что для многоэкстремальных функций определить какой из локальных экстремумов будет найден невозможно без построения графика функции на интересующем нас интервале, так как численные методы нахождения экстремума ориентированы на поиск ближайшего решения к точке начального приближения и вообще говоря, требуют унимодальности функции.
Посмотрим различные примеры поиска экстремальных значений функции.
Задание6Найти минимум и максимум функции на интервале, построить график.
2. ![]()

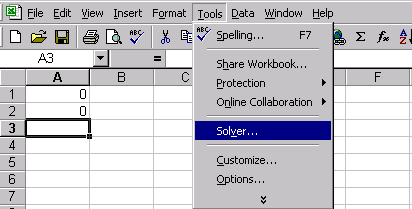

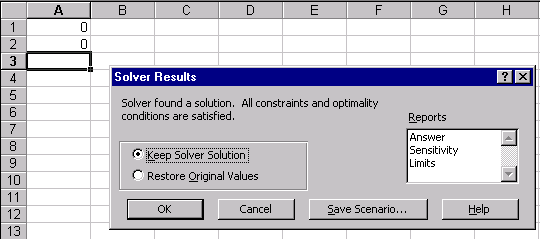
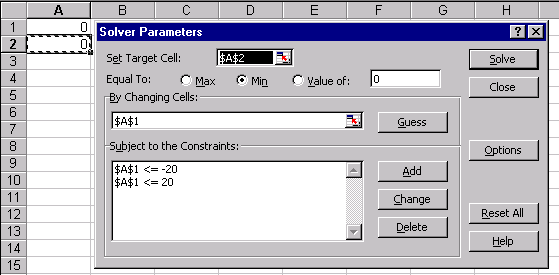
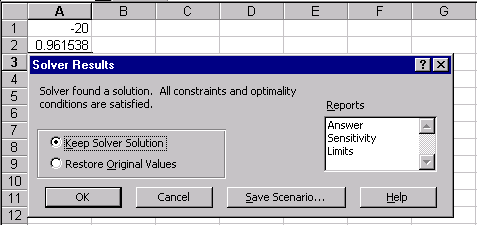
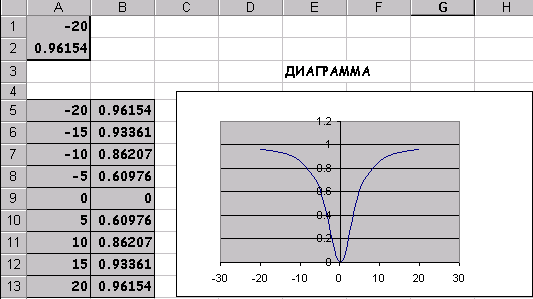
Рис.19
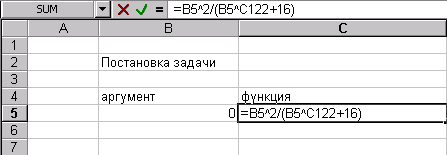
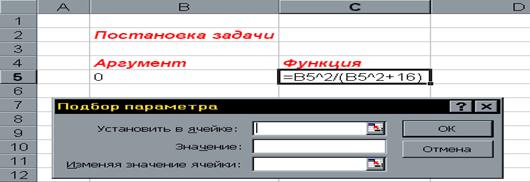
Для поиска безусловного экстремума функции сформируем лист электронной таблицы, как показано на рисунке 20. Функцию (6) запишем в клетку А2 где вместо переменной х следует указать адрес ячейки А1, которая содержит начальное приближение экстремума равное, например 0.
Для поиска минимума следует выполнить следующую последовательность действий:
1.Выполнить команду Сервис/Поиск решения…(получим лист электронной таблицы, как показано на рис.20).
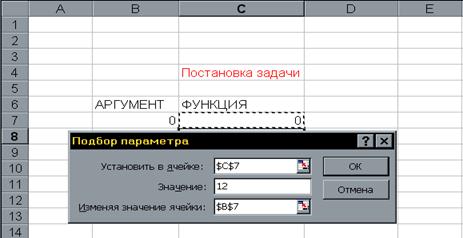
2.Заполнить диалоговое окно Поиск решения… рис21
2.1.Щелкнуть левой клавишей мыши в поле. Установить целевую ячейку и щелкнуть на ячейке с формулой, в нашем случае это ячейка А2, абсолютный адрес которой. $А$2 появится в поле.
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... 7”. Режим значений — “Приложение 8”. 1.2). Проверка — сравнение результатов, полученных разными способами. Для наглядности создадим сравнительную таблицу: Математический расчет методом обратной матрицы Обращение матрицы в EXCEL x1 0,521737 0,521737318 x2 0,391105 0,391104998 x3 1,019069 1,019069651 1.3). Вывод. Сначала ...
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...
... на объем выручки оказывает также и используемые методы её определения и учета. 1.2Методы определения и учета выручки Выручка от реализации продукции (работ, услуг) может рассчитываться либо по мере отгрузки и предъявления заказчику расчетных документов либо по поступлению денежных средств на счета в коммерческих банках, а при расчетах наличными деньгами – по поступлению денежных средств в ...

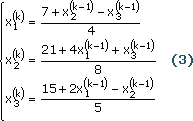
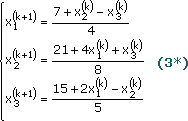



0 комментариев