Навигация
Выбрать поле Минимальное значение
2.2. Выбрать поле Минимальное значение.
2.3. В поле. Изменяя ячейки ввести адреса ячеек, значения которых будут варьироваться в процессе поиска решения. В нашем случае это клеикаА1, абсолютный адрес которой. $А$1.
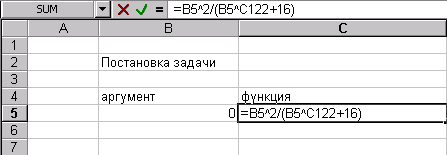
После выполнения пунктов 1-2 лист электронной таблицы будет выглядеть так, как показано на рис 21.
После щелчка на кнопке Выполнить получим решение поставленной задачи. В клетке А1 находится значение переменной Х равное 0.769231 при котором функция (5 ) достигает минимального значения равного –167,692. Рис22
Условный экстремум
Для функции одной переменной поиск экстремума возможен как на всей числовой оси, так и на некотором интервале, поиск на интервале уже можно считать поиском условного экстремума функции, т.к появляются ограничения на изменение значений аргумента.
На рис.21 в диалогом окне Поиск решения есть поле Ограничения м соответствующие ему команды: Добавить, Заменить, Удалить.
Рассмотрим предыдущую задачу, добавив условие поиска минимального значения на интервале [1;5]. Тогда диалоговое окно Поиск решения… следует видоизменить, добавив ограничения:
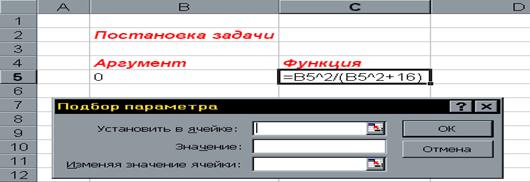
Щелкнув левой клавишей мыши в поле Ограничения и затем на кнопке Добавить , откроем диалоговое окно Добавление ограничения. Рис23,,,.. которое следует заполнить так как показано на рисунке.
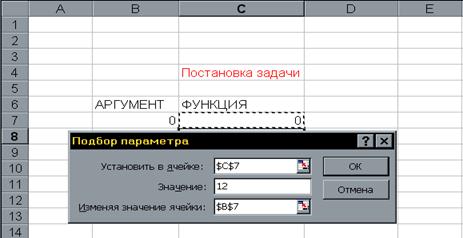
После добавления последнего ограничения диалоговое окно Поиск решения…будет содержать математическую постановку задачи экстремума и выглядит след.образом.
После щелчка на кнопке Выполнить получим следующее решение:
У=-167 при х=1, отличающееся от решения, полученного в предыдущем случае. Здесь в качестве минимального значения выступает наименьшее значение функции на интервале[1;5], совпадающее с левой границей интервала.
Все численные методы нахождения оптимальных значений для корректной работы требуют ,чтобы функция на интервале была унимодальной.
При такой постановке задачи значения труда и капитала определяется как 5 и 2 единицы соответственно. Получающиеся значение целевой функции при этом равно 3.37. Теперь можно построить график, на котором отражены линия безразличия использования труда и капитала при выпуске 3.37 и линия ограничения на средства, предназначенные для расходов на труд и капитал.
Полученные кривые касаются в найденной точке, что согласуется с теорией фирмы. Рис 31

3.4 Математическое программирование
Различные методы оптимального управления, получившие заметное развитие во второй половине двадцатого века, благодаря созданию и распространению компьютерной техники, не только отвечают насущным потребностям экономической науки, но и начинают играть роль важнейшего ее составного элемента. И это вполне естественно, поскольку одной из главных задач экономической науки является разработка теоретического фундамента управления, т.е. методов наилучшего распределения ограниченных ресурсов (людских, материально -вещественных, финансовых, временных) для поддержания функционирования и развития предприятия или экономики страны.
Однако, чтобы обнаружить глубинную связь между математическим программированием и экономической наукой, понадобились усилия многих ученых.
Анализируя возможности Поиска решения … можно заметить, что он применим для решения достаточно широкого класса задач математического программирования.
Если задачу принятия решений в области управления можно сформулировать в виде подчиненных m произвольным ограничениям.
![]() при
при
![]()
![]()
……………………
gm(x1,x2,…,xn)![]() 0
0
то Поиск решения… позволяет найти решение такой задачи, которая в формальной постановке может быть задачей:
1. линейного программирования
2. нелинейного программирования
3. целочисленного программирования
4. частично целочисленного программирования
Кроме того у лиц, принимающего решения есть возможность изменить параметры работы Поиска решения…, повышающие эффективность поиска оптимального решения. Рис.32
3.4.1. Линейное программирование
![]() Найти минимум функции F=5x1+x2
Найти минимум функции F=5x1+x2![]() min
min
![]() при ограничениях:
при ограничениях:
![]() 3x1+4x2
3x1+4x2![]() 12
12
![]() -2x1+x2
-2x1+x2![]()
![]() x1-2x2
x1-2x2![]()
![]() x1+x2
x1+x2![]() x1,x2 – произвольные
x1,x2 – произвольные
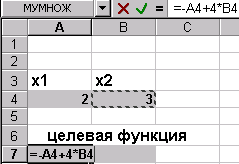
Сформируем страницу электронной таблицы и постановку задачи линейного программирования в диалоговом окне Поиска решения…
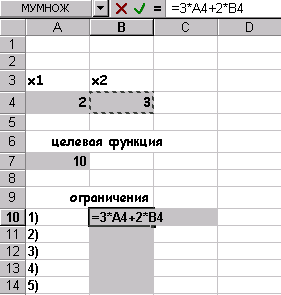
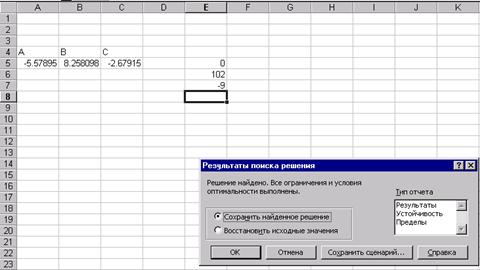
После выполнения поставленной задачи получаем следующее значение переменных
Как видим, при найденных значениях x1,x2 целевая функция принимает минимальное значение, равное –9.66 и этим удовлетворяются все ограничения поставленной задачи.
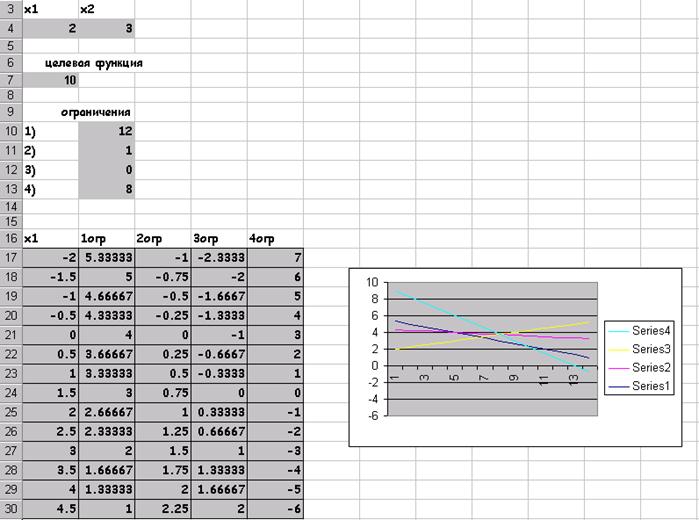
Графическое решение поставленной задачи выглядит так:
Задание 7
Решить задачу линейного программирования с помощью Поиска решения…, показать графически область допустимых решений и целевую функцию.
2.F=-x1+4x2![]()
при
3x1+2x2![]()
2x1-x2![]()
-3x1+2x2![]()
x1+2x2![]()
x1![]()
Задание 8
По описанию задачи сделать математическую постановку, решить.создать отчет и прокомментировать его.
№2
Фирма изготовляет два типа электрических выключателей, типа А, доход от которых равен 0.4$. На каждый выключатель и типа В – доход от которых равен 0.3$. На изготовление выключателя А требуется в три раза больше рабочего времени, чем на изготовления типа В.
Если бы изготавливались выключатели только типа В, то дневного рабочего времени хватило бы для изготовления ровно 1000 выключателей. Поставка медного провода обеспечивает изготовление только 800 выключателей в день (любого типа). Для выключателей требуются специальные изоляторы, их можно получить в день для типа А не более 400, для типа В не более 700. Задача состоит в максимизации дохода при всех указанных выше ограничениях.
Задание 9
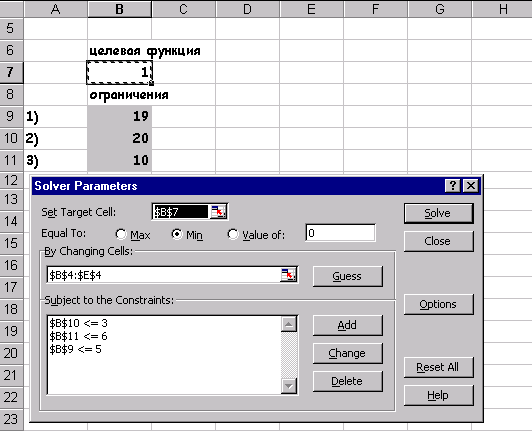
Составить задачу двойственную к данной задаче линейного программирования и решить обе с помощью Поиска решения…
2.F=-x1+x2![]()
при
x1+2x2 –x3 £5 ![]()
2x2+x4£3
x3+2x4£6
xj³0.j=1.4
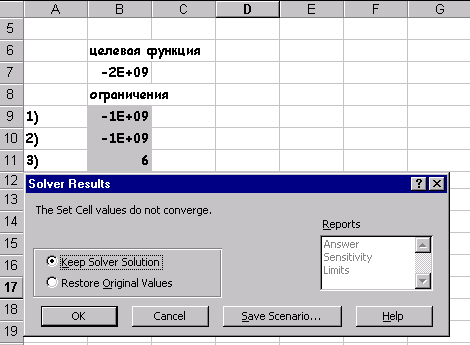
Задание 12
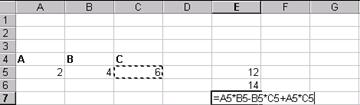
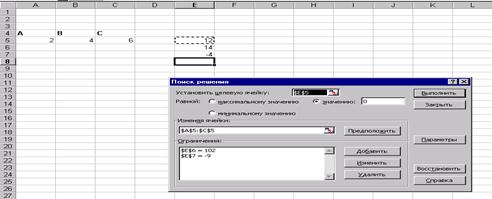
С помощью Поиска решения… найти решение системы нелинейных алгебраических уравнений. Исследовать зависимость получаемого решения от различных начальных приближений(менее трёх), оформить исследования в виде таблицы.
№2
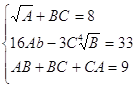
ЛИТЕРАТУРА:
1. EXCEL5.0 Для профессионалов. М-1995
2. EXCEL7.0 М-1997
3. А.А.Горчаков, И.В.Орлов. Компьютерные экономико-математические модели. М-1995
4. И.Л.Акулич. Математическое программирование а в примерах и задачах. М-1986
5. М.Кубонива. Математическая экономика на персональном компьютере. М-1991.
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... 7”. Режим значений — “Приложение 8”. 1.2). Проверка — сравнение результатов, полученных разными способами. Для наглядности создадим сравнительную таблицу: Математический расчет методом обратной матрицы Обращение матрицы в EXCEL x1 0,521737 0,521737318 x2 0,391105 0,391104998 x3 1,019069 1,019069651 1.3). Вывод. Сначала ...
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...
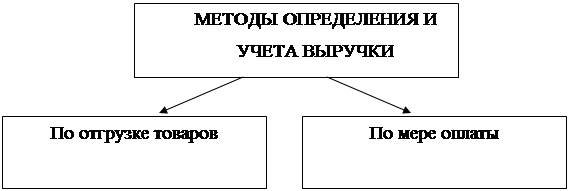
... на объем выручки оказывает также и используемые методы её определения и учета. 1.2Методы определения и учета выручки Выручка от реализации продукции (работ, услуг) может рассчитываться либо по мере отгрузки и предъявления заказчику расчетных документов либо по поступлению денежных средств на счета в коммерческих банках, а при расчетах наличными деньгами – по поступлению денежных средств в ...

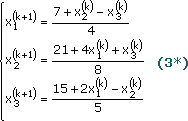



0 комментариев