Навигация
В ряде случаев, например при решении задач на многогранные углы
4. В ряде случаев, например при решении задач на многогранные углы,
вычисления упрощаются, если ввести единичные векторы, отложенные от вершины многогранного угла.
Примеры задач, решаемых векторным методом.
З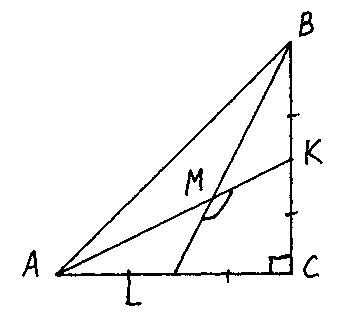 адача.
Вычислить тупой
угол, образованный
медианами,
проведенными
из вершин острых
углов равнобедренного
прямоугольного
треугольника.
адача.
Вычислить тупой
угол, образованный
медианами,
проведенными
из вершин острых
углов равнобедренного
прямоугольного
треугольника.
Решение.
Пусть
![]() и
и
![]() ;
;
Согласно
условию ![]() .
.
Вектор
![]() есть
разность векторов
есть
разность векторов
![]() и
и ![]() ,
т.е.
,
т.е. ![]() (т.к.
(т.к.
![]() ).
).
Угол между векторами находится по формуле:
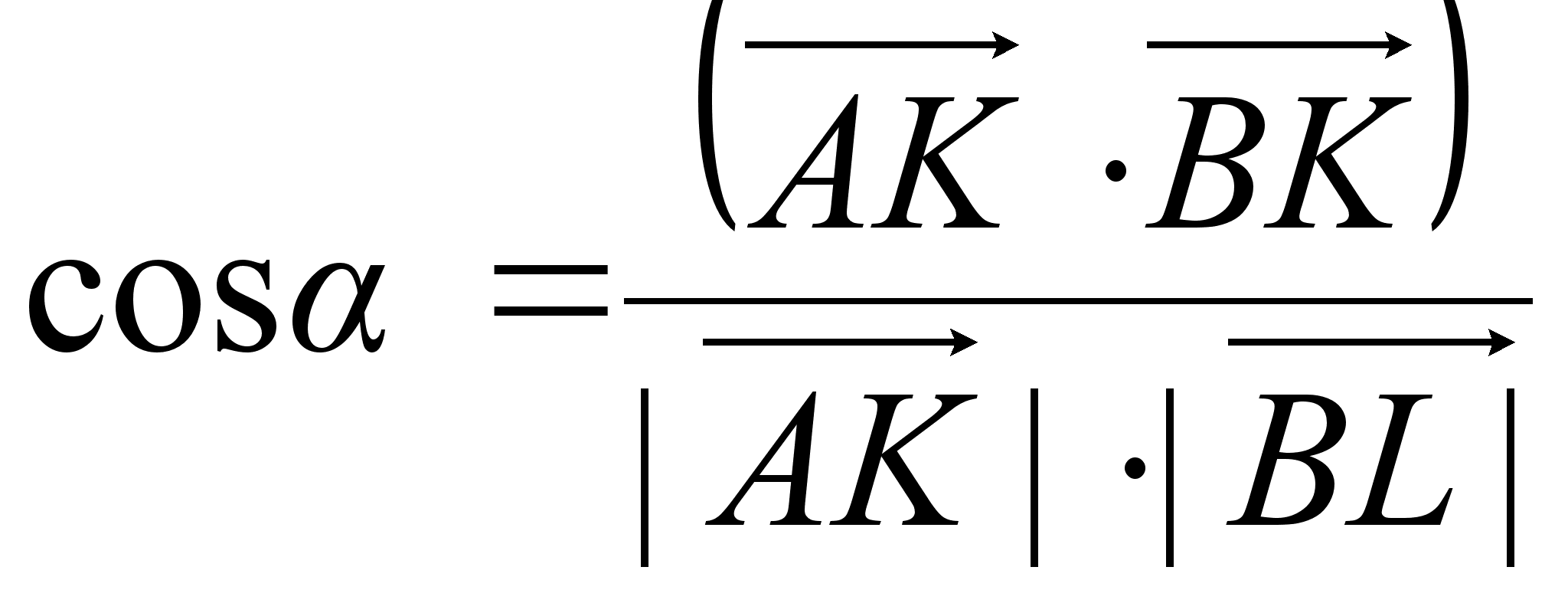
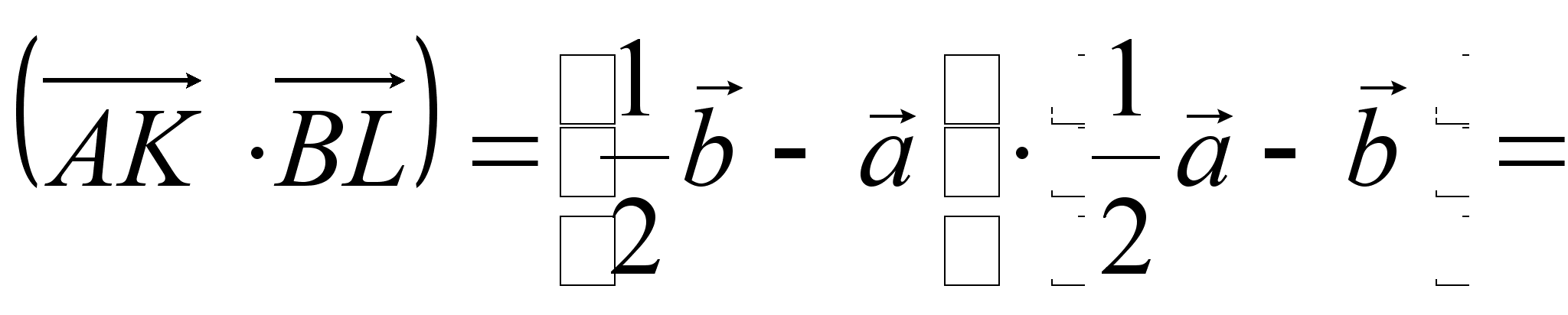
![]() ,
,
но, ![]() ,
т.к.
,
т.к. ![]() .
Следовательно
.
Следовательно
![]()
![]() .
.
длины
векторов ![]() и
и
![]() найдем по теореме
Пифагора.
найдем по теореме
Пифагора.
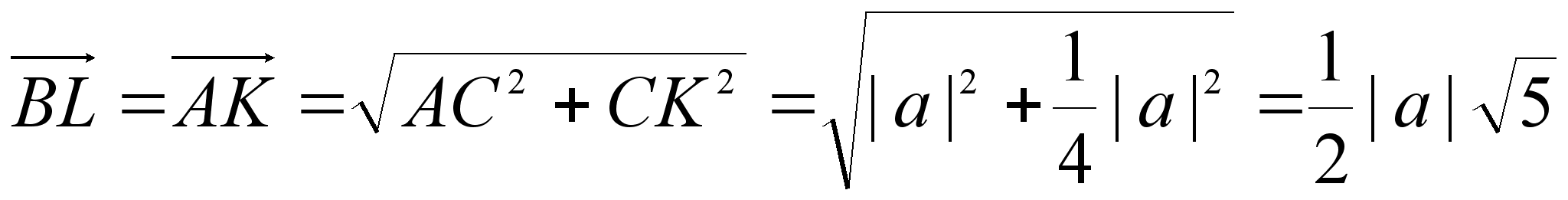
Таким
образом 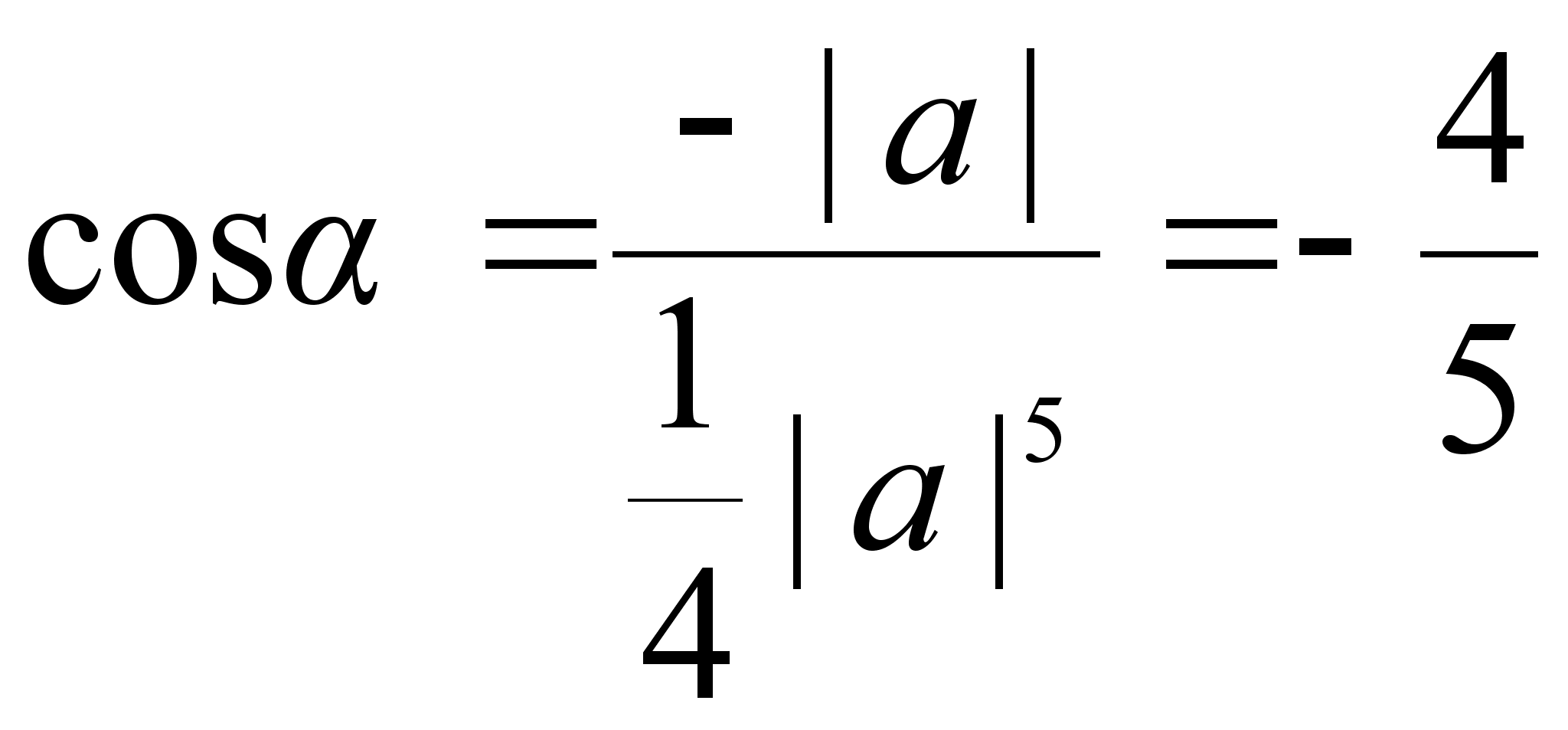
Тогда 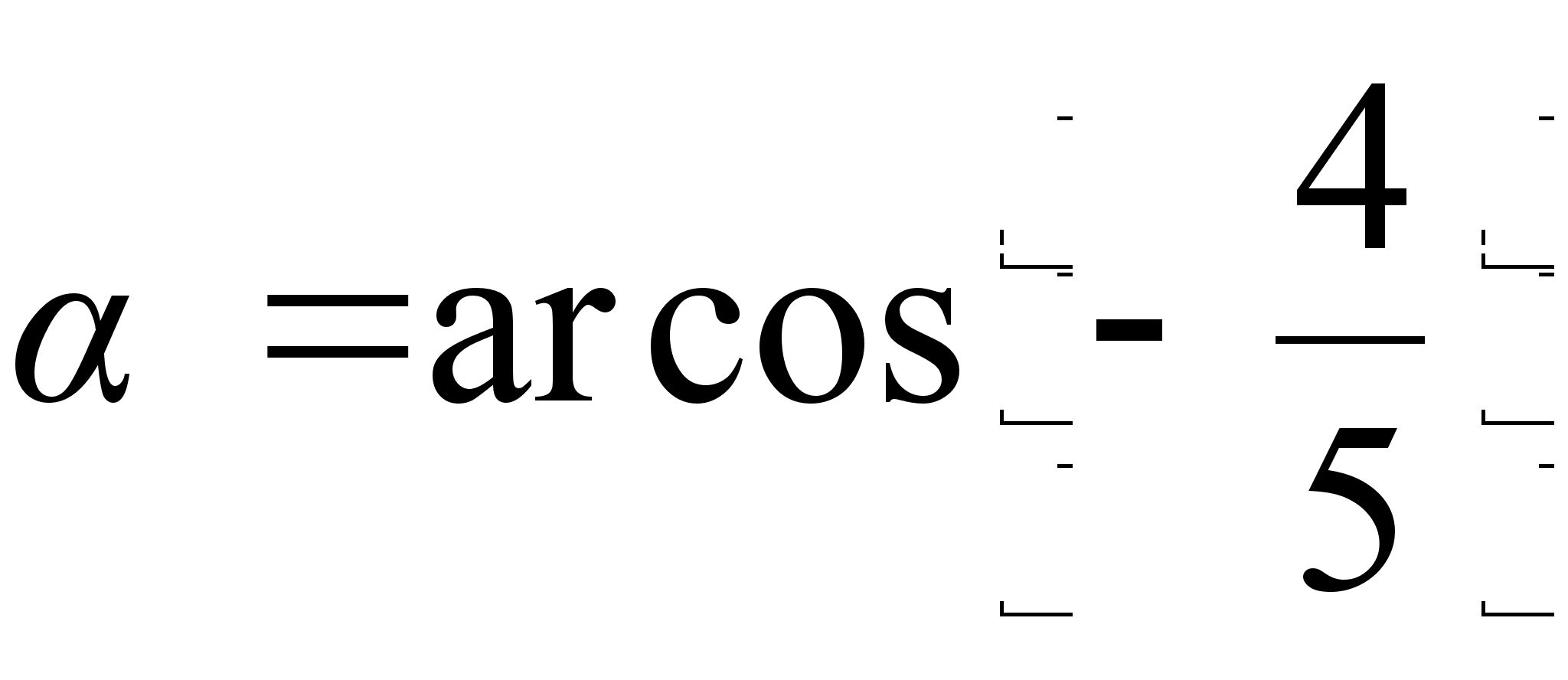
Ответ: 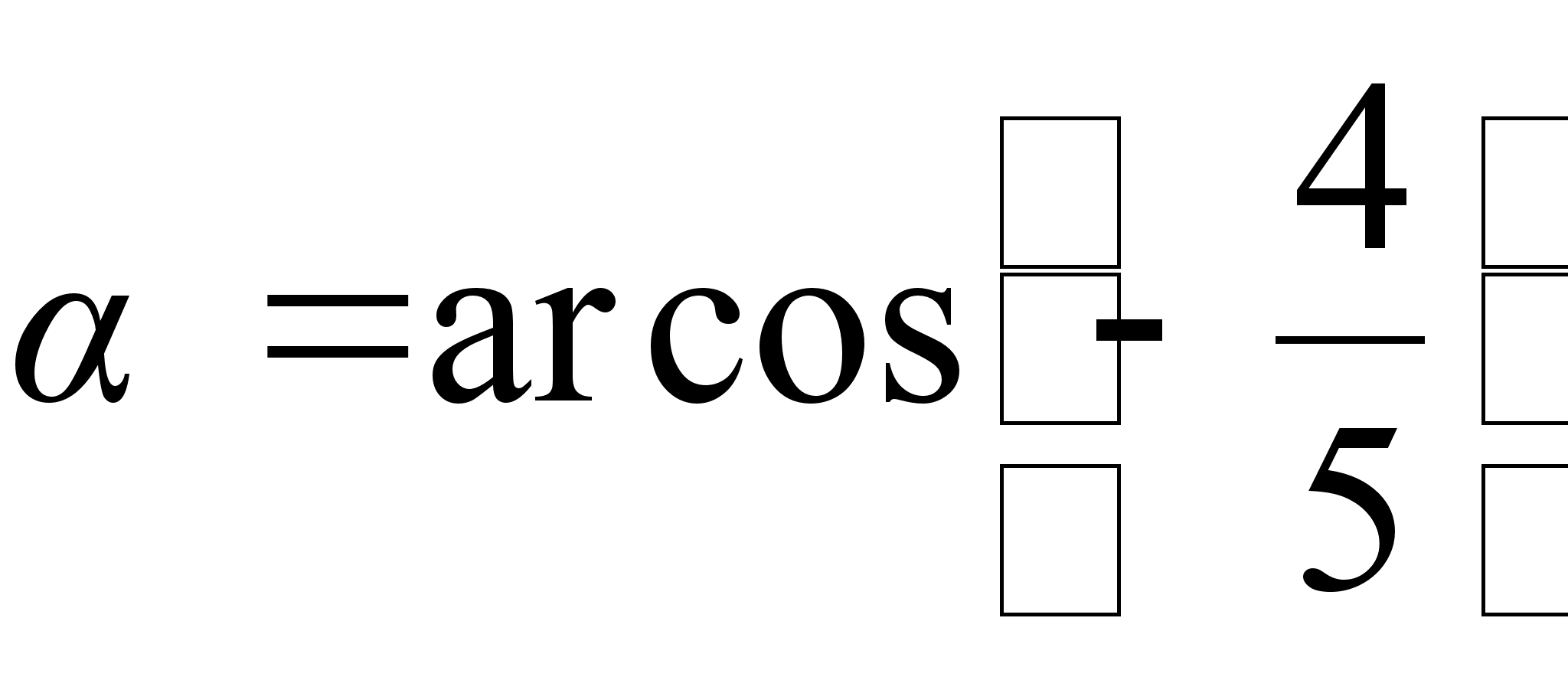
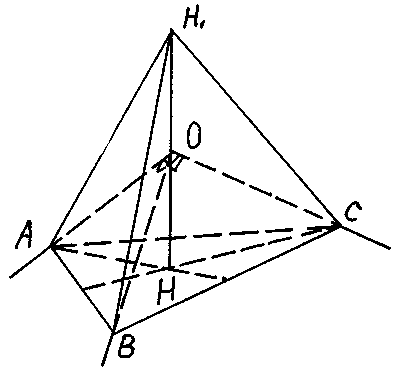
Задача. На ребрах прямоугольного трехгранного угла с вершиной О отложены равные отрезки ОА, ОВ, ОС. Из точки О на плоскости ABC опущен перпендикуляр ОН. Доказать, что если точка Н1 симметрична точке Н относительно вершины О, то тетраэдр Н1 ABC правильный.
Решение:
Примем вершину О трехгранного угла за начало векторов. Тогда
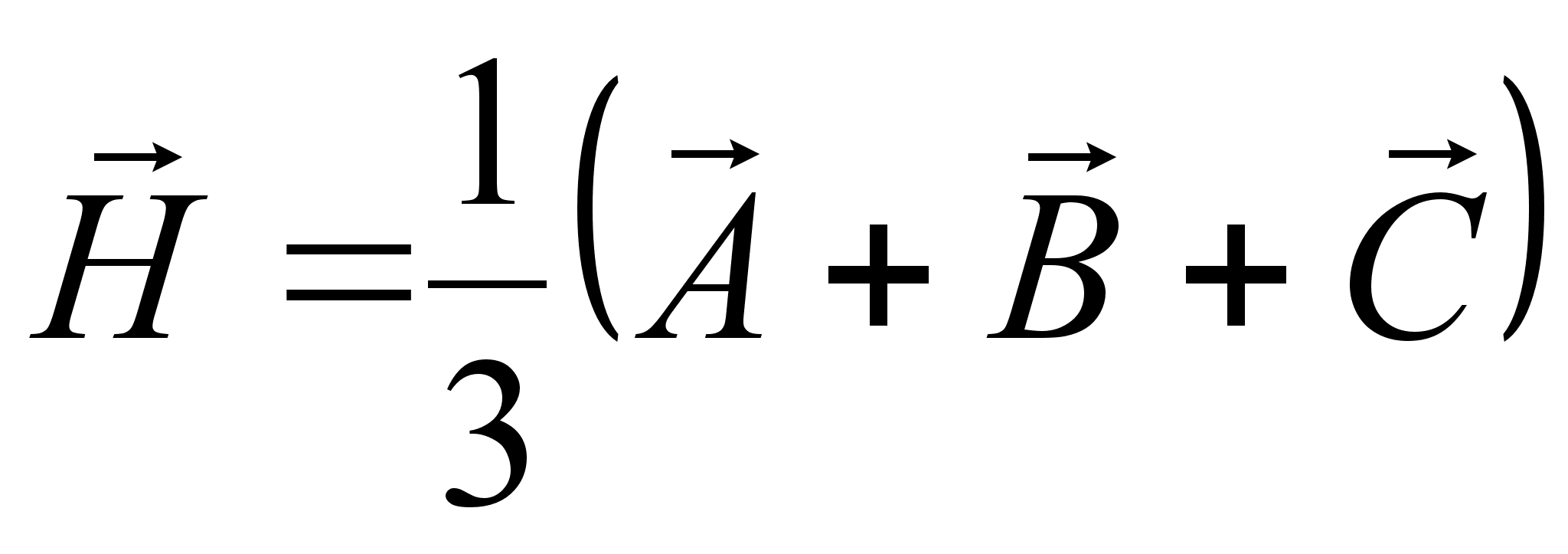
 и
и 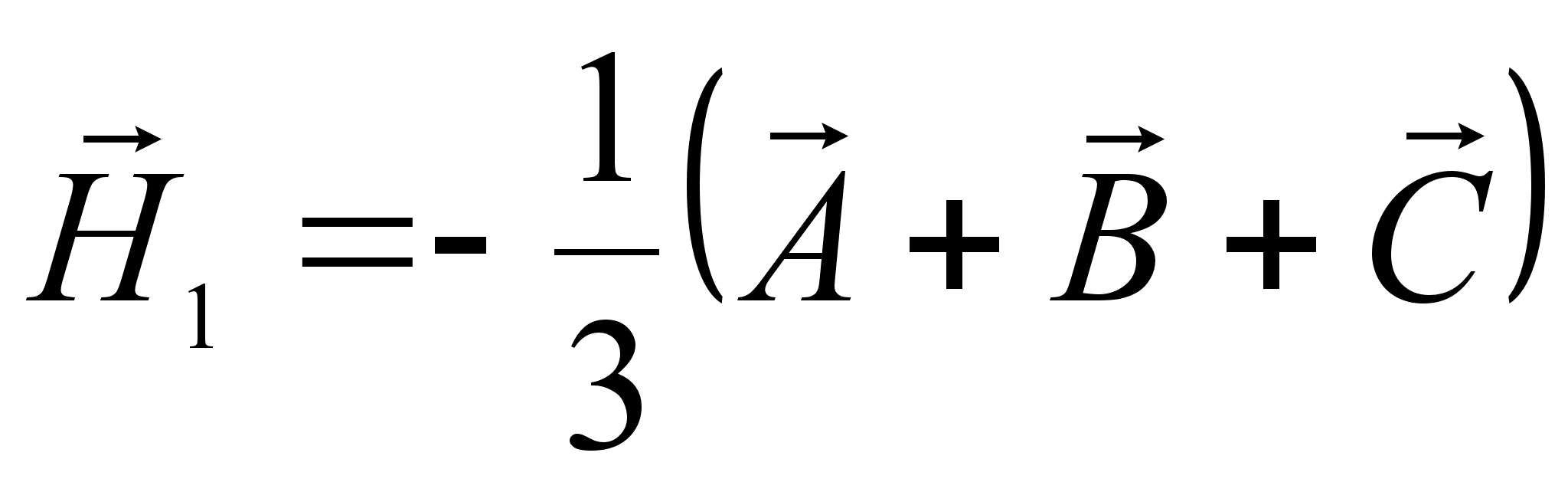 .
.
Следовательно,
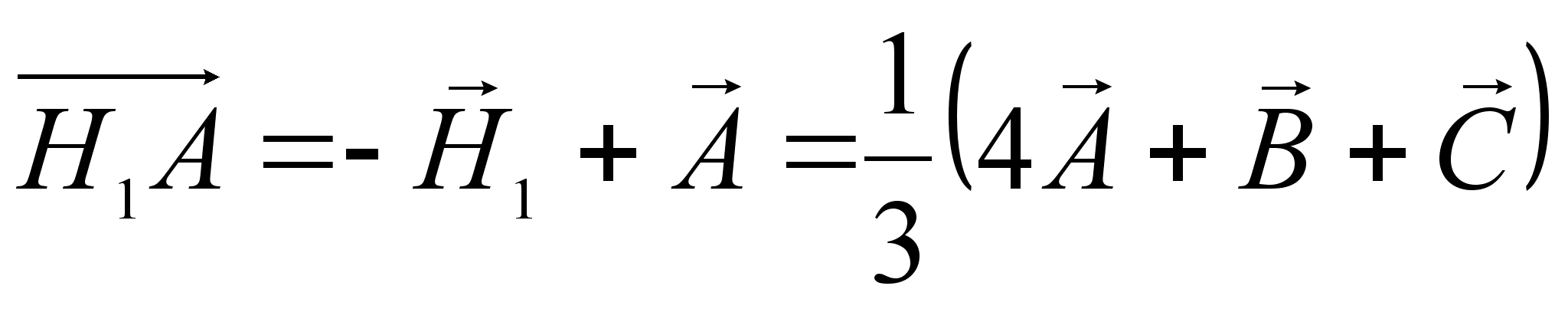 ,
,
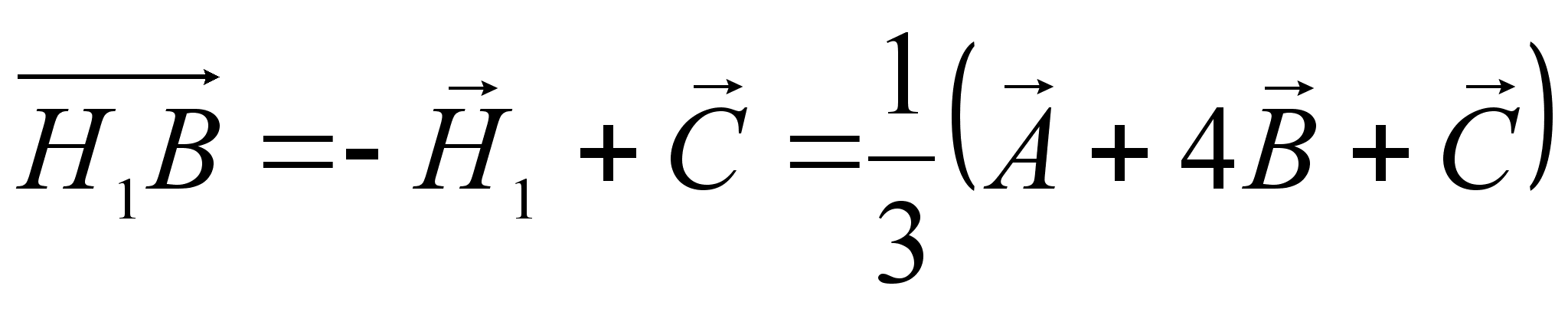 .
.
Найдем
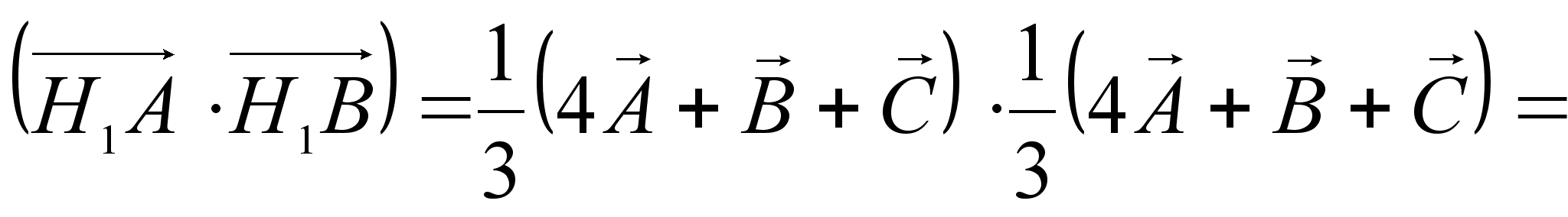
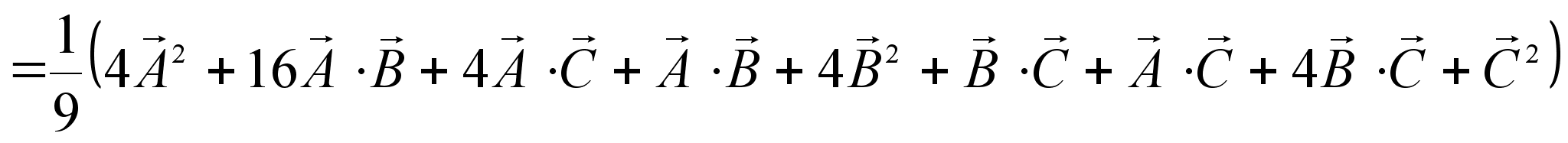
Учитывая,
что ![]() и
и ![]() ,
имеем:
,
имеем: 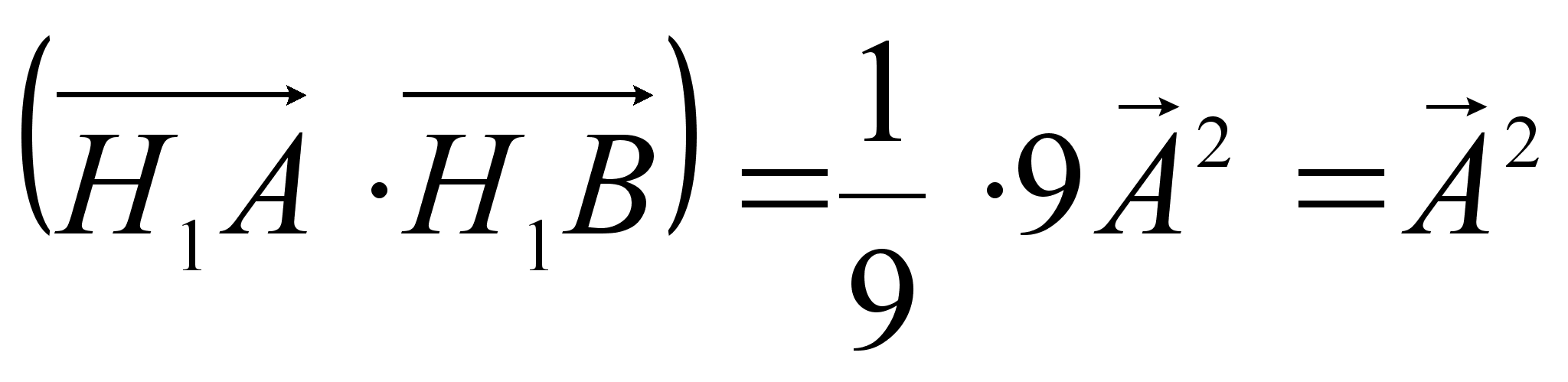 .
.
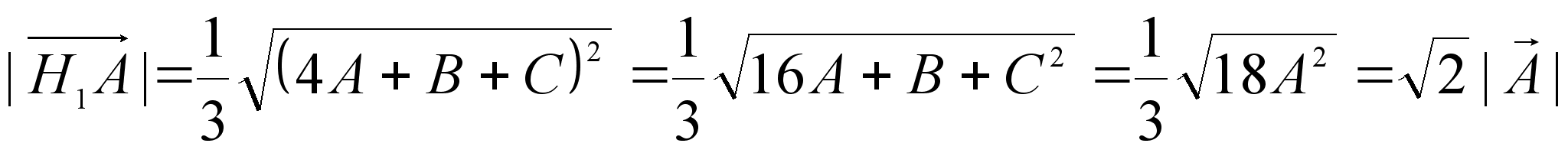 ,
,
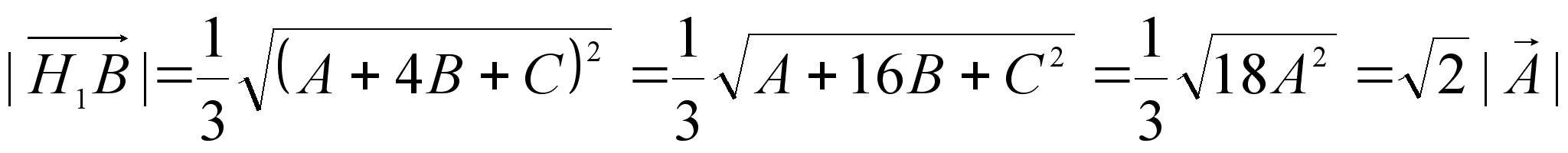 ,
,
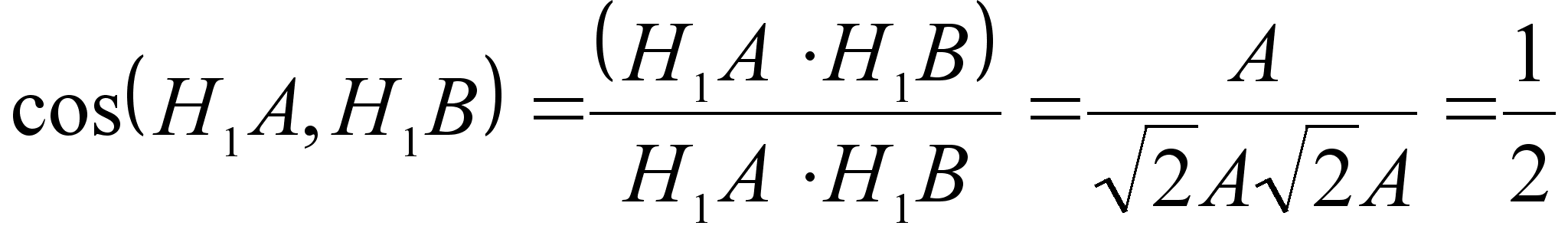 .
.
Это значит , что отрезки H1A и H1B равны и образуют угол 60°, т.е. треугольник H1AB правильный.
Аналогично устанавливается, что две другие грани H1BC и H1CA являются равносторонними треугольниками и вследствие этого тетраэдр правильный.
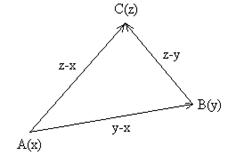
Задача. Доказать, что можно построить треугольник, стороны которого равны и параллельна медианам данного треугольника ABC.
Решение.
О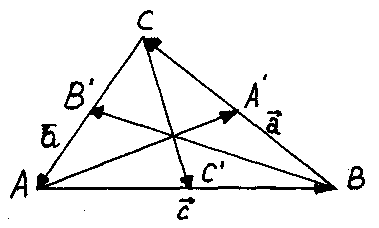 бозначим
середины сторон
ВС,
СА
и АВ
соответственно
А’,
B’,
C’.
Выразим векторы,
представляющие
медианы треугольника
ABC,
через
бозначим
середины сторон
ВС,
СА
и АВ
соответственно
А’,
B’,
C’.
Выразим векторы,
представляющие
медианы треугольника
ABC,
через ![]() ,
,
![]() ,
,
![]() (через стороны
данного треугольника):
(через стороны
данного треугольника):
![]() ,
,
![]() ,
,
![]() .
.
Составим сумму сторон треугольника ABC
![]() .
.
Но так
как векторы
![]() и
и
![]() образуют
данный треугольник
ABC,
то их сумма
равна нулю,
следовательно,
и
образуют
данный треугольник
ABC,
то их сумма
равна нулю,
следовательно,
и ![]() .
А это значит,
что из векторов
.
А это значит,
что из векторов ![]() можно построить
треугольник.
можно построить
треугольник.
З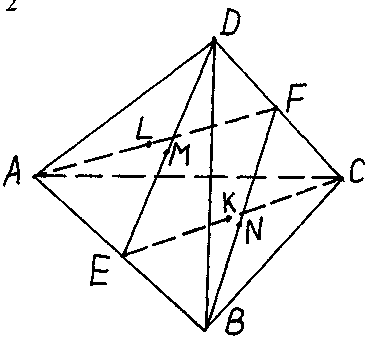 адача.
В треугольнике
ABCD
точка
Е
и F
– середина
рёбер АВ
и CD
соответственно.
Доказать, что
середины отрезков
СЕ,
DE,
AF
и
BF
являются
вершинами
параллелограмма.
адача.
В треугольнике
ABCD
точка
Е
и F
– середина
рёбер АВ
и CD
соответственно.
Доказать, что
середины отрезков
СЕ,
DE,
AF
и
BF
являются
вершинами
параллелограмма.
Решение. Пусть К, L, М, N - середины отрезков СЕ, DE, AF и BF, соответственно. Доказать, что середины отрезков СЕ, DE, AF и BF являются вершинами параллелограмма.
Докажем
равенство
векторов ![]() и
и
![]() ,
выразив
их через векторы
,
выразив
их через векторы
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где
О
– произвольная
точка.
,
где
О
– произвольная
точка.
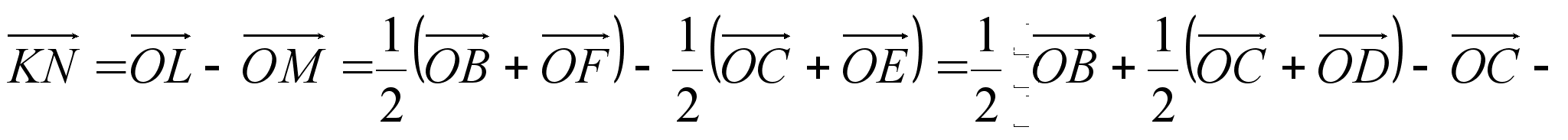
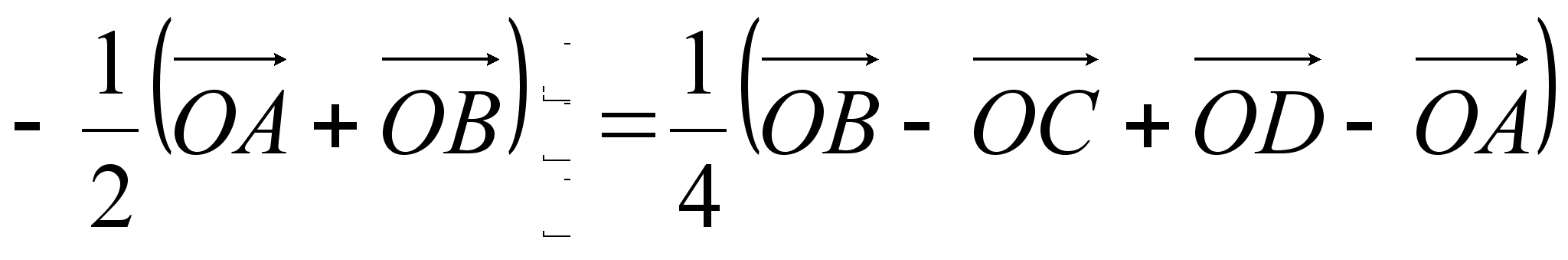 (1)
(1)
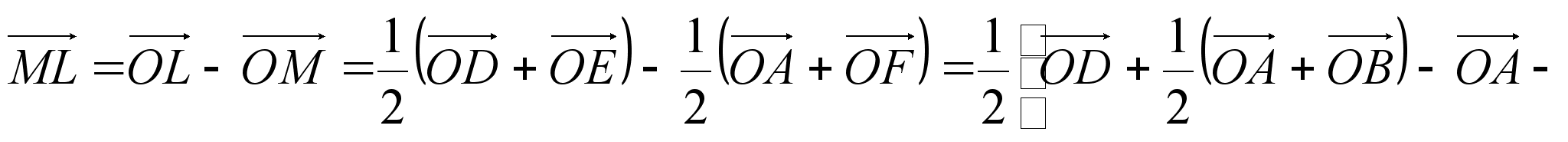
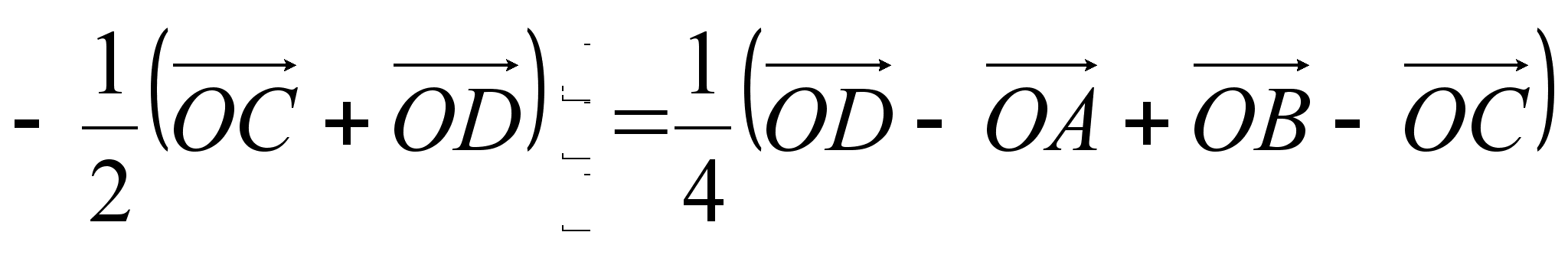 . (2)
. (2)
Ч. Т. Д.
Задача.
Точки К,
L,
M
на сторонах
АС,
ВС,
АВ
треугольника
ABC
таковы, что 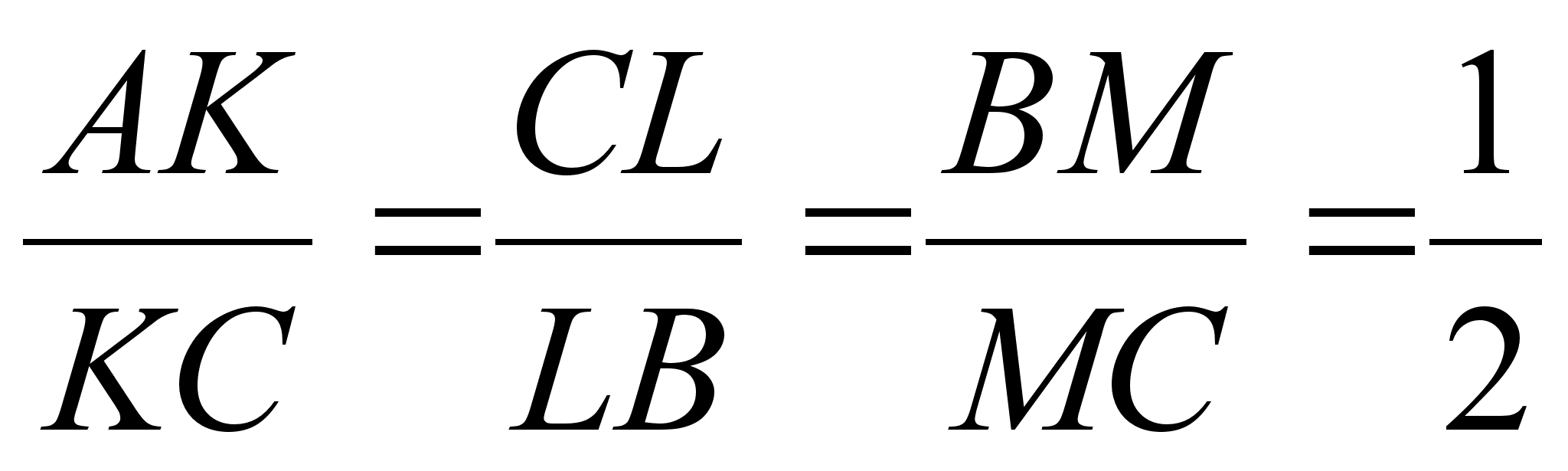 , N
– середина сторона АС. Найти отношение
в котором точка
пересечения
отрезков KL
и MN
делит отрезок
KL.
, N
– середина сторона АС. Найти отношение
в котором точка
пересечения
отрезков KL
и MN
делит отрезок
KL.
Решение.
Обозначим
через О
точку пересечения
отрезков MN
и KL
и через х
отношение KO
: KL.
Тогда ![]() .
Учитывая, что
L
– середина МС
и
.
Учитывая, что
L
– середина МС
и ![]() ,
получаем
,
получаем
![]()
Так
как точка О
лежит на прямой
MN,
то ![]() .
Откуда
.
Откуда ![]() .
Значит,
.
Значит, 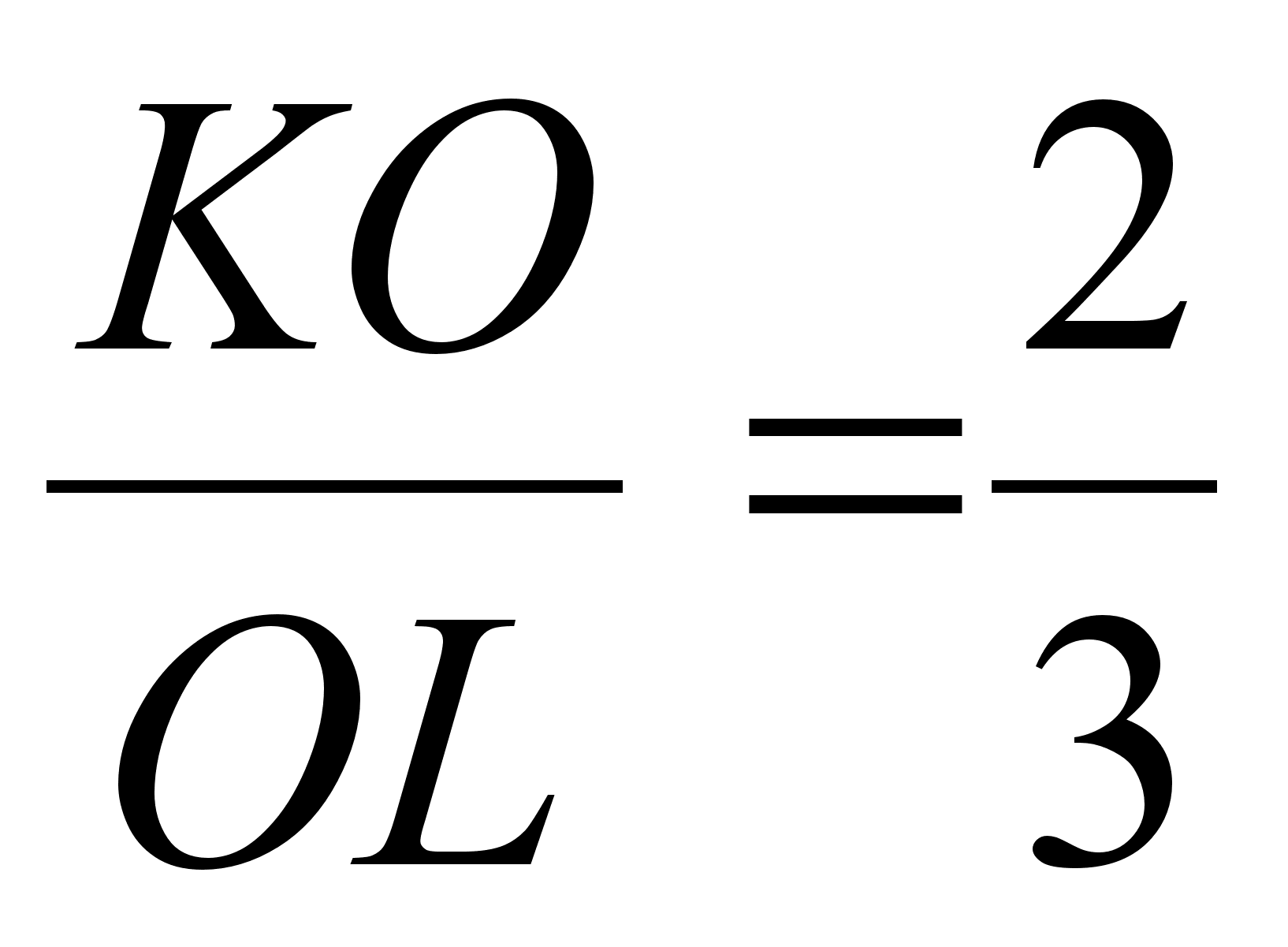 .
.
Ответ: KO : OL = 2:3
З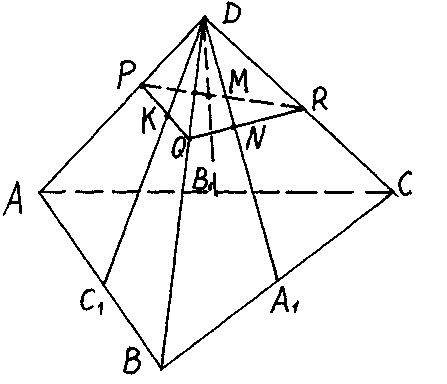 адача.
Отрезки DA1,
DB1,
DC1
– медианы граней
BCD,
ACD
и ABD
тетраэдра ABCD
соответственно.
Точки К,
М,
N
делят отрезки
DA1,
DB1,
DC1
в
отношении
адача.
Отрезки DA1,
DB1,
DC1
– медианы граней
BCD,
ACD
и ABD
тетраэдра ABCD
соответственно.
Точки К,
М,
N
делят отрезки
DA1,
DB1,
DC1
в
отношении 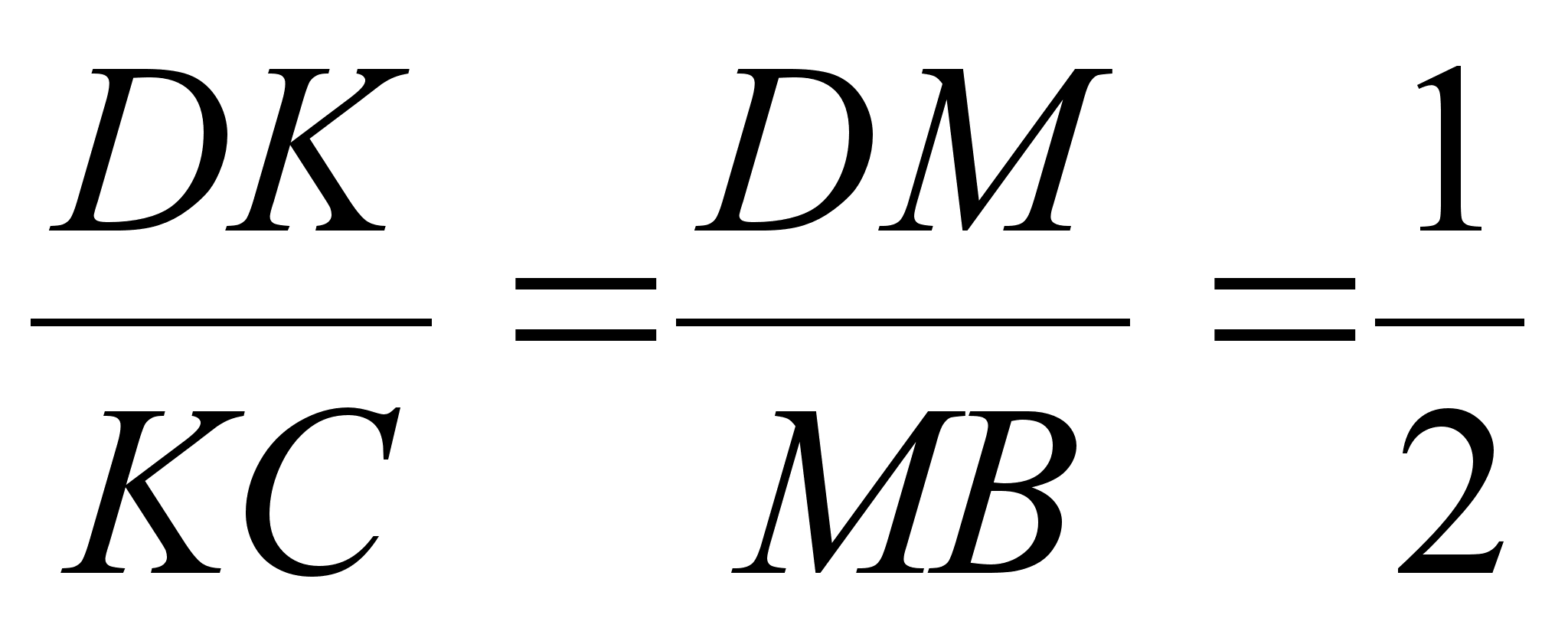 ,
,
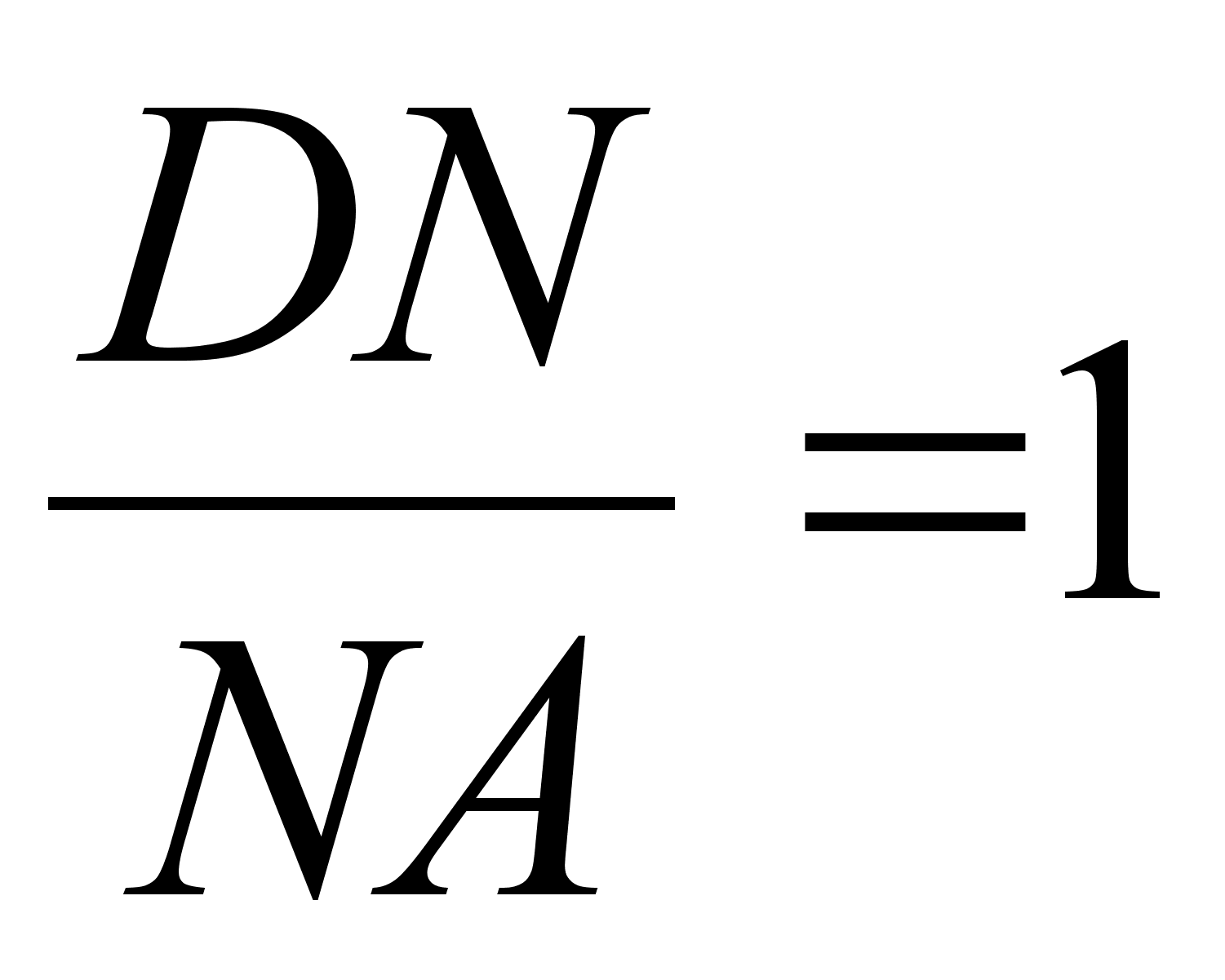 . В каком отношении
плоскость KMN
делит ребра
DA
и DB
?
. В каком отношении
плоскость KMN
делит ребра
DA
и DB
?
Решение.
Пусть плоскость KMN пересекает ребра DA, DB и DC тетраэдра ABCD в точках Р, Q, R соответственно.
Точки А1, В1, С1 – середины отрезков ВС, АС, АВ соответственно. Следовательно,
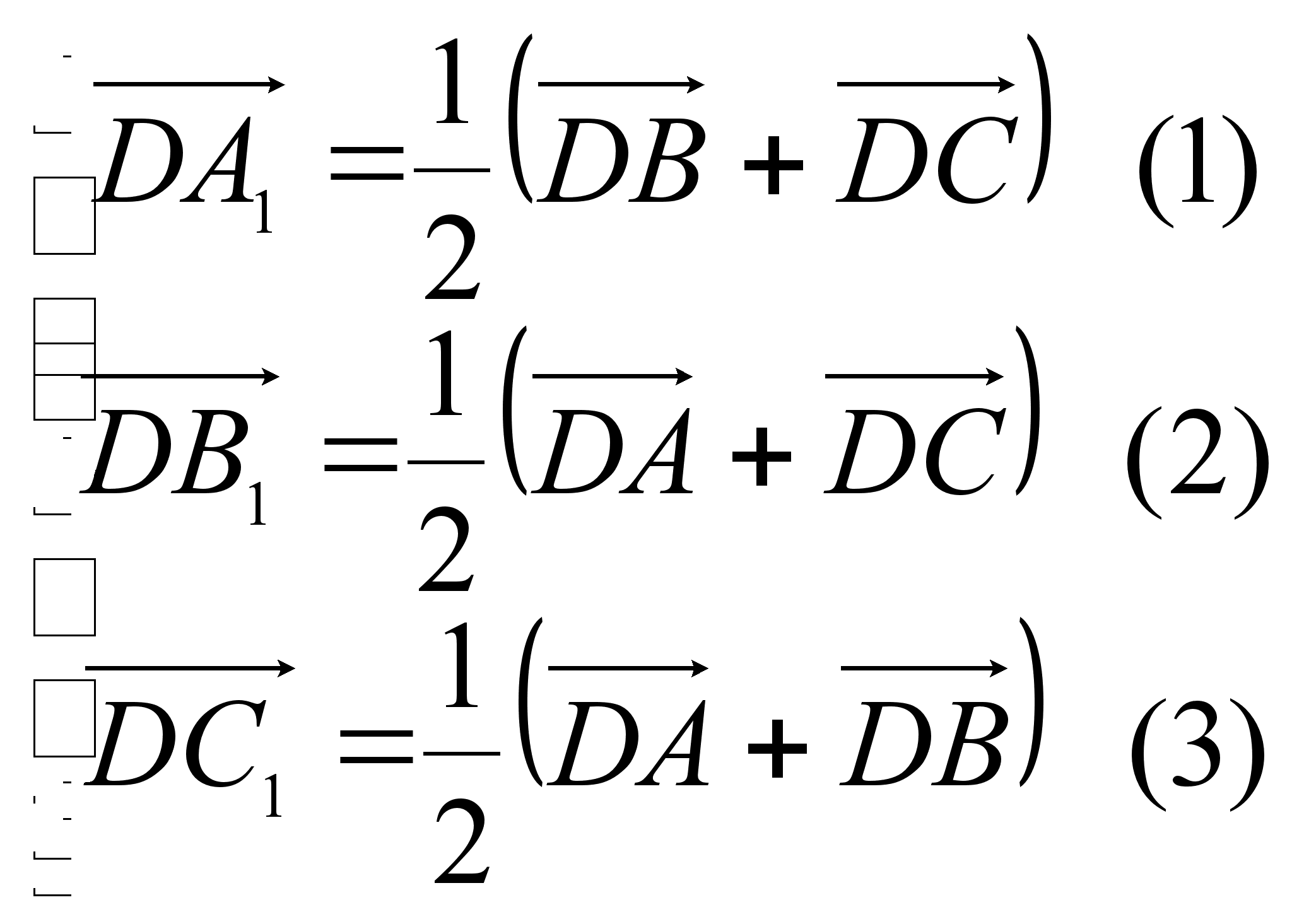
Решив эту систему, (например, сложив (1) и (2), и вычтя (3) получим
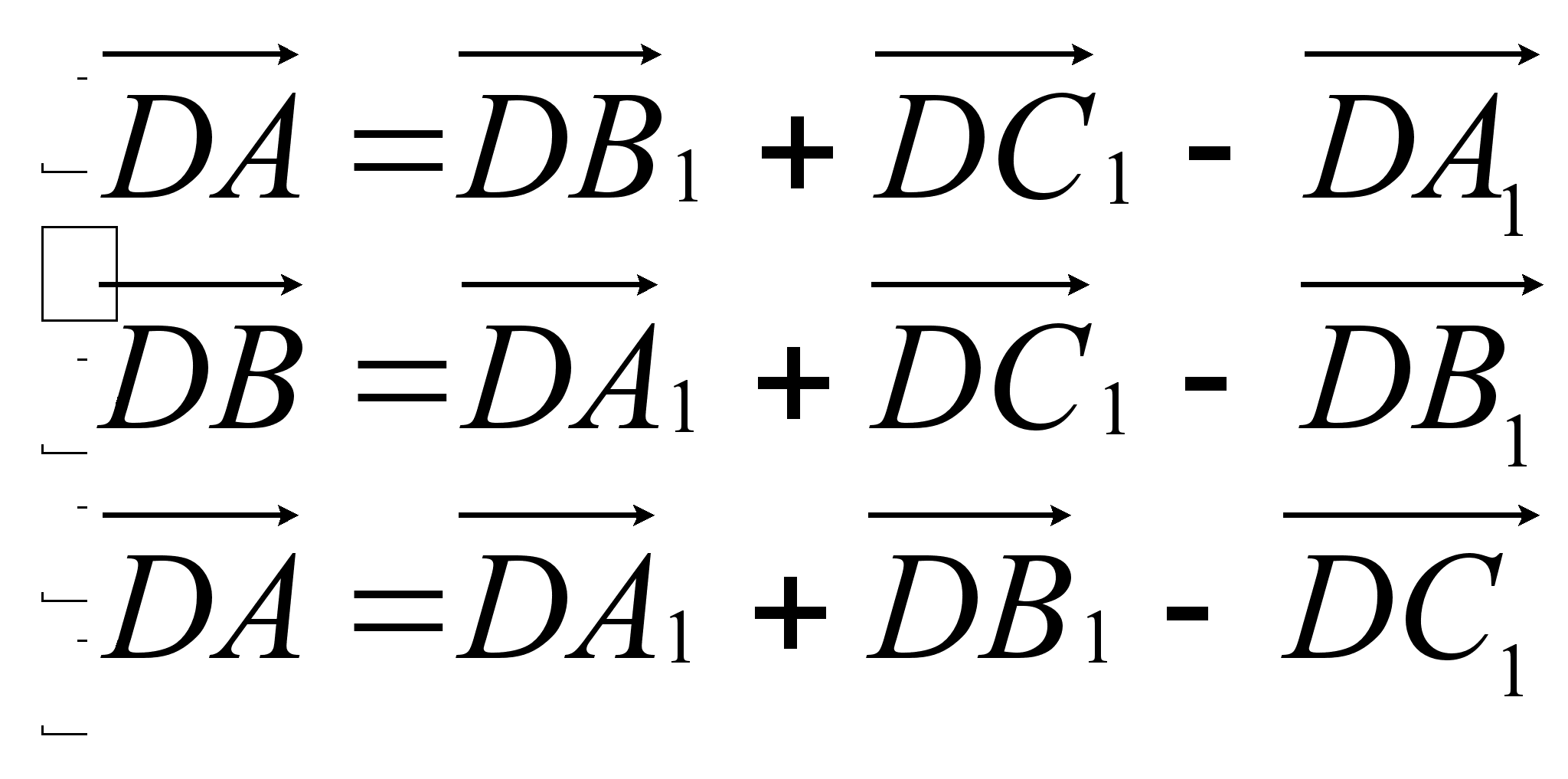
Пусть
![]() .
Тогда, учитывая
.
Тогда, учитывая
![]() ,
,
![]() ,
,
![]() ,
,
имеем
![]() ,
и, т.к. точки К,
М,
N,
Р
лежат в одной
плоскости, то
,
и, т.к. точки К,
М,
N,
Р
лежат в одной
плоскости, то
![]() .
.
Таким
образом, ![]() ,
откуда
,
откуда 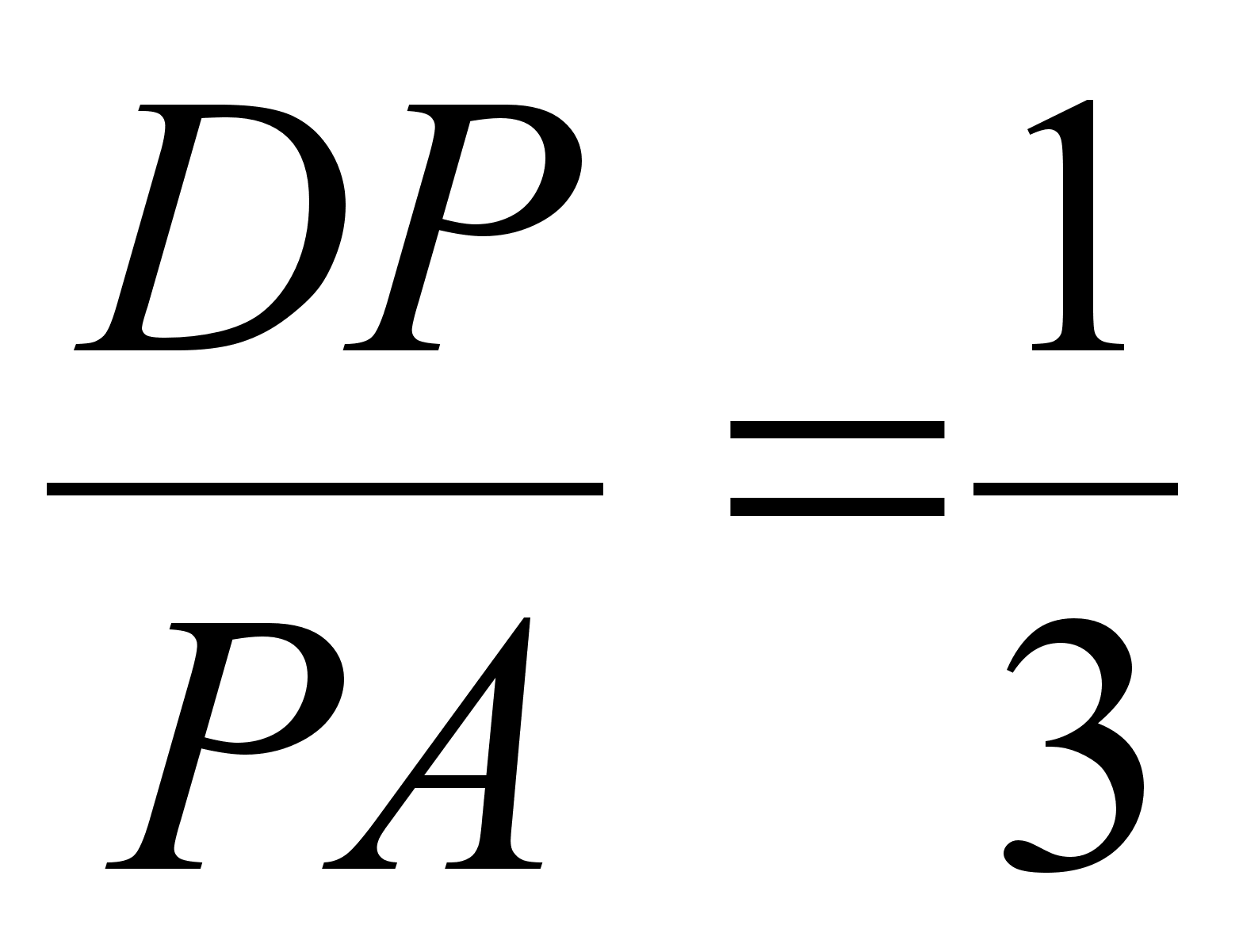 .
.
Пусть
теперь ![]() ,
тогда
,
тогда
![]() ,
и
,
и
![]() ,
откуда
,
откуда 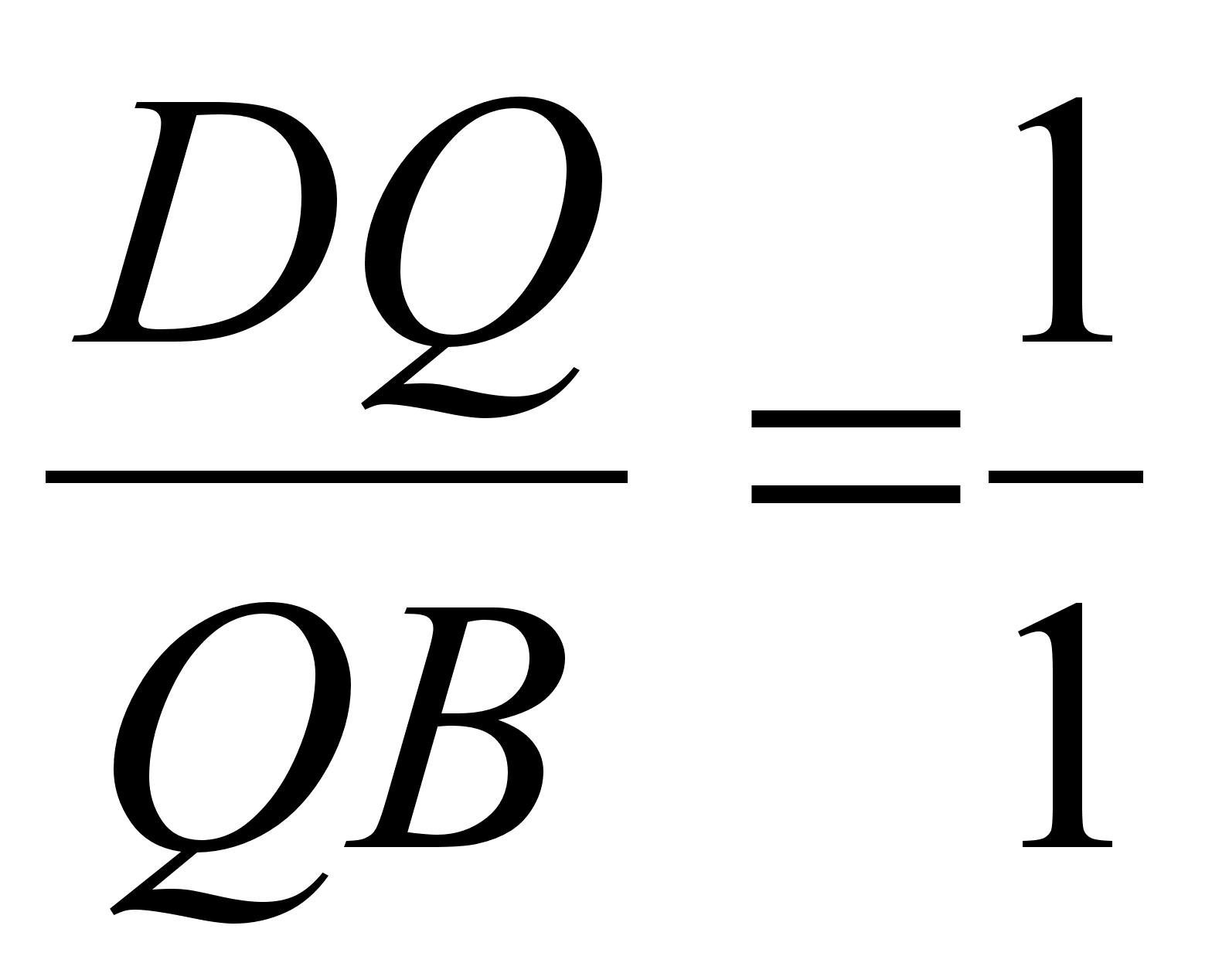
Ответ: 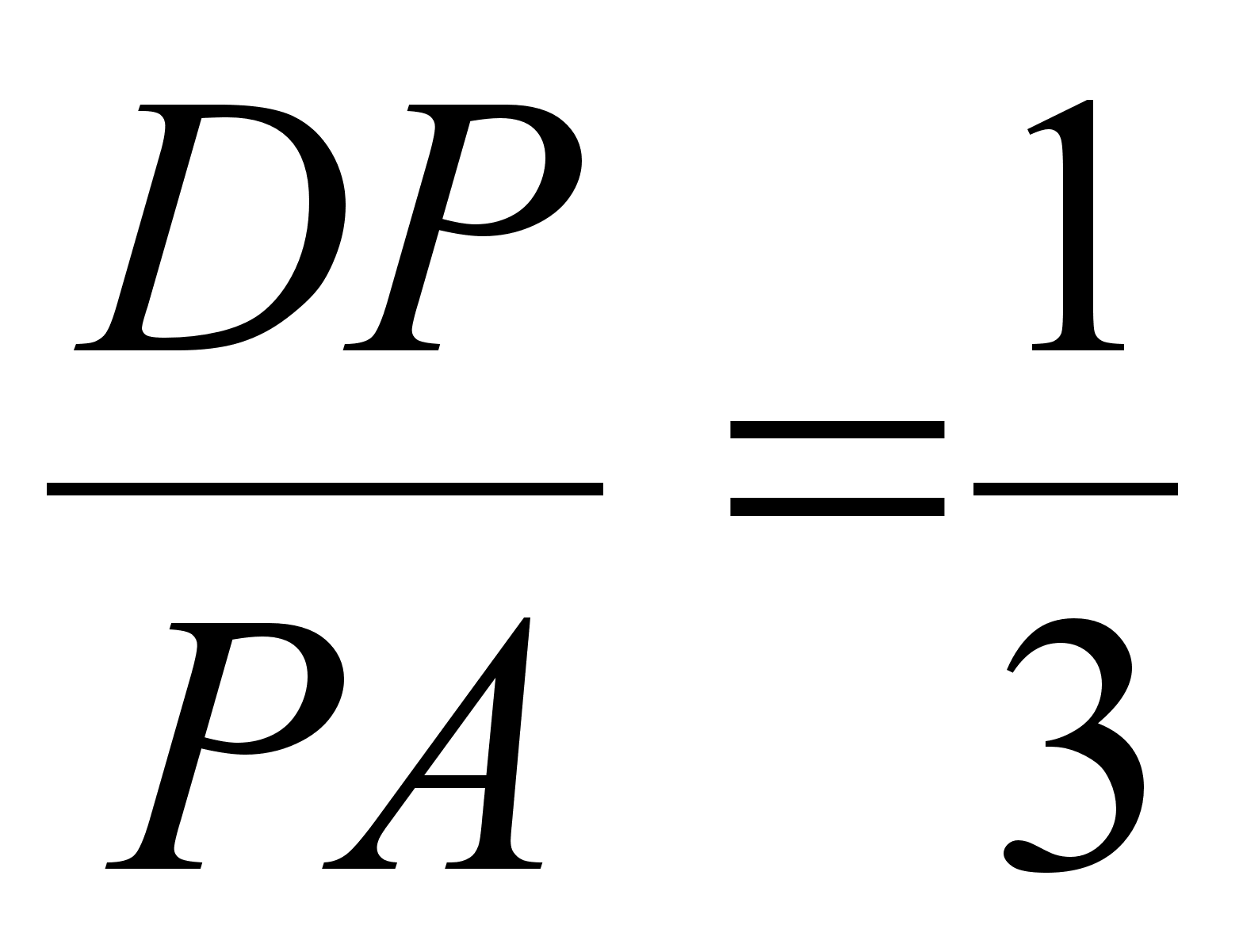 ,
,
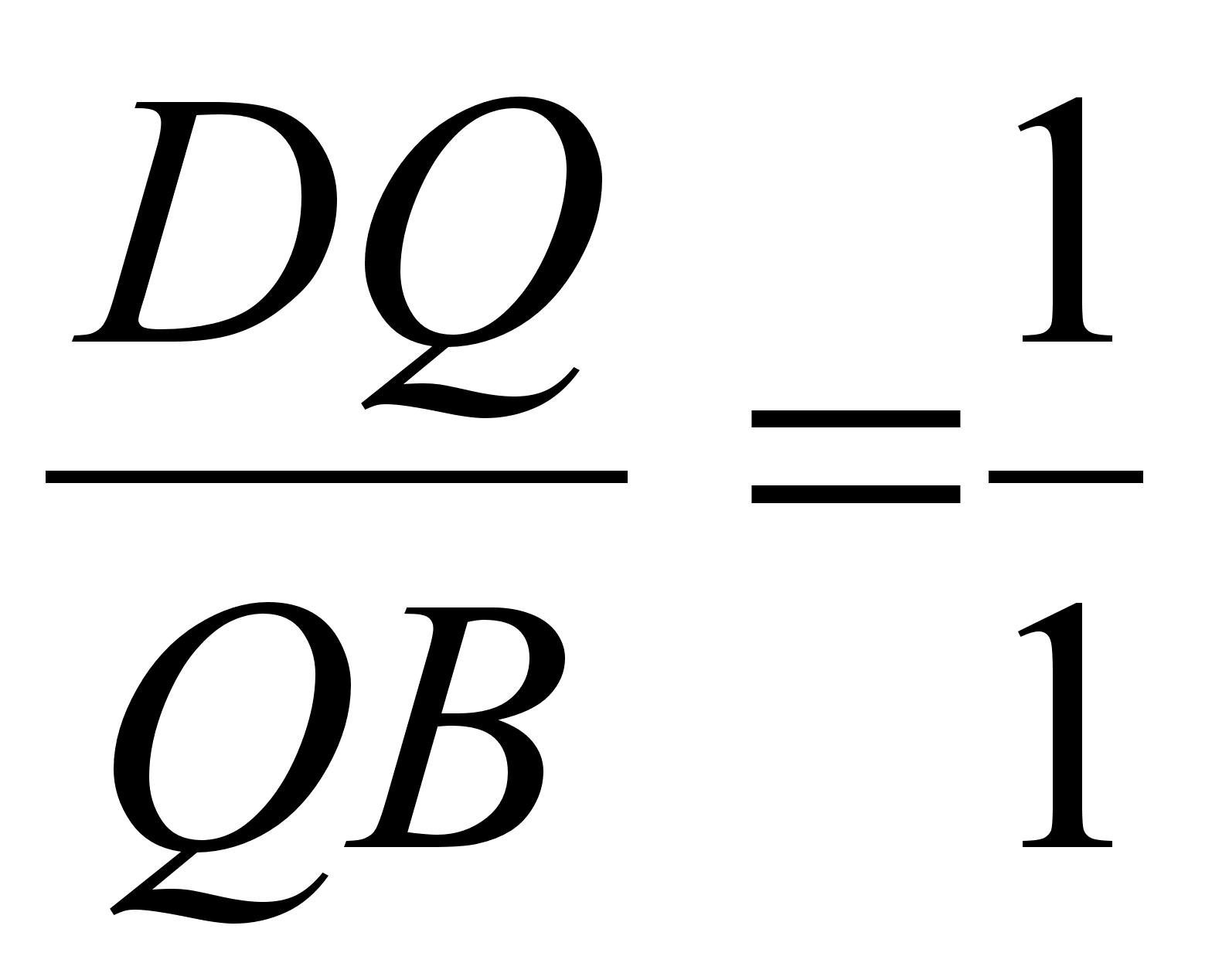 .
.
Задача.
Основанием
пирамиды SABC
является
равносторонний
треугольник
ABC,
длина стороны
которого равна
![]() .
Боковое ребро
SC
перпендикулярно
плоскости
оснований и
имеет длину
2. Найти угол
между прямыми,
одна из которых
проходит через
точку S
и середину
ребра ВС,
а друга проходит
через точку
С
и середину
ребра АВ.
.
Боковое ребро
SC
перпендикулярно
плоскости
оснований и
имеет длину
2. Найти угол
между прямыми,
одна из которых
проходит через
точку S
и середину
ребра ВС,
а друга проходит
через точку
С
и середину
ребра АВ.
Решение.
Обозначим ![]() .
.
Выберем
в качестве
базиса векторы
![]() ,
,
![]() и
и ![]() .
.
Тогда,
из треугольника
BCS: ![]() ,
,
а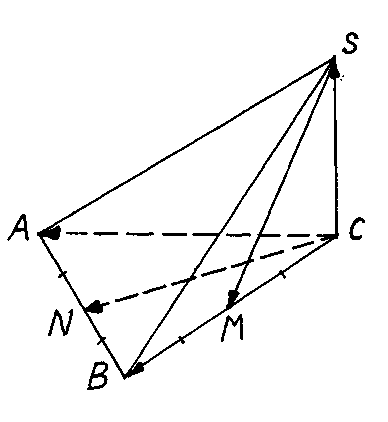 из треугольника
ABC:
из треугольника
ABC: ![]()
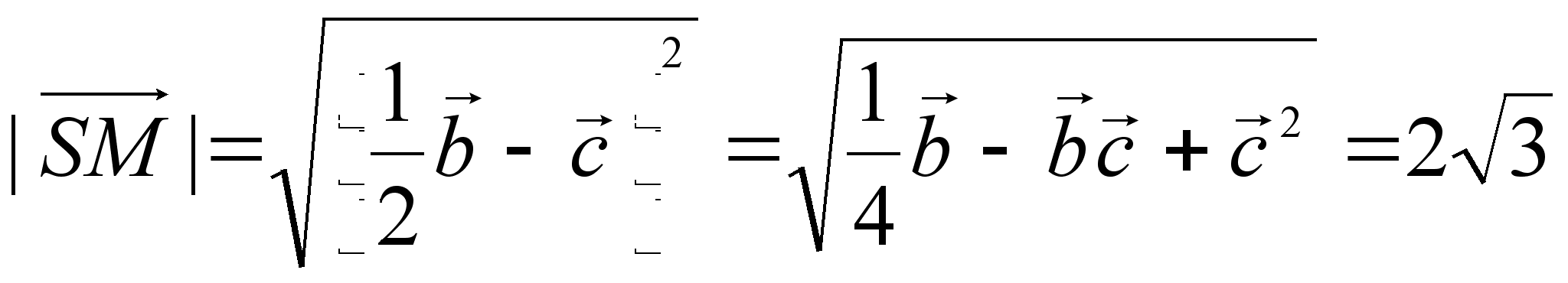
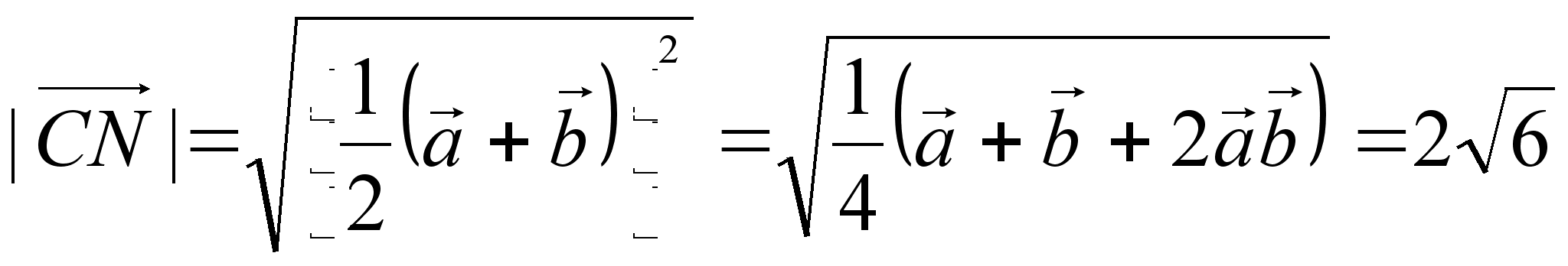
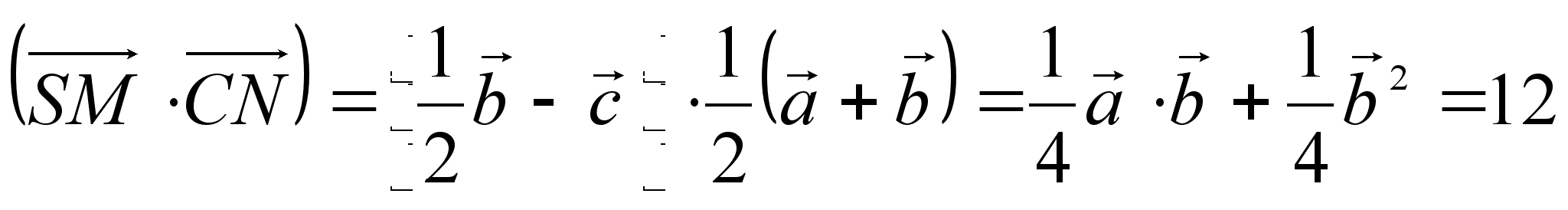
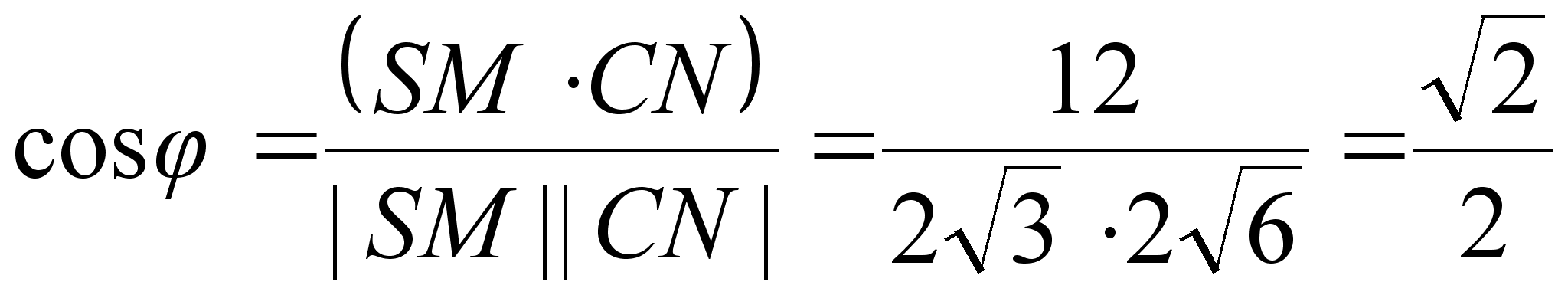
Ответ:
![]() .
.
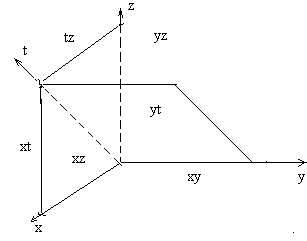
Задача. Каждое ребро призмы ABCA1B1С1 равно 2.
Точки М и N – середины ребер АВ и A1А. Найти расстояние от точки М до прямой CN, если известно, что угол A1AС paвeн 60° и прямые A1A и АВ перпендикулярны.
Решение.
Рассмотрим
базис, состоящий
из векторов
![]() ,
,
![]() ,
,
![]() и
составим таблицу
умножения для
этих векторов.
и
составим таблицу
умножения для
этих векторов.
| * | а | b | с |
| а | 4 | 0 | 2 |
| b | 0 | 4 | 2 |
| с | 2 | 2 | 4 |
Р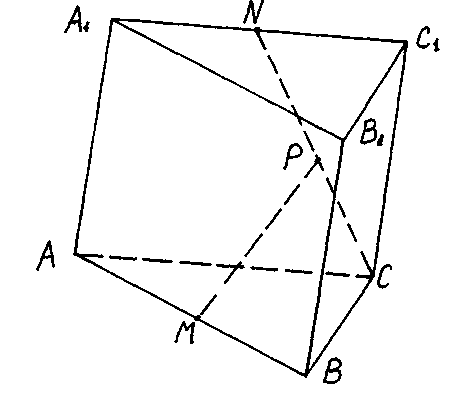 асстояние
от точки М
до прямой CN
равно расстоянию
от точки М
до её проекции
на прямую CN.
асстояние
от точки М
до прямой CN
равно расстоянию
от точки М
до её проекции
на прямую CN.
Пусть Р – проекция точки М на прямую CN.
Тогда
![]()
для некоторого числа х.
Так
как ![]() и
и ![]() ,
,
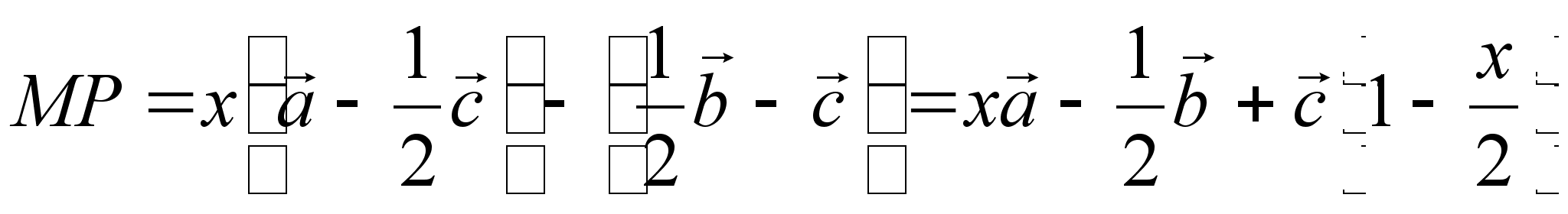
Поскольку
прямые ![]() и
и
![]() перпендикулярны,
то
перпендикулярны,
то ![]() т.е.
т.е.
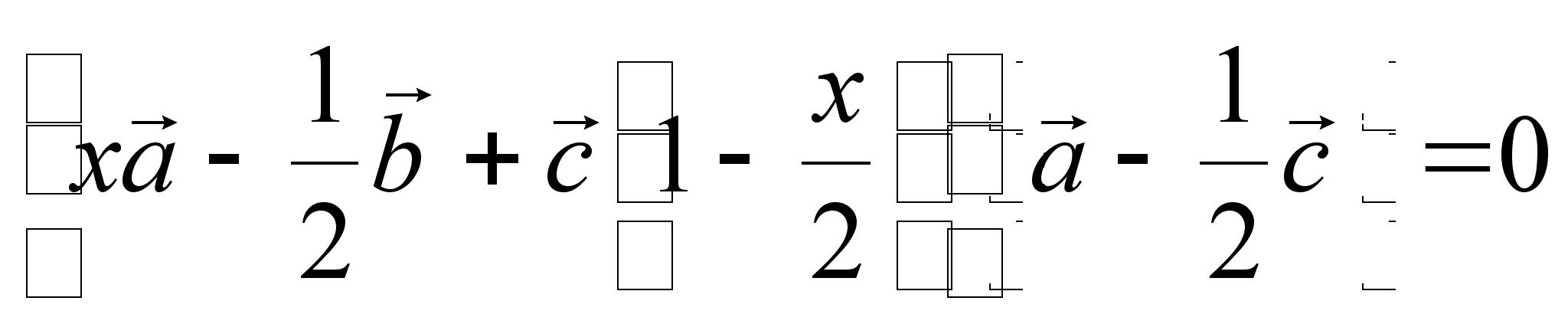 .
.
Раскрывая
скобки и пользуясь
таблицей умножения
для нашего
базиса, получаем: 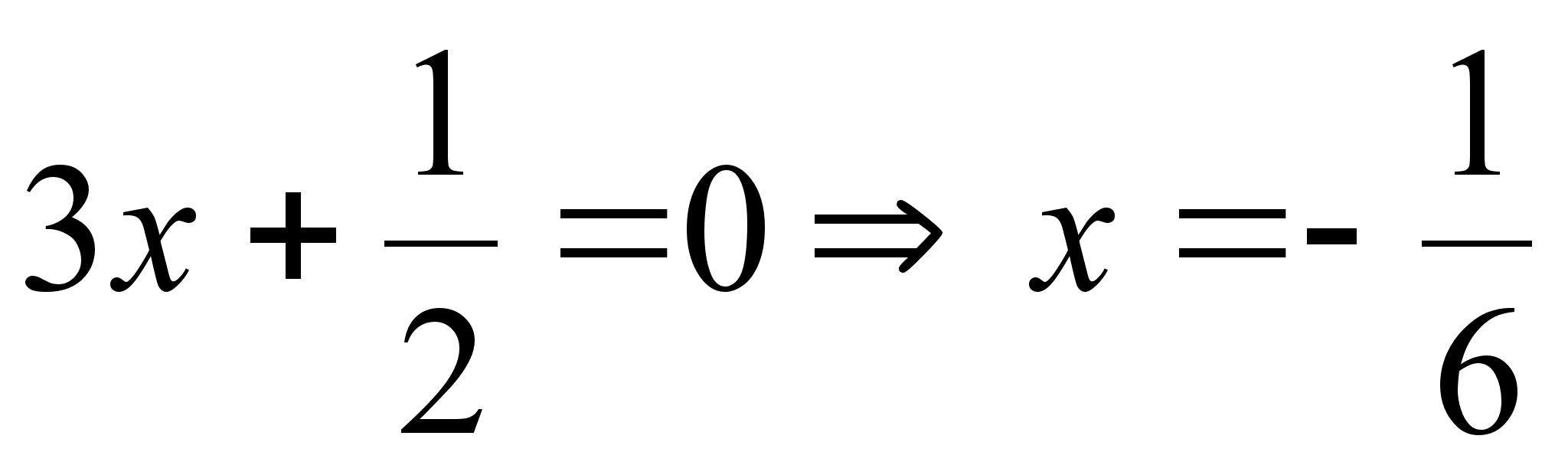 .
.
Тогда
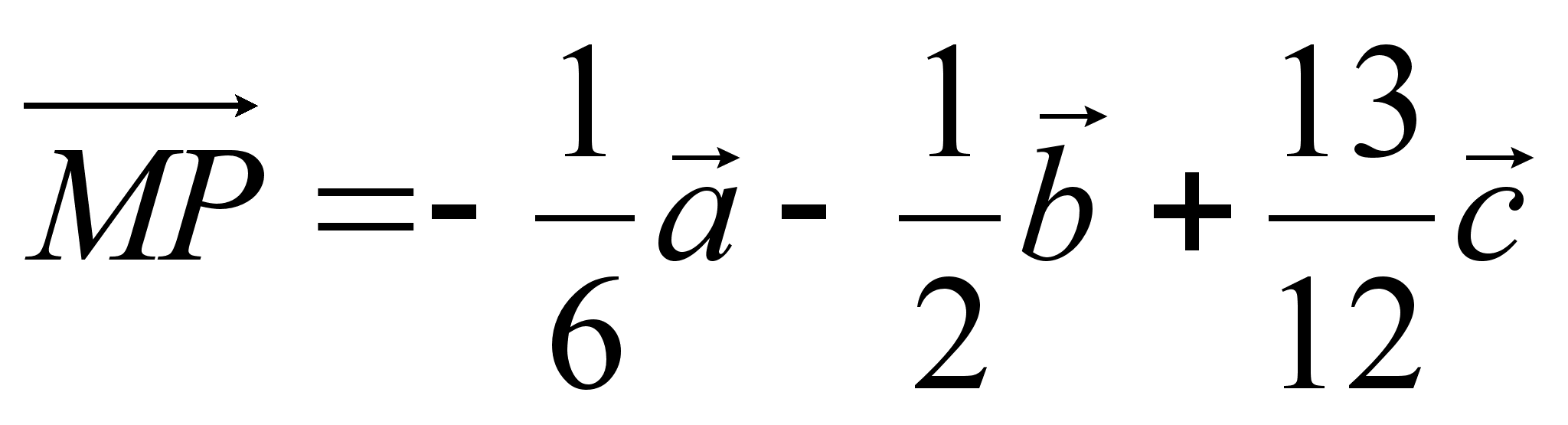 .
.
Искомое
расстояние
![]() равно
равно
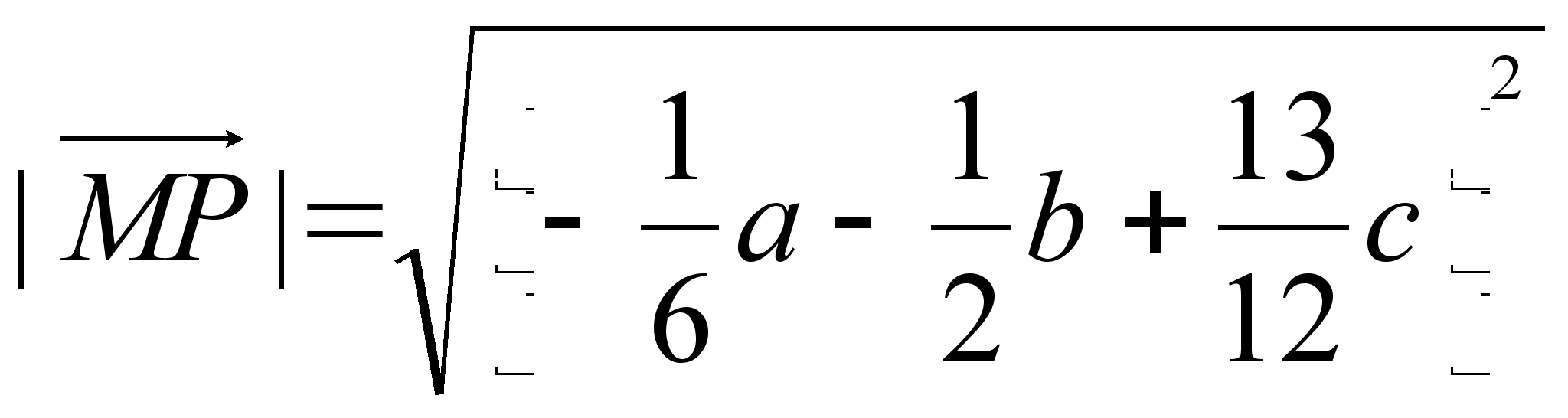
Снова
раскрывая
скобки и пользуясь
таблицей умножения,
находим 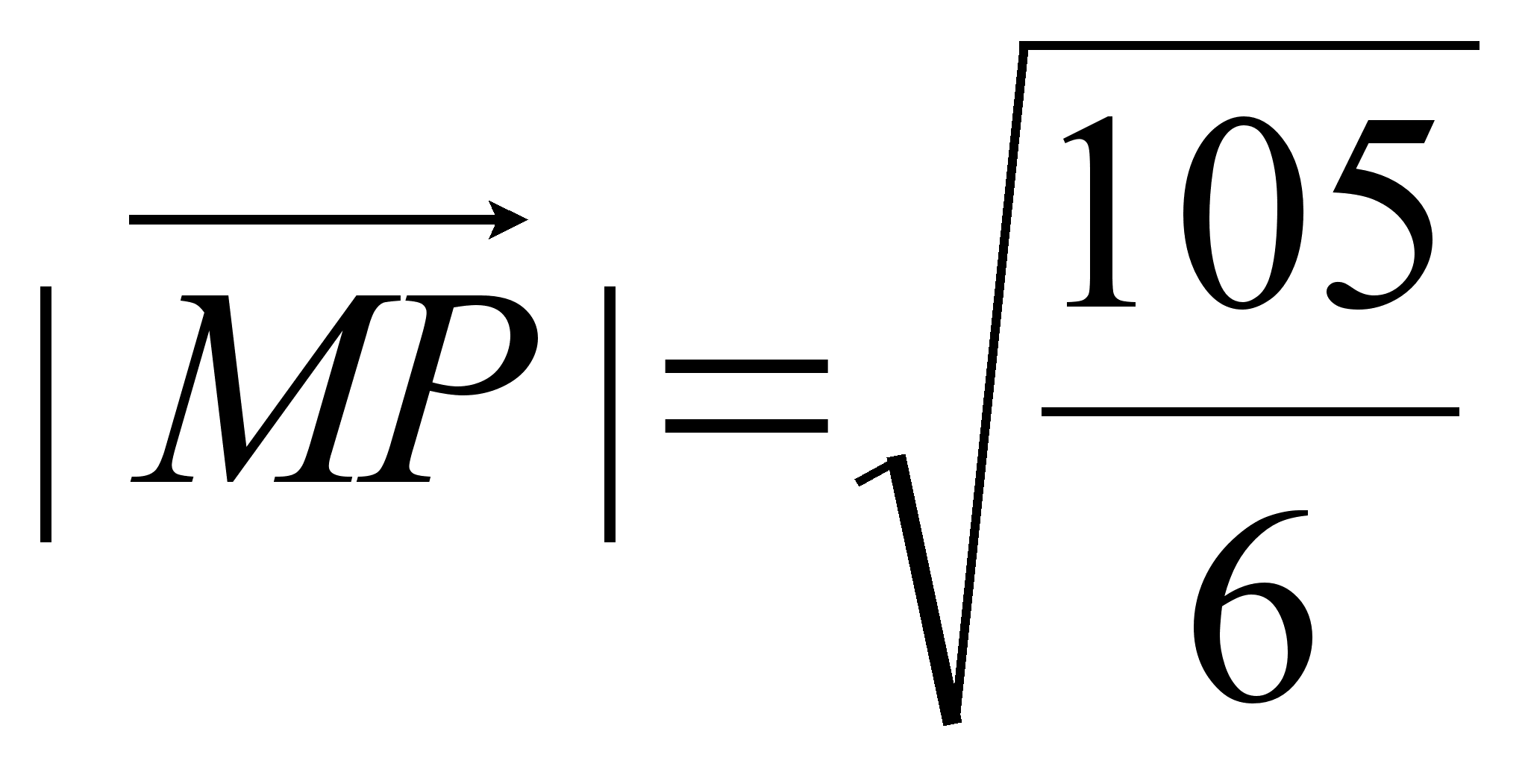 .
Таким
образом, расстояние
от точки М
до прямой
.
Таким
образом, расстояние
от точки М
до прямой ![]() равно
равно ![]() .
.
у 6
Задача. В параллелограмма ABCD точка К – середина стороны ВС, а точка М – середина стороны CD. Найдите AD, если АК = 6, АМ = 3, угол КАМ = 60°.
Решение.
В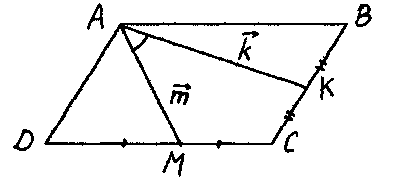 качестве базиса
выберем векторы
качестве базиса
выберем векторы
![]() и
и ![]() и составим
таблицу умножения
для векторов
этого базиса.
и составим
таблицу умножения
для векторов
этого базиса.
| * | k | m |
| k | 36 | 9 |
| m | 9 | 9 |
По формуле треугольника ![]() и
и ![]() .
.
Так как X – середина ВС, М – середина CD, то ![]() и
и ![]() , и получаем систему:
, и получаем систему:
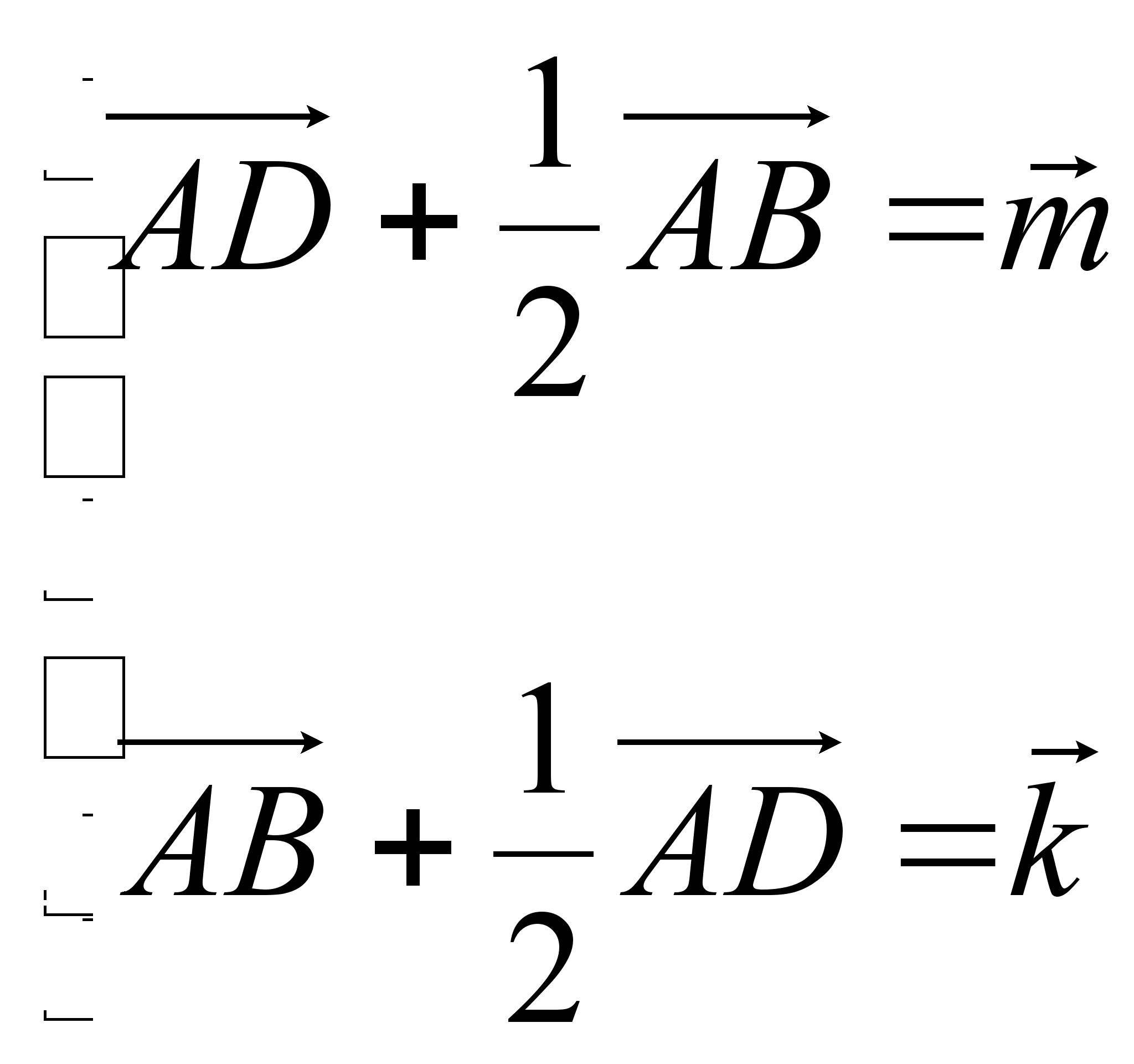
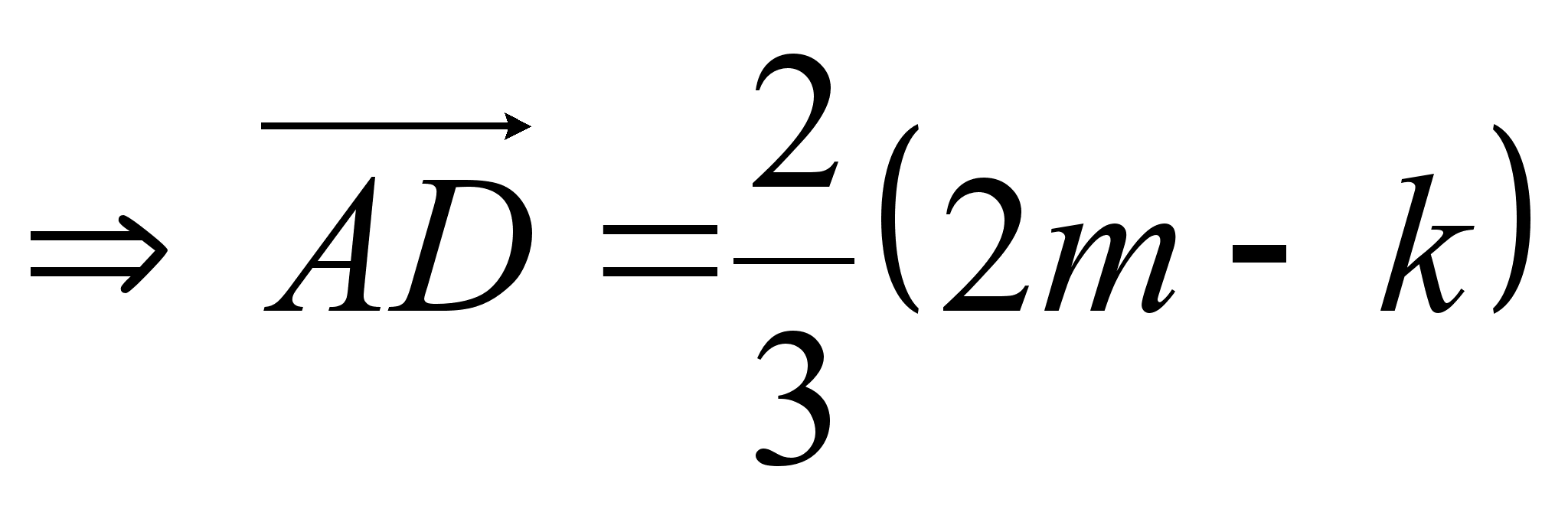 , откуда
, откуда
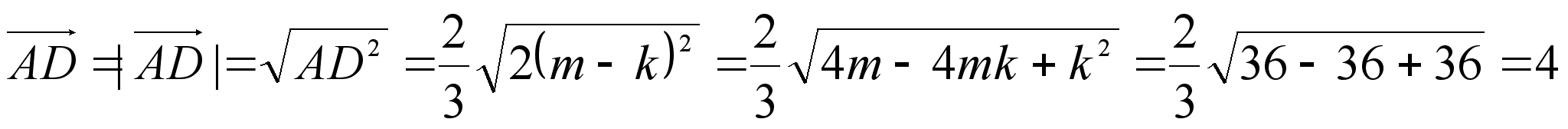
Ответ: 4.
Задача. Ребра СА, СВ, СС, треугольной призмы ABCA1В1С1 равны, соответственно 2, 3 и 4 образуют между собой углы ![]() ACB = 90°,
ACB = 90°, ![]() ACС1 = 45° и
ACС1 = 45° и ![]() BCC1 = 60°. Найдите объём призмы.
BCC1 = 60°. Найдите объём призмы.
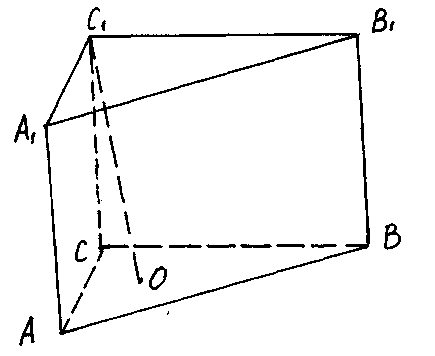
Пусть
отрезок С1О
является высотой
данной призмы.
Тогда ![]()
Для того, чтобы найти высоту С1О, выберем в качестве базиса векторы
![]() и составим
и составим
таблицу умножения.
| * | | | |
| | 4 | 0 | |
| | 0 | 9 | 6 |
| | | 6 | 16 |
Разложим
вектор C1O
по векторам
![]() .
Получим:
.
Получим:
![]() ,
где
,
где ![]() ,
а
,
а ![]() .
.
Таким
образом ![]() .
.
Коэффициенты
х,
у
находим из
условий перпендикулярности
вектора C1O
с векторами
![]() .
.
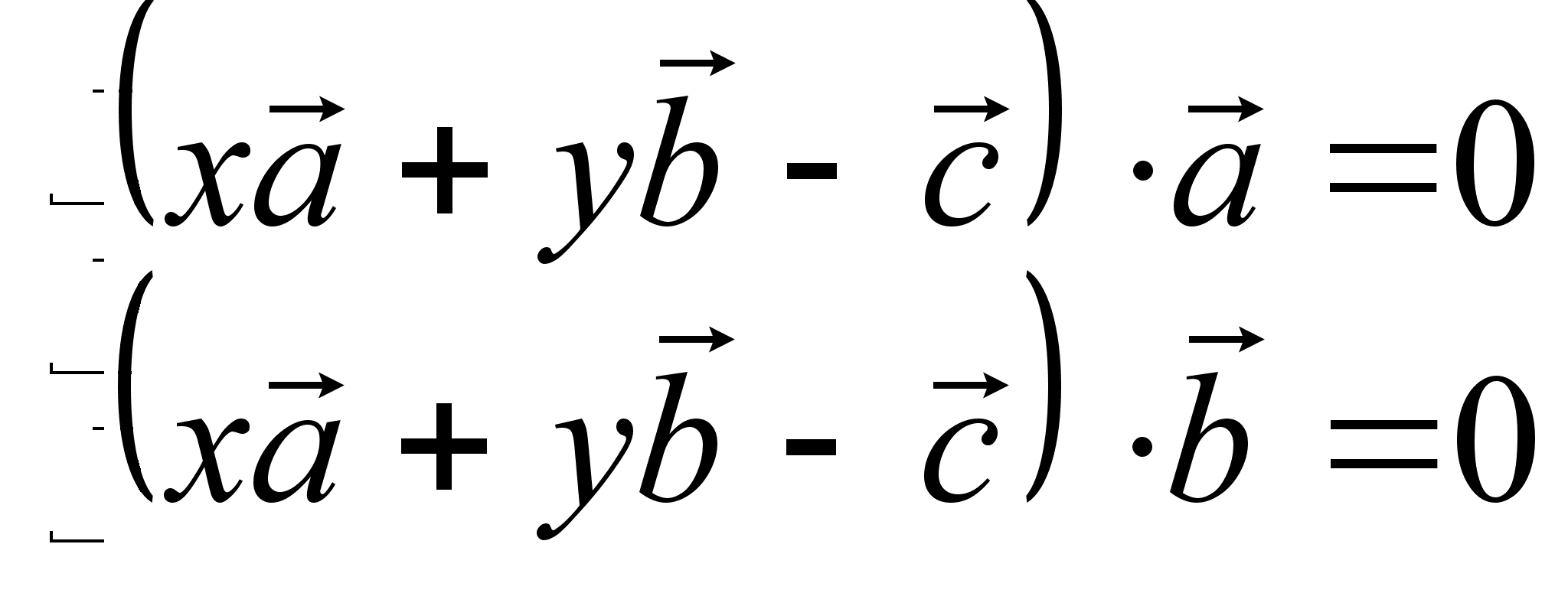
![]()
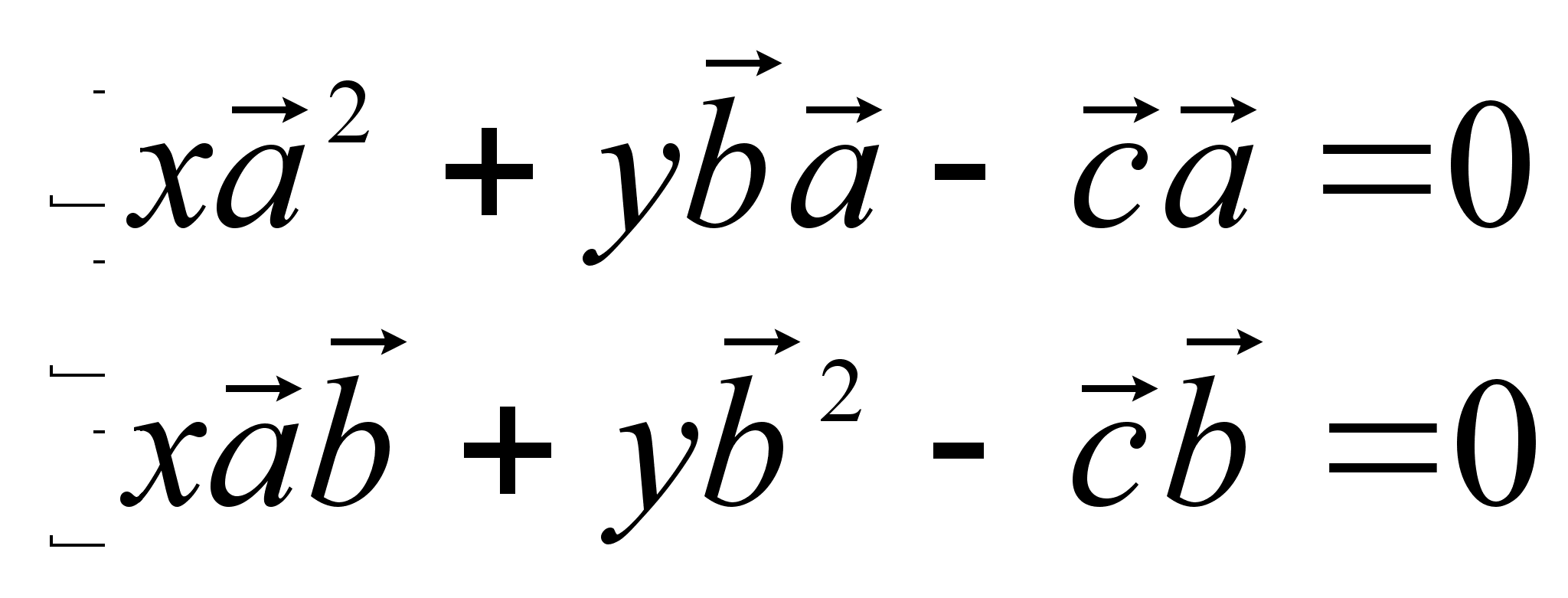
![]()
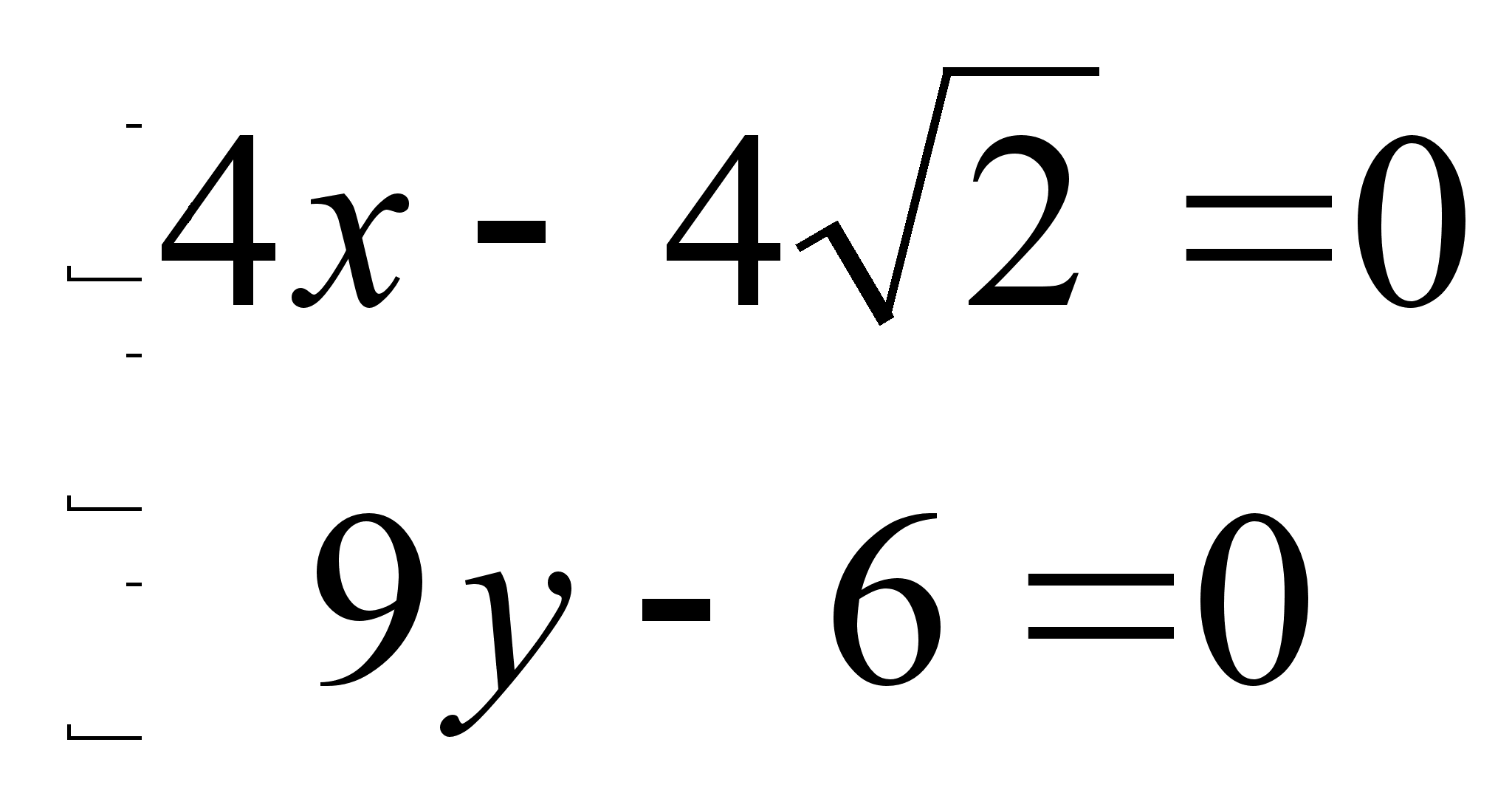
![]()
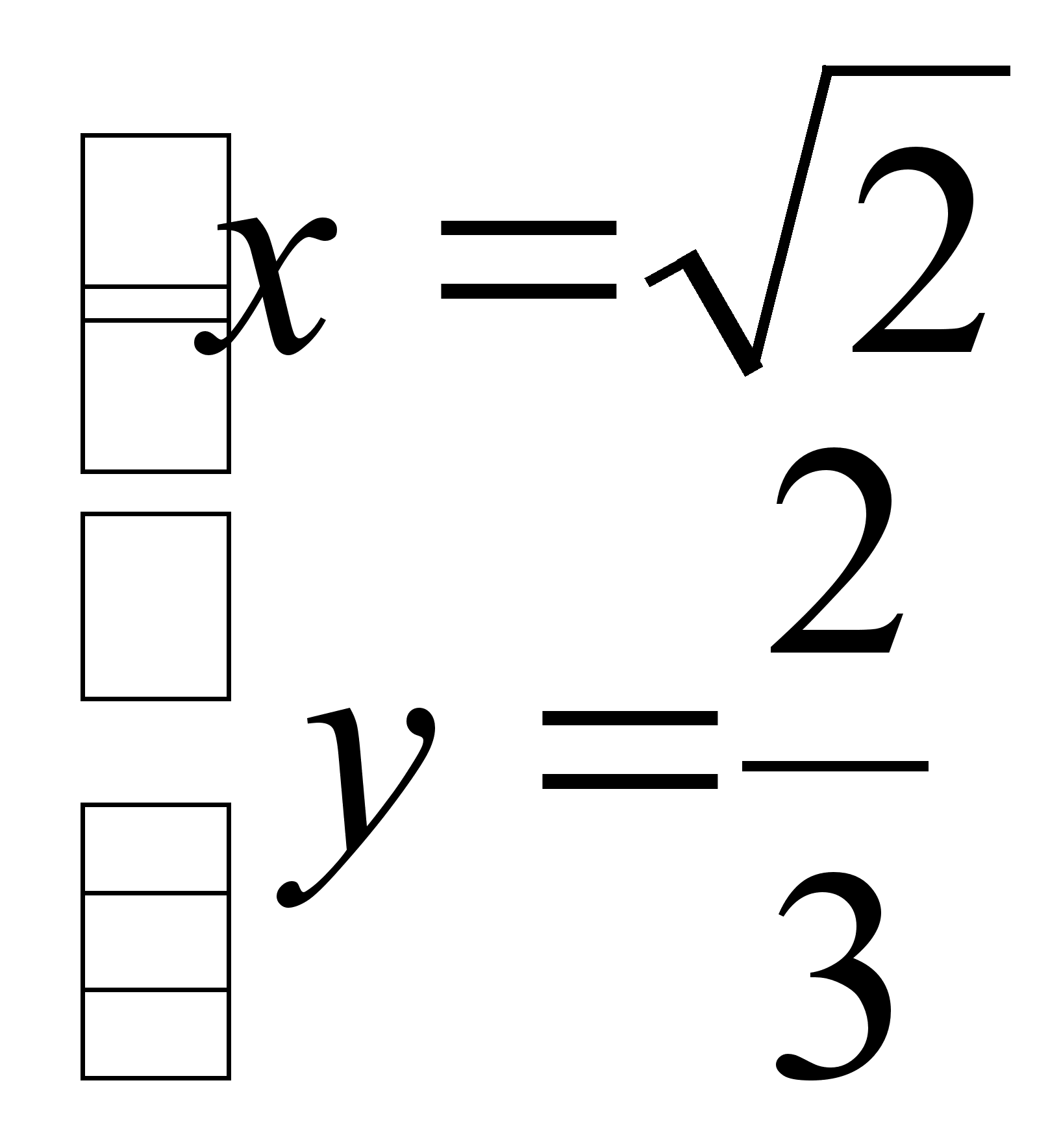 .
.
Следовательно,
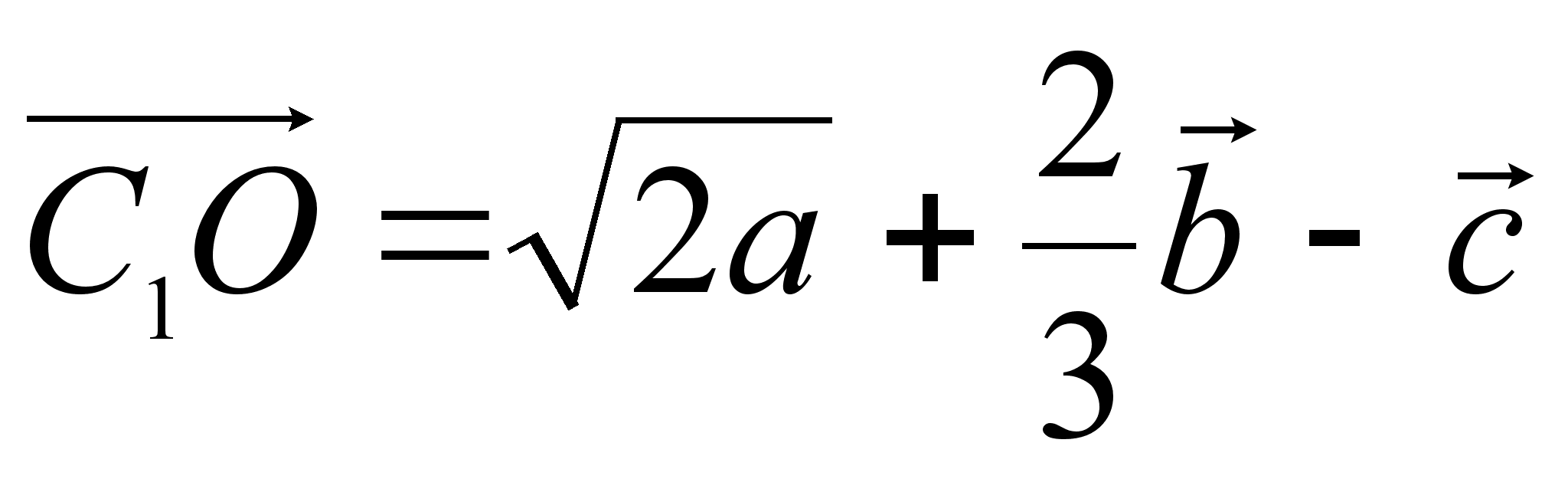
Значит
С1О
= 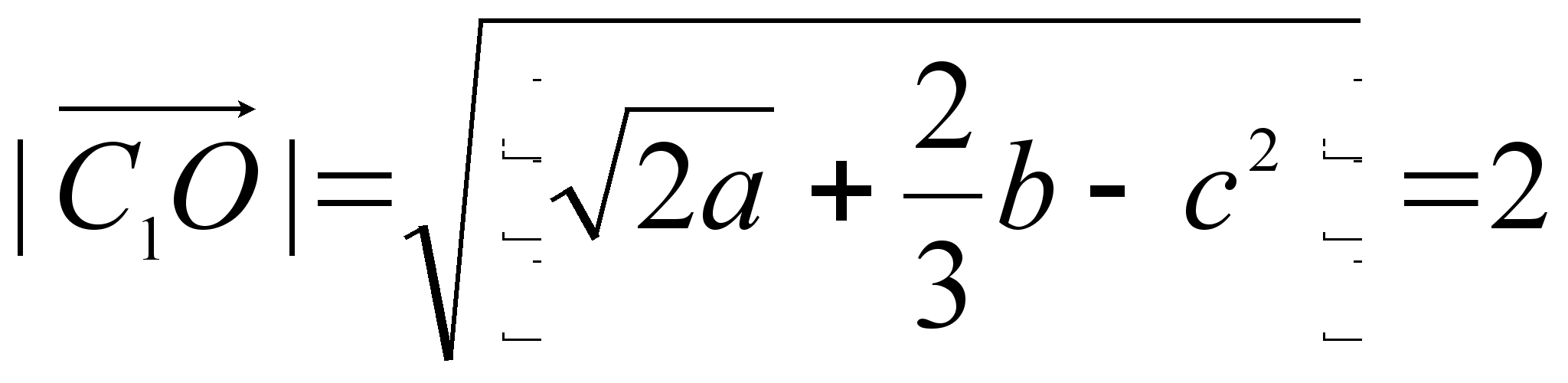
Тогда V = 3·C1O = 3·2 = 6
Ответ: 6.
С помощью векторов можно решать не только геометрические задачи, но и доказывать алгебраические неравенства.
I.
Доказать неравенство
![]()
Доказательство:
Рассмотрим
векторы ![]() и
и ![]() .
.
Их
скалярное
произведение
![]()
Так
как ![]() ,
,
![]() ,
то, учитывая
неравенство
,
то, учитывая
неравенство
![]() ,
получим
,
получим ![]() .
.
II. Докажем, что для любых неотрицательных чисел a, b, c справедливо неравенство:
![]()
Доказательство:
Рассмотрим векторы
![]() .
.
Глава 1
§1. Аксиоматика векторного пространства
Характеризация векторного пространства, как математической структуры осуществляются рядом аксиом.
Основные понятия теории: "вектор", "сумма двух векторов", "произведение вектора на действительное число".
Косвенным определением основных понятий теории векторного пространства являются следующие аксиомы:
I.
Для любых векторов
![]() и
и ![]() существует
единственный
третий вектор
существует
единственный
третий вектор
![]() ,
называемый
их суммой
,
называемый
их суммой
![]()
Таким образом аксиома I постулирует:
а) единственность этой суммы.
б)
существование
суммы двух
векторов ![]() и
и ![]() ;
;
Данная аксиома вводит на множестве векторов V операцию
f1: V x V V.
которая называется сложением двух векторов.
II. Сложение векторов коммутативно, т.е.
![]() .
.
III. Сложение векторов ассоциативно, т.е.
![]()
![]()
IV.
Существует
вектор ![]() такой, что
такой, что ![]() для любого
вектора,
для любого
вектора, ![]() т.е.
т.е.
![]()
![]()
Определение
1.1. Вектор
![]() ,
удовлетворяющий
аксиоме IV,
называется
нулевым вектором
и обозначается
,
удовлетворяющий
аксиоме IV,
называется
нулевым вектором
и обозначается
![]()
V.
Для каждого
вектора ![]() существует
такой вектор
существует
такой вектор
![]() ,
что
,
что ![]() +
+![]() =
=![]()
![]()
![]()
Определение
1.2. Вектор
![]() ,
удовлетворяющий
аксиоме V,
называется
противоположным
вектору
,
удовлетворяющий
аксиоме V,
называется
противоположным
вектору ![]() .
.
VI.
Для любого
вектора ![]() и действительно
числа
и действительно
числа ![]() ,
существует
единственный
вектор
,
существует
единственный
вектор ![]() ,
называемый
произведением
вектора
,
называемый
произведением
вектора ![]() на число
на число ![]() и обозначаемый
т.о.:
и обозначаемый
т.о.: ![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
,
![]()
Данная аксиома вводит операция нового типа (внешнюю операцию):
![]()
Эта операция носит название «умножение вектора на число».
VII.
Для любого
вектора ![]() умножение
вектора
умножение
вектора ![]() на 1 не изменяет
вектора
на 1 не изменяет
вектора ![]() ,
т.е.
,
т.е.
![]() ,
,
![]()
VIII. Умножение вектора на число ассоциативно, т.е.
![]() ,
,
![]() ,
,
![]()
IX. Умножение вектора на число дистрибутивно сложения чисел, т.е.
![]() ,
,
![]() ,
,
![]()
X. Умножение вектора на число дистрибутивно относительно сложения векторов, т.е.
![]() ,
,
![]() ,
,
![]()
Этим заканчивается аксиоматика векторного пространства, которое можно теперь определить т.о.:
множество V с введенными двумя операциями
![]()
![]() ,
,
подчиняющееся аксиомам I-X, называется векторным пространством над полем действительных чисел R.
§2. Следствие из аксиом векторного пространства
Из аксиом I-X можно вывести целый ряд предложений.
Теорема 2.1. Существует единственный нулевой вектор.
Доказательство:
Предложим,
что существует
два различных
вектора ![]() и
и ![]() таких, что
таких, что ![]() и
и ![]() для любого
вектора
для любого
вектора ![]() .
.
Положим
![]() .
Тогда
.
Тогда
![]() и
и
![]() (1)
(1)
Положим
теперь ![]() .
Аналогично
получим:
.
Аналогично
получим:
![]() и
и
![]() (2)
(2)
Так
как ![]() (по аксиоме
II),
то из (1) и (2) следует,
что
(по аксиоме
II),
то из (1) и (2) следует,
что ![]() .
.
Таким
образом, векторное
пространство
содержит единственный
вектор ![]() ,
удовлетворяющий
равенству
,
удовлетворяющий
равенству ![]() .
.
Теорема
2.2. Для
любого вектора
![]() существует
единственный
противоположный
вектор
существует
единственный
противоположный
вектор ![]() .
.
Или:
![]() и
и ![]()
Доказательство:
Допустим,
что ![]() и
и ![]() и
и ![]() ,
т.е. существует
,
т.е. существует
![]() ,
имеющий два
различных
противоположных
вектора
,
имеющий два
различных
противоположных
вектора ![]() и
и ![]() .
.
![]() и (1)
и (1)
![]() (2)
(2)
Тогда
![]() и
и
![]() (3)
(3)
Левые части равенств (3) равны между собой. Действительно:
![]() (4)
(4)
Из
равенства (3) и
(4) следует, что
![]() .
.
Теорема
2.3.
Для
любых векторов
![]() и
и ![]() существует
единственный
вектор
существует
единственный
вектор ![]() ,
такой, что
,
такой, что ![]() .
.
Доказательство:
I.
Существование.
Убедимся, что
в качестве
вектора ![]() можно будет
выбрать вектор
можно будет
выбрать вектор
![]() .
В самом деле,
.
В самом деле,
![]()
Таким
образом, для
векторов ![]() и
и ![]() существует
вектор
существует
вектор ![]() ,
удовлетворяющий
равенству:
,
удовлетворяющий
равенству:
![]() .
.
II. Единственность (от противного). Пусть
![]() и
и
![]() (1)
(1)
Тогда:
![]()
Отсюда
![]() .
Получим противоречие
с допущением.
Таким образом,
единственность
вектора
.
Получим противоречие
с допущением.
Таким образом,
единственность
вектора ![]() доказана.
доказана.
Определение
2.1.
Вектор![]() ,
удовлетворяющий
равенству
,
удовлетворяющий
равенству ![]() ,
называется
разностью
векторов
,
называется
разностью
векторов ![]() и
и ![]() ,
и обозначается
через
,
и обозначается
через ![]() -
-
![]() .
.
Таким образом
![]()
Теорема 2.3., как видно, вводит на множестве v новую операцию "–":
![]()
называемую вычитанием, которая является обратной по отношению к операции сложения.
Следствие
1. ![]()
Теорема
2.4. ![]()
Доказательство:
![]() ,
т.к.
,
т.к. ![]() - вектор, противоположный
вектору
- вектор, противоположный
вектору ![]() .
Тогда
.
Тогда
![]() Ч.т.д.
Ч.т.д.
Теорема
2.5. ![]()
Доказательство:
Имеем:
![]() ;
;
![]()
Отсюда следует,
что ![]() .
.
Ч.т.д.
Теорема
2.6. ![]() .
.
Доказательство:
Имеем:
![]()
![]()
Отсюда следует,
что ![]() .
.
Теорема
2.7.
![]()
Доказательство:
Имеем:
![]() (по
Теореме 2.6.)
(по
Теореме 2.6.)
Отсюда следует,
что ![]() .
.
Следствие
2. ![]() .
.
Теорема
2.8. ![]() или
или ![]() .
.
Доказательство:
Возможны два случая:
I. ![]() и
и
II. ![]() .
.
I. Если ![]() ,
то дизъюнкция
,
то дизъюнкция ![]() или
или ![]() истинна и теорема
доказана.
истинна и теорема
доказана.
II. Пусть ![]() .
Тогда существует
число
.
Тогда существует
число ![]() ,
отсюда имеем:
,
отсюда имеем:
![]() (по условию Т.
2.5.)
(по условию Т.
2.5.) 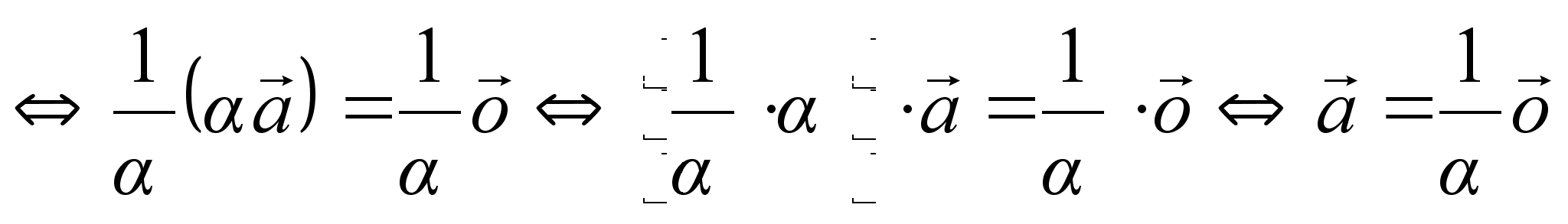 ,
,
(по Т. 2.5.) ![]() .
.
Таким образом,
в случае II
имеем, что ![]() .
.
Итак, если
![]() ,
то
,
то ![]() или
или ![]() .
.
Теорема
2.9. ![]() .
.
Доказательство:
Для того,
чтобы установить,
что вектор ![]() является
противоположным
для вектора
является
противоположным
для вектора
![]() ,
необходимо
и достаточно
проверить,
выполняется
ли следующее
равенство:
,
необходимо
и достаточно
проверить,
выполняется
ли следующее
равенство:
![]() ,
или все равно,
что
,
или все равно,
что ![]() .
.
Имеем:
![]()
Таким образом
![]() или
или ![]() .
И, следовательно,
.
И, следовательно,
![]() .
.
Рассмотренные свойства операций над векторами аналогичны соответствующим свойствам арифметических операций над числом. Так, например, сумма конечного числа векторов, как и сумма в любой коммуникативной группе, не зависит ни от порядка слагаемых в этой сумме, ни от способа расстановки скобок:
![]() и т.д.
и т.д.
Однако между
векторной и
числовой алгеброй
существуют
серьезные
отличия. Одно
из наиболее
существенных
отличий состоит
в том, что множество
векторов не
является
упорядоченным,
т.е. для векторов
нельзя ввести
отношение
«меньше» и
«больше». Например
для двух противоположных
чисел ![]() и
и ![]() мы знаем, что
мы знаем, что
![]() и, что одно из
этих двух чисел
больше 0, а другое
– меньше 0. Для
векторов же,
удовлетворяющих
равенству
и, что одно из
этих двух чисел
больше 0, а другое
– меньше 0. Для
векторов же,
удовлетворяющих
равенству ![]() ,
постановка
вопроса о том,
какой из векторов
,
постановка
вопроса о том,
какой из векторов
![]() или
или ![]() больше нулевого,
а какой меньше
нулевого,
бессмысленна.
больше нулевого,
а какой меньше
нулевого,
бессмысленна.
§3. Размерность
Определение 3.1. Векторное пространство называется n-мерным, если в нем имеется n линейно независимых векторов, а всякие n+1 векторы линейно зависимы.
Иначе говоря, размерность векторного пространства – это максимальное число содержащихся в нем линейно независимых векторов.
Если максимальное число линейно независимых векторов равно 1, то векторное пространство называется одномерным, если это число равно 2,. То векторное пространство называется двумерным, и т.д.
Векторное пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором существует сколь угодно линейно независимых векторов, называется бесконечномерным.
Определение 3.2. Совокупность n линейно независимых векторов n-мерного векторного пространства называется его базой.
Теорема
3.1.
Каждый
вектор ![]() n-мерного
векторного
пространства
можно представить,
и притом единственным
образом, в виде
линейной комбинации
векторов базы.
n-мерного
векторного
пространства
можно представить,
и притом единственным
образом, в виде
линейной комбинации
векторов базы.
Доказательство:
Пусть
![]() – произвольная
база n-мерного
векторного
пространства.
Так как любые
n+1
векторы n-мерного
векторного
пространства
линейно зависимы,
то векторы
– произвольная
база n-мерного
векторного
пространства.
Так как любые
n+1
векторы n-мерного
векторного
пространства
линейно зависимы,
то векторы
![]() ,
,
линейно
зависимы, т.е.
нулевой вектор
является
нетривиальной
линейной комбинацией
векторов ![]() :
:
![]() ,
,
где
![]() не все равны
нулю. При этом
не все равны
нулю. При этом
![]() .
Если бы
.
Если бы ![]() ,
то тогда среди
чисел
,
то тогда среди
чисел ![]() хотя бы одно
было отлично
от нуля, а отсюда
следует, что
векторы
хотя бы одно
было отлично
от нуля, а отсюда
следует, что
векторы ![]() линейно зависимы.
линейно зависимы.
Пусть
например, ![]() ,
тогда
,
тогда 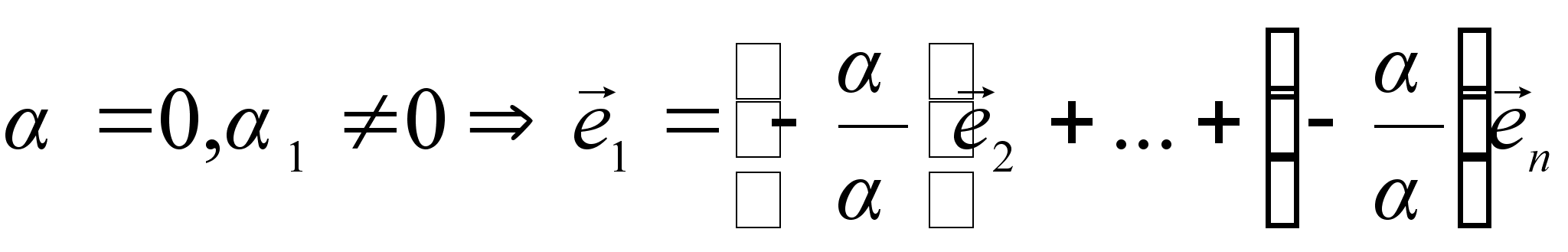 .
.
Откуда
следует линейная
зависимость
векторов ![]() ,
что противоречит
условию.
,
что противоречит
условию.
Итак,
![]() .
Если
.
Если ![]() ,
то
,
то
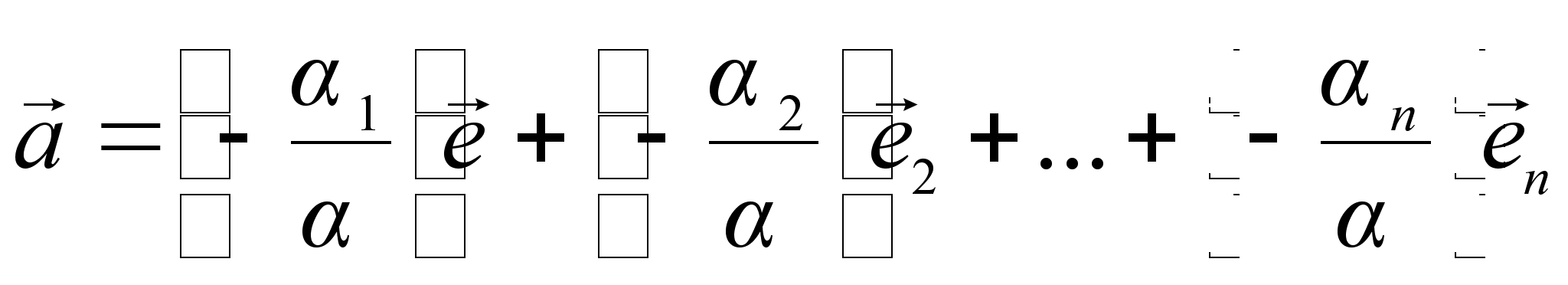
Полученное
представление
вектора ![]() является искомым.
является искомым.
Докажем, что оно единственно.
Допустим,
что возможны
два представления
вектора ![]() в виде линейной
комбинации
базы:
в виде линейной
комбинации
базы:
![]() и
и
![]() .
.
Тогда
![]() ,
отсюда
,
отсюда
![]() .
.
Так
как векторы
![]() линейно независимы,
то
линейно независимы,
то
![]()
и, следовательно,
![]() .
.
Ч.т.д.
Примеры.
Похожие работы
... , т. е. такие пары точек считаются за одну точку. Из этого определения следует, что при возрастании n число типов неевклидовых пространств также растет. Неевклидовы геометрии являются геометриями простейших римановых пространств определенной и неопределенной метрики, составляющих так называемый класс пространств постоянной ненулевой кривизны. Каждое из таких n-мерных пространств допускает ...
... , СССР; Том, С. П. Новиков) и теория сглаживания и триангулируемости (Дж. Милнор, США). Развитие Т. продолжается во всех направлениях, а сфера её приложений непрерывно расширяется. Определение топологического пространства Напомним классическое определение непрерывности числовой функции f в точке x, восходящее к Коши. Определение 1. Функция f называется непрерывной в точке x, если для любого e ...
... объём Vk шара радиуса r в k-пространстве при чётном и нечётном n соответственно равен , (9. 12) Формула (9. 12) дает при k = 2, 3, 4, 5 соответственно , , , (9. 13) Глава III. Применения многомерной геометрии § 10. О необходимости введения многомерного пространства (на примерах задач) В чём состоит польза многомерных пространств? Где они применяются? Зачем понадобилось ...
... А3, А4, А5, А6 называемых вершинами и шести прямых А1А2, А2А3, А3А4, А4А5, А5А6, А6А1 называемых сторонами. Мы рассмотрели один из подходов к определению проективной плоскости, а именно определения проективной плоскости на базе трехмерного векторного пространства. Теперь рассмотрим аналитическое определение проективной плоскости. Глава 2. Аналитическое построение проективной плоскости. 2.1. ...
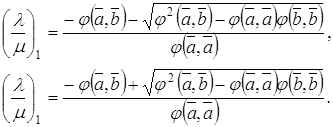
0 комментариев