Определим размерность векторного пространства геометрических векторов трехмерного пространства

1. Определим размерность векторного пространства геометрических векторов трехмерного пространства.

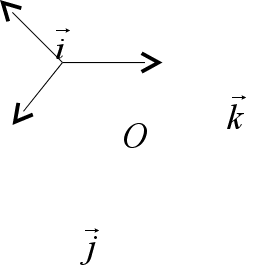
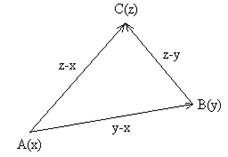
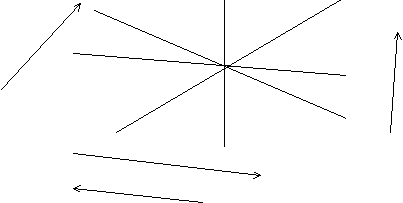
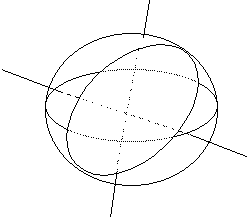
Докажем, что любые три вектора выходящие из одной точки О и не лежащие в одной плоскости, являются линейно независимыми, а всякие четыре вектора линейно зависимы.

В самом деле, векторы независимы, т.к. в противном случае один из них, например , должен был бы линейно выражаться через два других. Однако равенство : вектор является диагональю параллелограмма, построенного на векторах и . Отсюда векторы и и – компланарны, что противоречит условию их выбора.

Докажем теперь, что любые четыре вектора – линейно зависимы.

Возможны следующие случаи.

а) Векторы компланарны, тогда любая тройка векторов линейно зависима. Если система имеет подсистему линейно зависимых векторов, то эта система линейно зависима.

б) Из четырех векторов существует три компланарных, а следовательно, три линейно зависимых вектора. Как и выше, вся система векторов будет линейно зависимой.

в) Из четырех данных векторов никакие три не являются компланарными. В этом случае никакие три, а следовательно, и никакие два вектора из числа данных не являются линейно зависимыми.

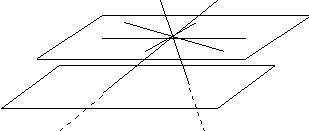
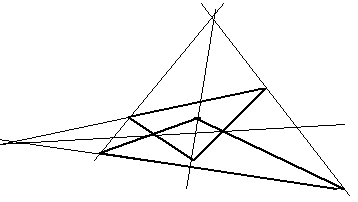
П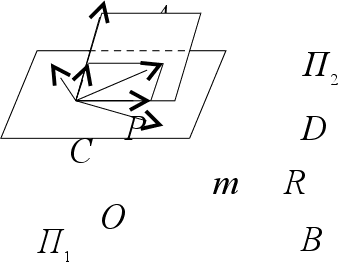усть .

Обозначим плоскость (OBC) через П₁, а плоскость (AOD) через П₂.

(Такие плоскости существуют, так как пара векторов и и пара векторов и - пары линейно независимых векторов). Плоскости П₁ и П₂ имеют общую точку О. Тогда эти плоскости имеют общую прямую m, проходящую через эту точку О.

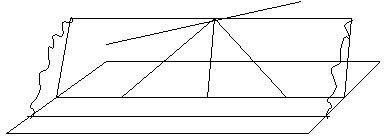
В плоскости П₂ построим параллелограмм OPDR с диагональю OD. Тогда , где . Вектор , лежащий в плоскости П₁ является линейной комбинацией векторов и : . Тогда , или . Отсюда, по теореме 5.1., векторы линейно независимы.

Итак, множество геометрических векторов трехмерного евклидового пространства представляет собой трехмерное векторное пространство.

2. Пространство арифметических векторов длины n представляет собой n-мерное векторное пространство.

Докажем это.

Прежде всего, нетрудно установить существование n линейно независимых векторов. Возьмем векторы:

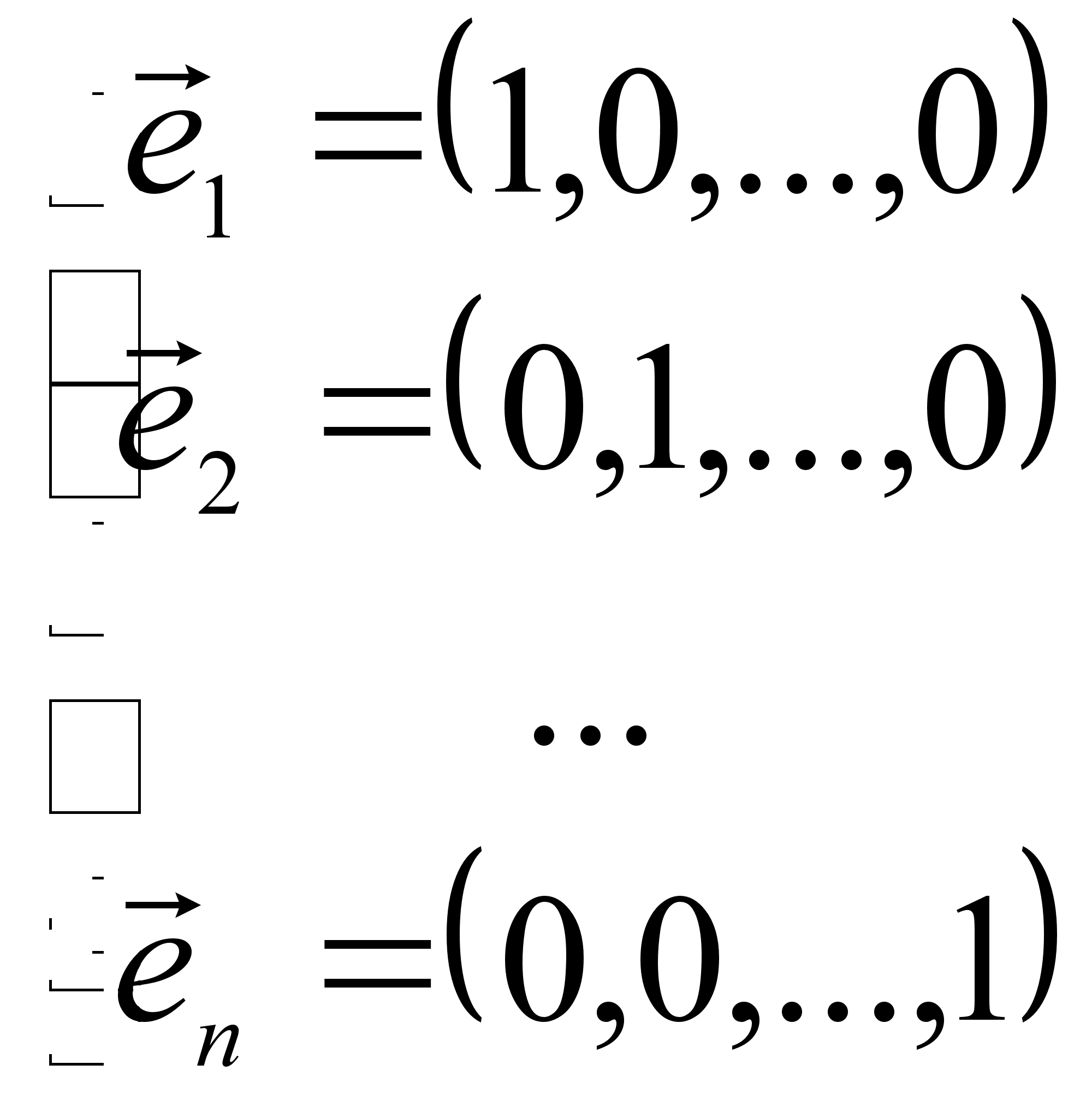
и докажем, что они линейно независимы. В самом деле, если допустить, что эти векторы линейно зависимы, тогда на основании теоремы 5.1. хотя бы один из них есть линейная комбинация остальных. Пусть, например, есть линейная комбинация остальных:

(1)

тогда

.

Отсюда

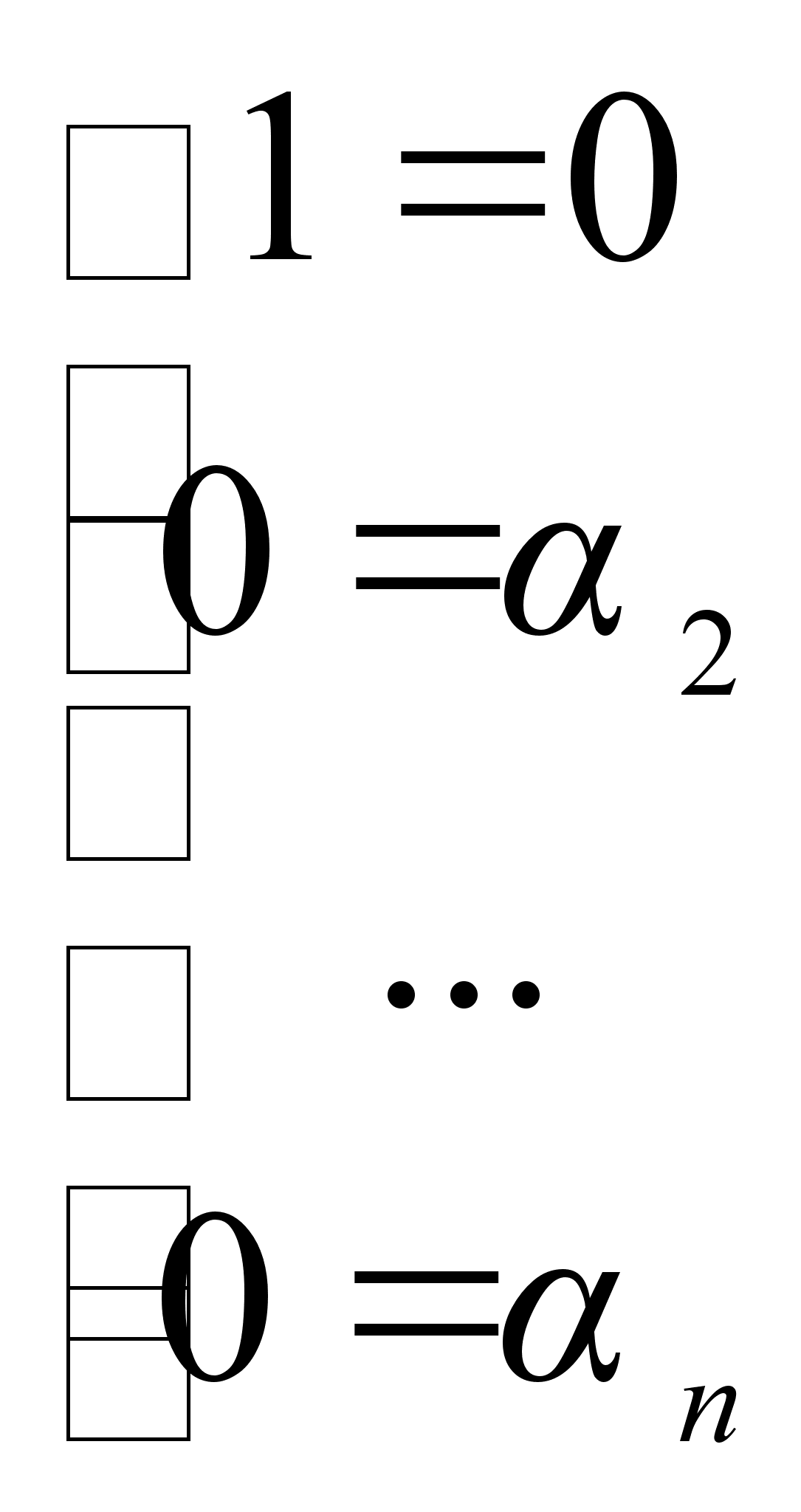(2)

Система (2) является несовместной. Следовательно, не существует такого выбора коэффициентов , чтобы равенство (1) удовлетворялось. Таким образом, линейная независимость системы векторов доказана.

Докажем теперь, что всякие n+1 арифметические вектора линейно зависимы. Пусть имеется система из n+1 векторов:

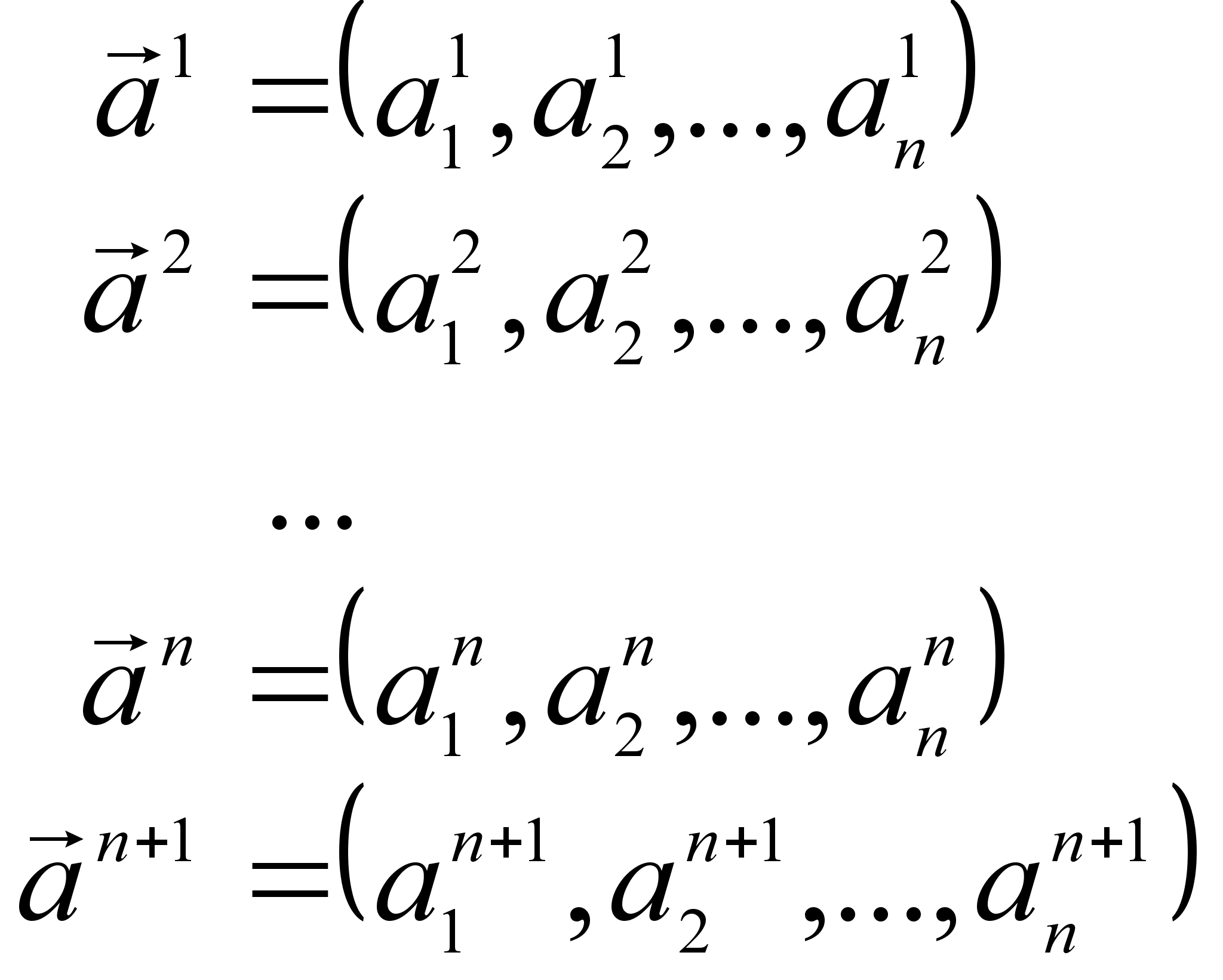
Выясним, существуют ли числа , не все равны нулю, такие, что

(3)

Равенство (3) эквивалентно системе:

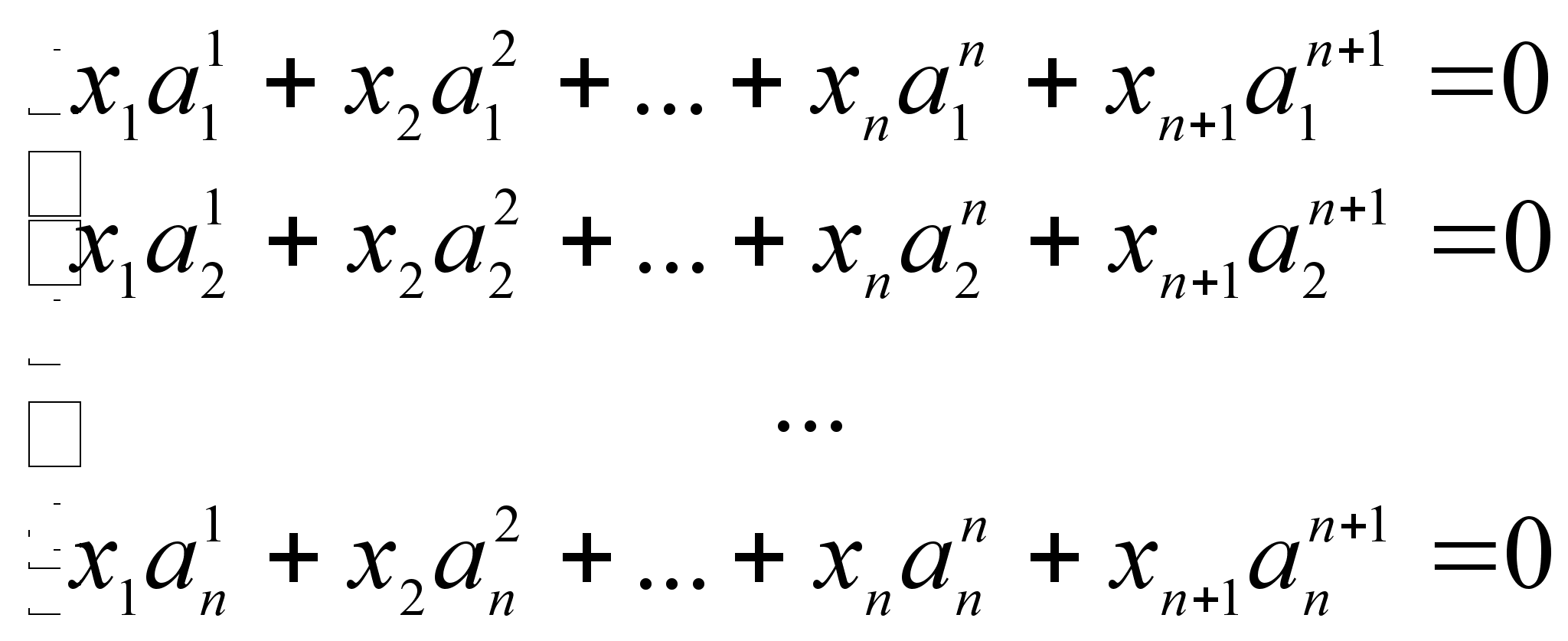(4)

Получим систему однородных уравнений, в которых число уравнений n, а число неизвестных m=n+1. Такая система всегда имеет ненулевое решение и, следовательно, система векторов является линейно зависимой.

Контрпример. Рассмотрим совокупность всех непрерывных функций на сегменте [0; 1]. Нетрудно убедиться, что в данном случае мы имеем дело с векторным пространством над полем действительных чисел R. Пусть n – произвольное натуральное число.

Положим:

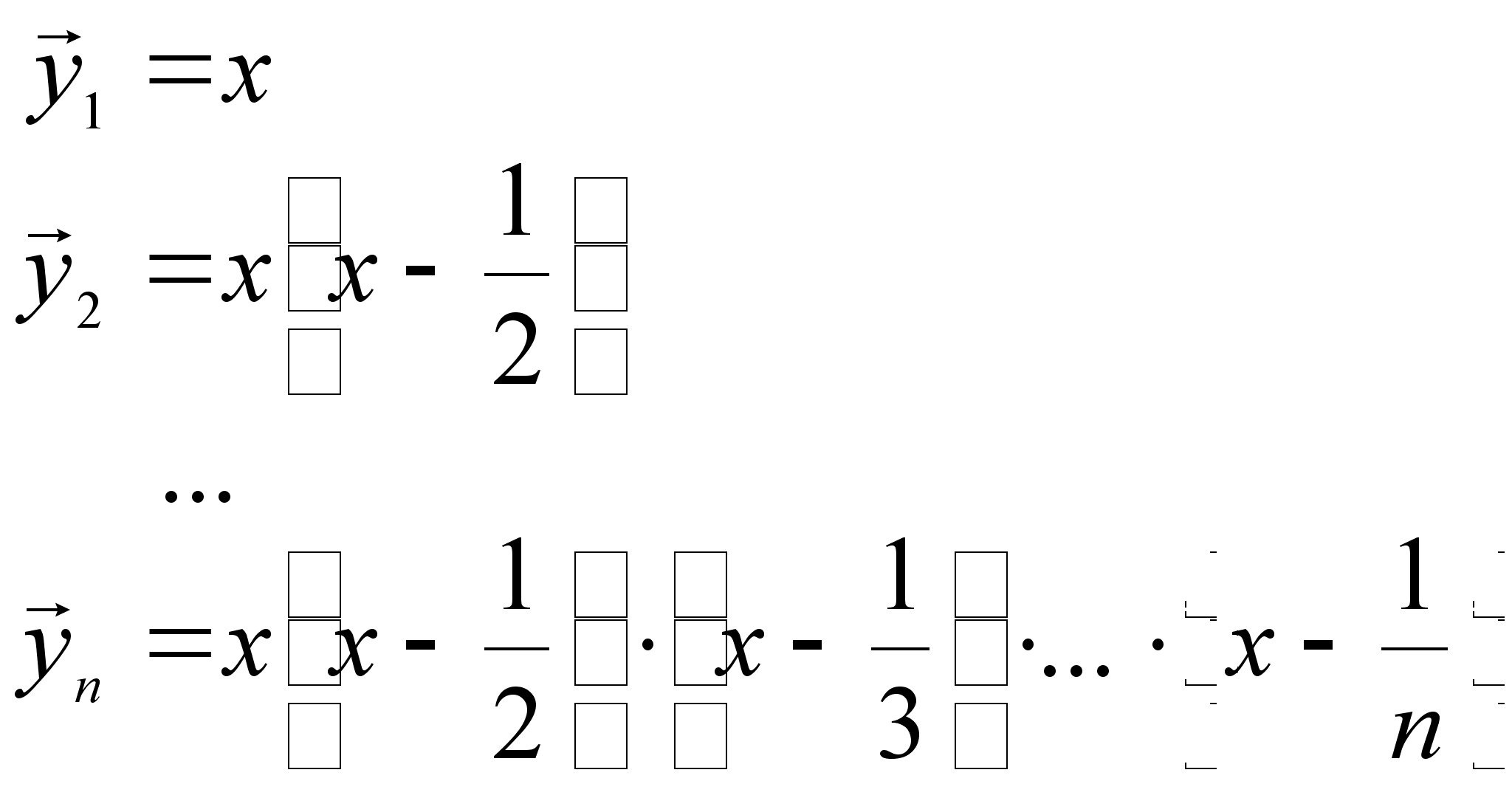
Докажем, что система векторов является линейно независимой. Запишем равенство.

.

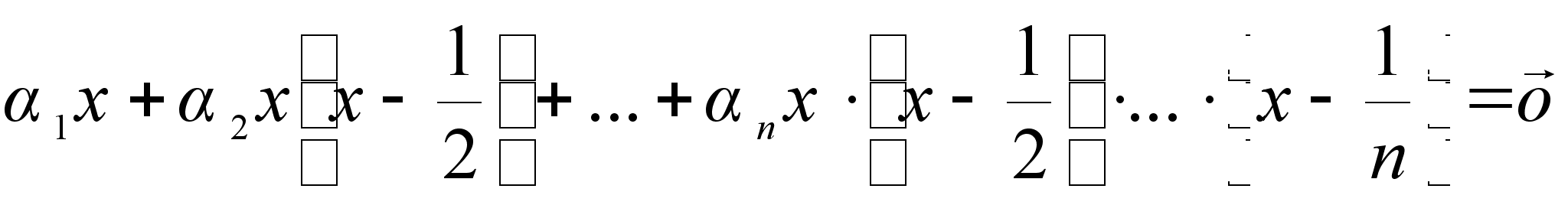Положив последовательно 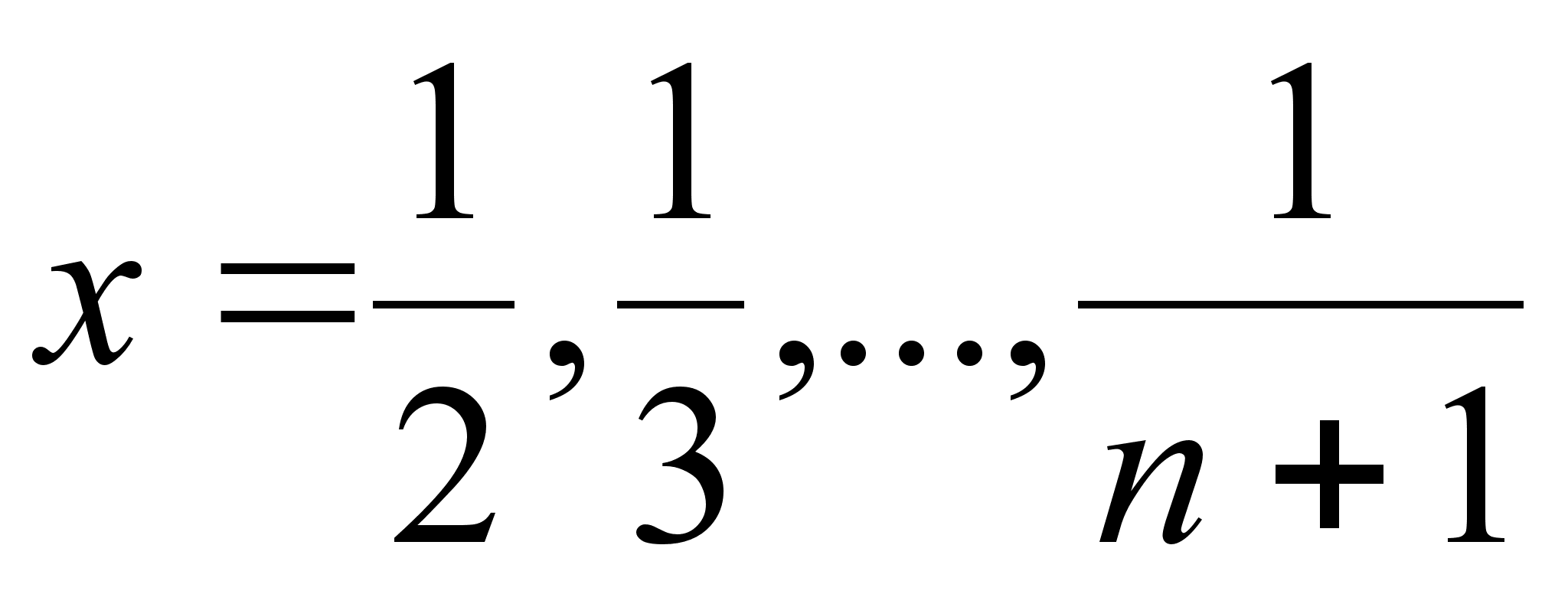, , получим

Таким образом, равенство

влечет за собой равенство

Отсюда, векторы линейно независимы. Так как n – любое натуральное число, то, следовательно, векторное пространство всех непрерывных функций заданных на отрезке [0; 1] не имеет конечной системы линейно независимых векторов, для которых всякая система, содержащая на один больше векторов, была бы линейно зависима. Поэтому в этом пространстве нельзя ввести понятие конечной размерности. Такие пространства называются бесконечными.

§4. Аксиоматика Евклидово-векторного пространства

n-мерное векторное пространство называется евклидовым, если оно удовлетворяет дополнительной группе аксиом (называемыми аксиомами скалярного произведения). Эти аксиомы вводят в n-мерное векторное пространство новое понятие – понятие скалярного произведения двух векторов.

Аксиомы:

XII. Для любых двух векторов и существует единственное число , называемое их скалярным произведением.

Обозначение: - скалярное произведение векторов и .

Таким образом,

Аксиома XII утверждает по сути дела, существование отображения VxVR, ставшего в соответствие каждой паре векторов единственное число из R.

Это отображение называется скалярным умножением двух векторов.

XIII. Скалярное умножение двух векторов коммутативно:

XIV. Скалярное умножение ассоциативно относительно умножения вектора на число:

XV. Скалярное умножение диструбутивно относительно сложения векторов:

XVI. Для любого вектора и

Примеры.

1. рассмотрим трехмерное пространство геометрических векторов. Под скалярным произведением двух векторов и будем понимать число , где и длины векторов и соответственно, а  - угол между данными векторами.

Нетрудно установить, что, определив скалярное произведение таким образом, мы удовлетворим всем аксиомам скалярного произведения двух векторов. Следовательно, трехмерное пространство геометрических векторов с введенным таким образом скалярным произведением является евклидовым.

2. Рассмотрим трехмерное пространство арифметических векторов. Под скалярным произведением векторов (x₁;y₁;z₁) и (x₂;y₂;z₂) будем понимать число легко можно проверить, что аксиомы скалярного произведения двух векторов будут удовлетворены. Следовательно, трехмерное пространство арифметических векторов (с введенным таким образом скалярным произведением) является евклидовым.

3. Рассмотренный пример можно обобщить на n-мерное пространство арифметических векторов, если скалярное произведение двух векторов и .

Определить равенством (1)

Таким образом, n-мерное пространство арифметических векторов с введенным равенством (1) скалярным произведением, является евклидовым.

§5. Следствия из аксиом скалярного произведения

1.

Доказательство:

Имеем (1). Тогда

Определение 5.1. называется длиной вектора .

Обозначение: - длина вектора .

Таким образом, .

2. . Это вытекает из принятого определения и следствия 1.

3. , где - вектор, противоположный вектору .

Доказательство:

4. Для любых и имеет место неравенство Коши-Буняковского:

Доказательство.

Рассмотрим скалярное произведение вектора на себя.

Имеем:

(XVI)

где t – любое действительное число. Отсюда на основании аксиом XIII-XV получаем:

Выражение в левой части неравенства представляет собой квадратный трехчлен относительно t. Так как этот трехчлен должен быть неотрицательным при всех значениях t, то он не может иметь двух различных корней и, поэтому, его дискриминант:

Отсюда

Определение 5.2. Число 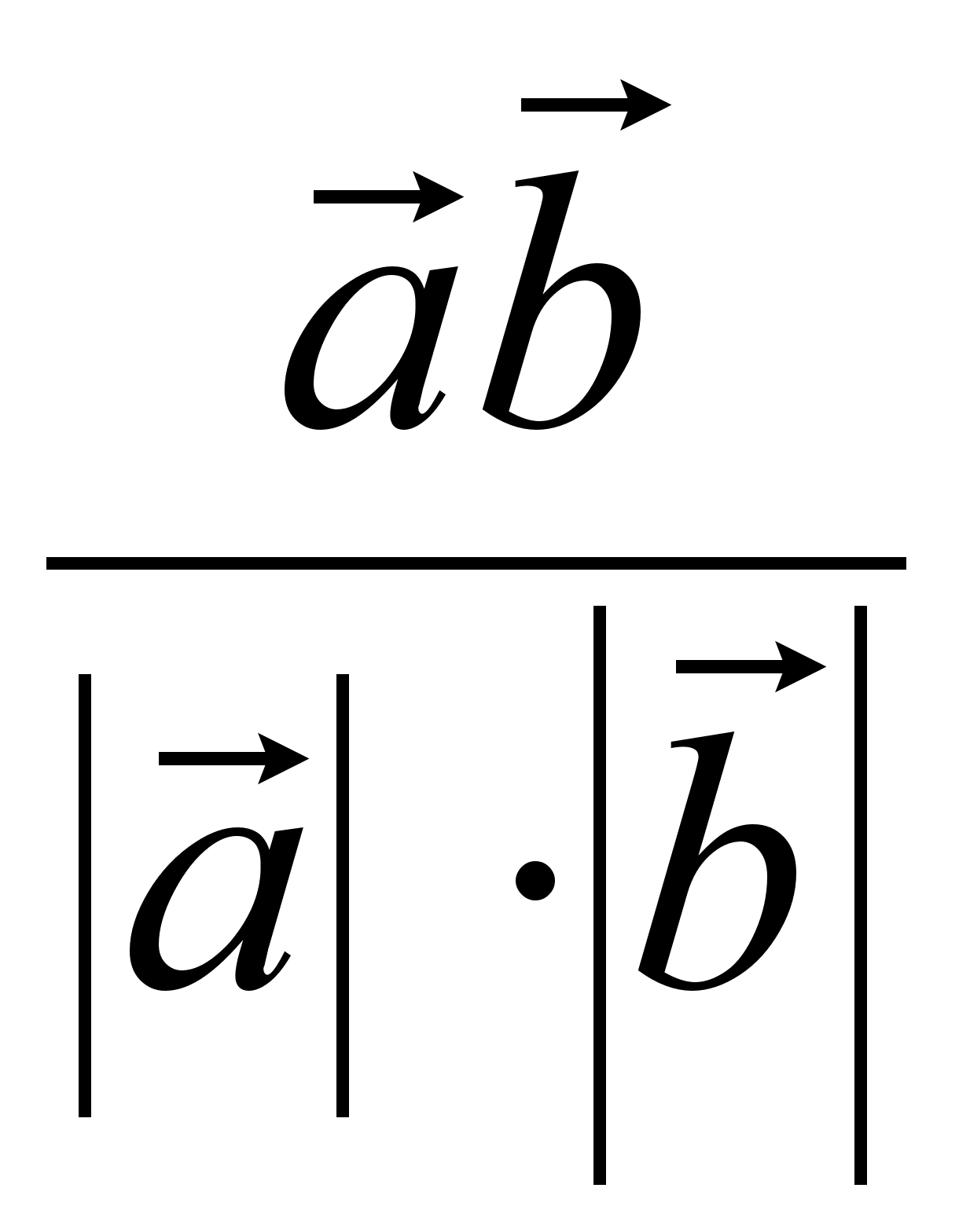называют косинусом угла между векторами и .

Итак,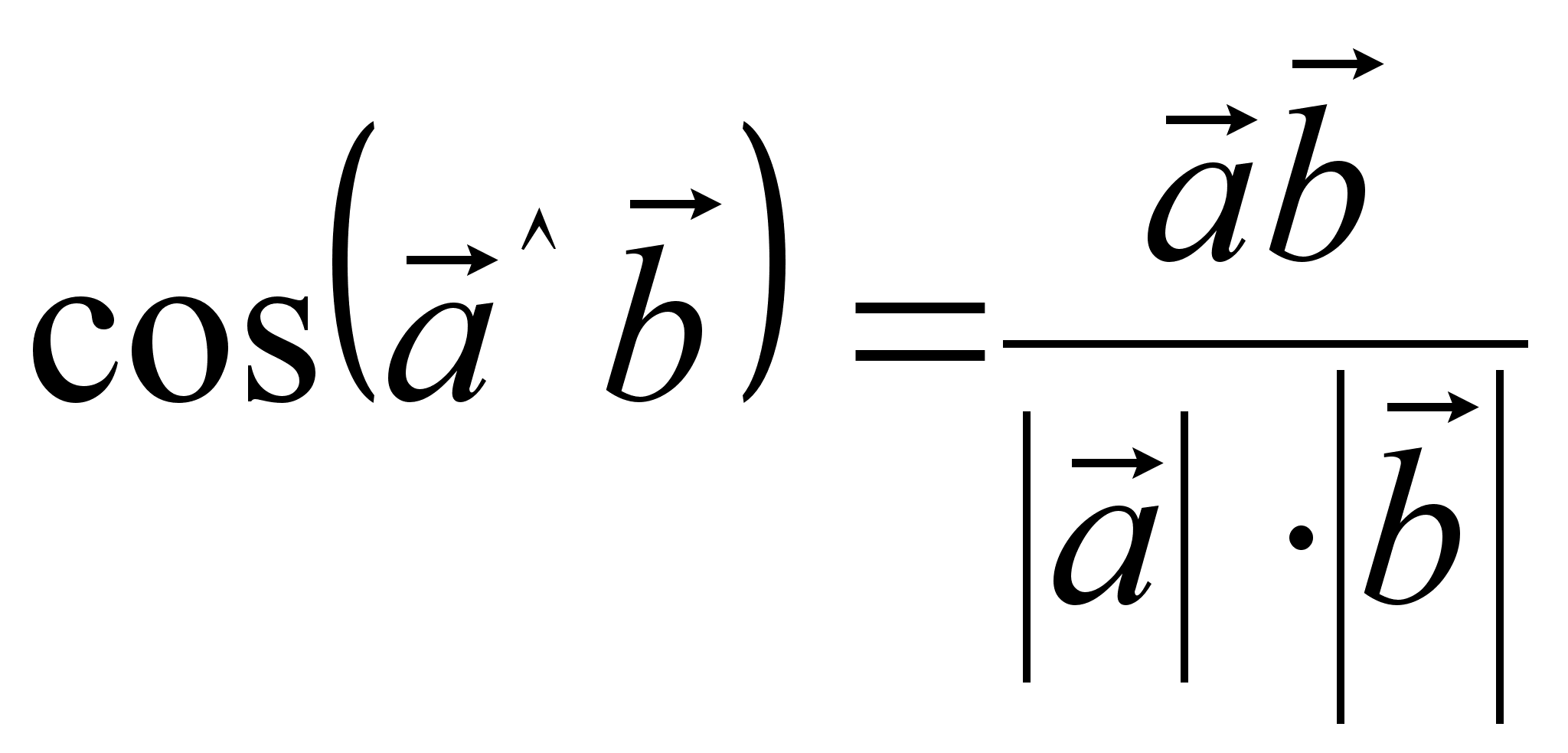

Введение такого определения оправдывается, в частности, следующими неравенствами:

Этот факт непосредственно следует из следствия 4.

5. (Неравенство треугольника)

Доказательство:

Воспользуемся неравенством Коши-Буняковского:

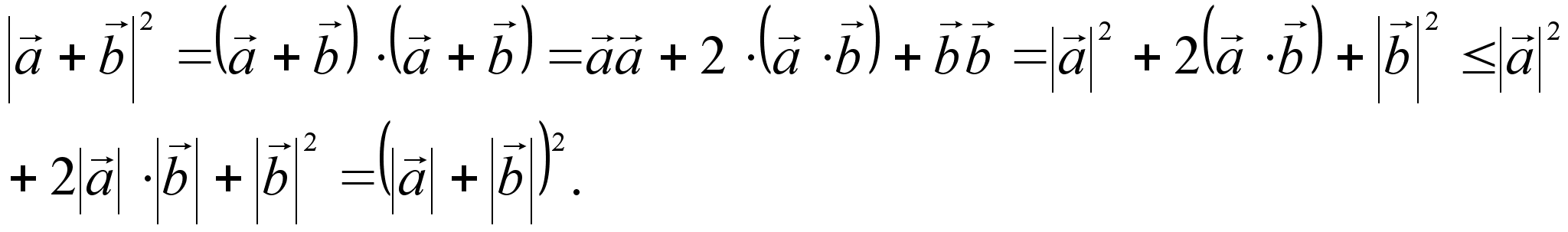
Откуда:

Определение 5.3. Векторы и называются ортогональными, если их скалярное произведение равно 0.

Обозначение: - и - ортогональные векторы.

Итак,