Существуют два ненулевых ортогональных вектора

6. Существуют два ненулевых ортогональных вектора.

Доказательство:

Пусть даны два линейно независимых вектора и .

Рассмотрим два вектора: и .

Подберем l так, чтобы последнее равенство последовательно преобразуем так: =0 Ю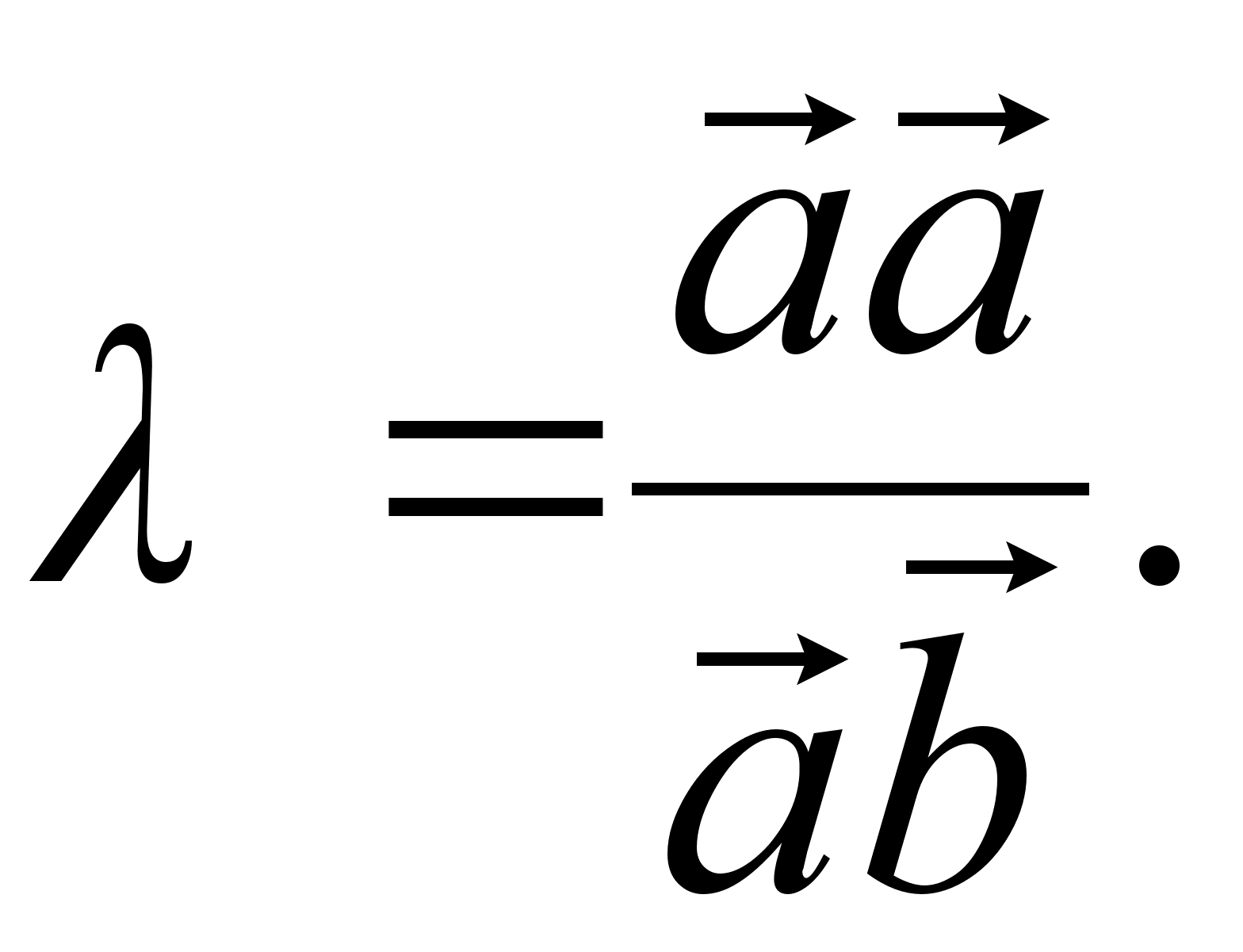

Таким образом, векторы и 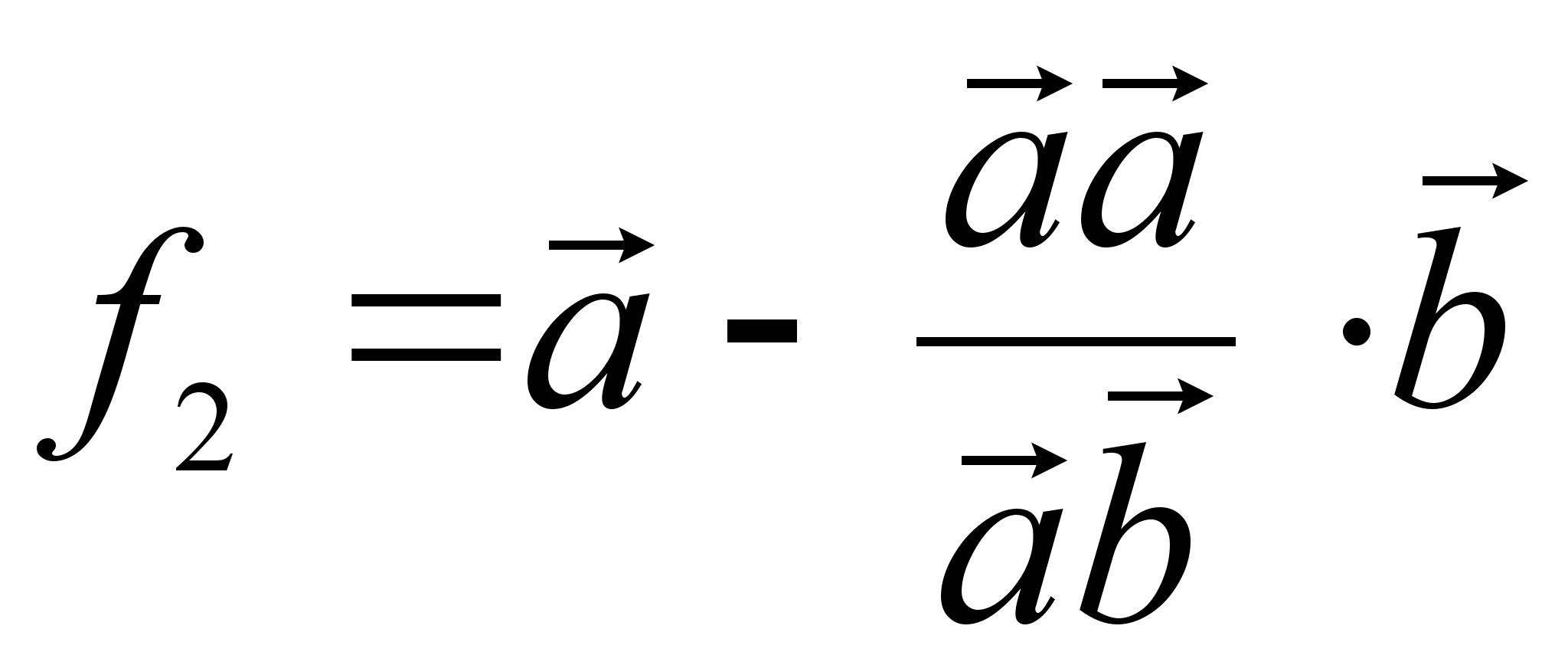ортогональны.

В самом деле:

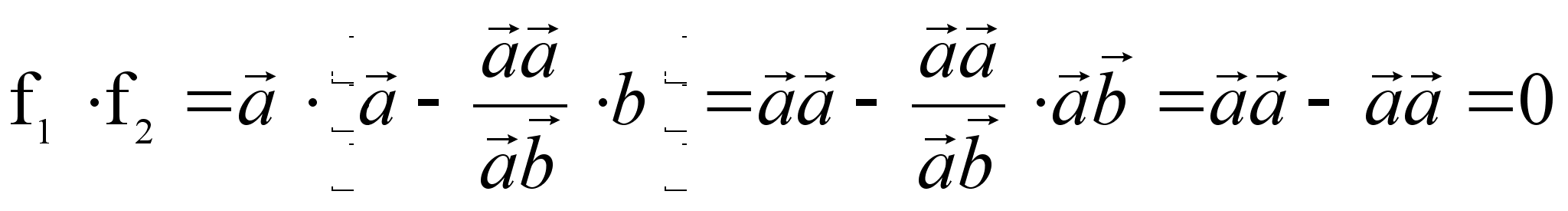
Кроме того, векторы f₁ и f₂ ненулевые.

7.(Теорема Пифагора). Если векторы и ортогональны, то

Доказательство:

Так как Тогда

Определение 5.4. База евклидова пространства называется ортогональной, если для всех

Если при этом еще при , то база называется ортонормированной.

8. Попарно ортогональные ненулевые векторы линейно независимы.

Доказательство:

Пусть векторы попарно ортогональны и все отличны от нулевого вектора. Рассмотрим равенство . Умножая обе части этого равенства последовательно на векторы , получим:

…………………………………………..

Откуда,

Так как , то из полученных равенств следует a₁=a₂=…=a_n=0.

Это означает, что система векторов , линейно независима.

9. Существуют три ненулевых попарно ортогональных вектора.

Доказательство:

Пусть и два ненулевых ортогональных вектора, существование которых обеспечено следствием 6. Подберем ненулевой вектор такой, что и Положим , где - вектор. Образующий с векторами и в условиях следствия 6 линейно независимую систему. Тогда

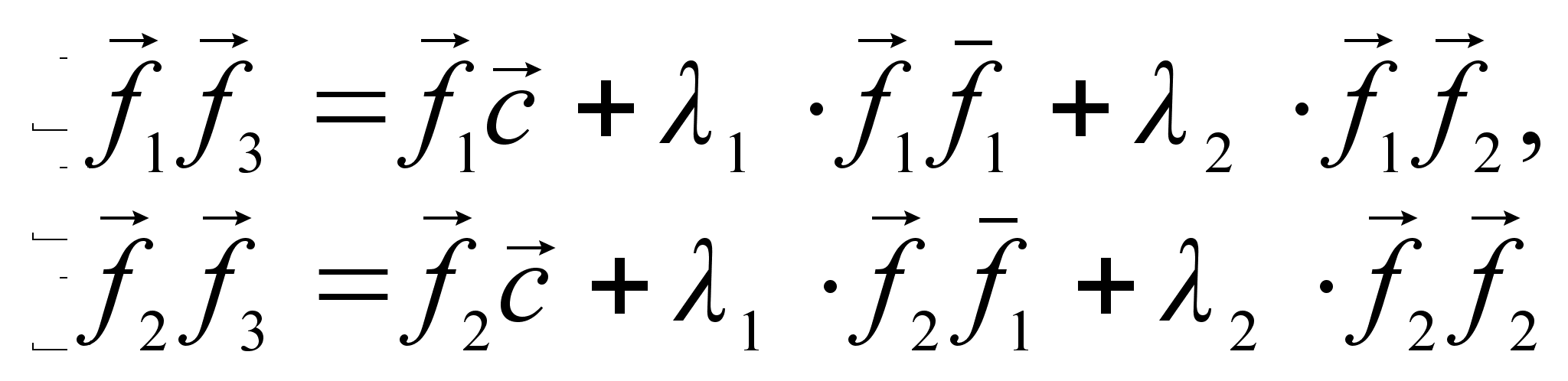
Отсюда

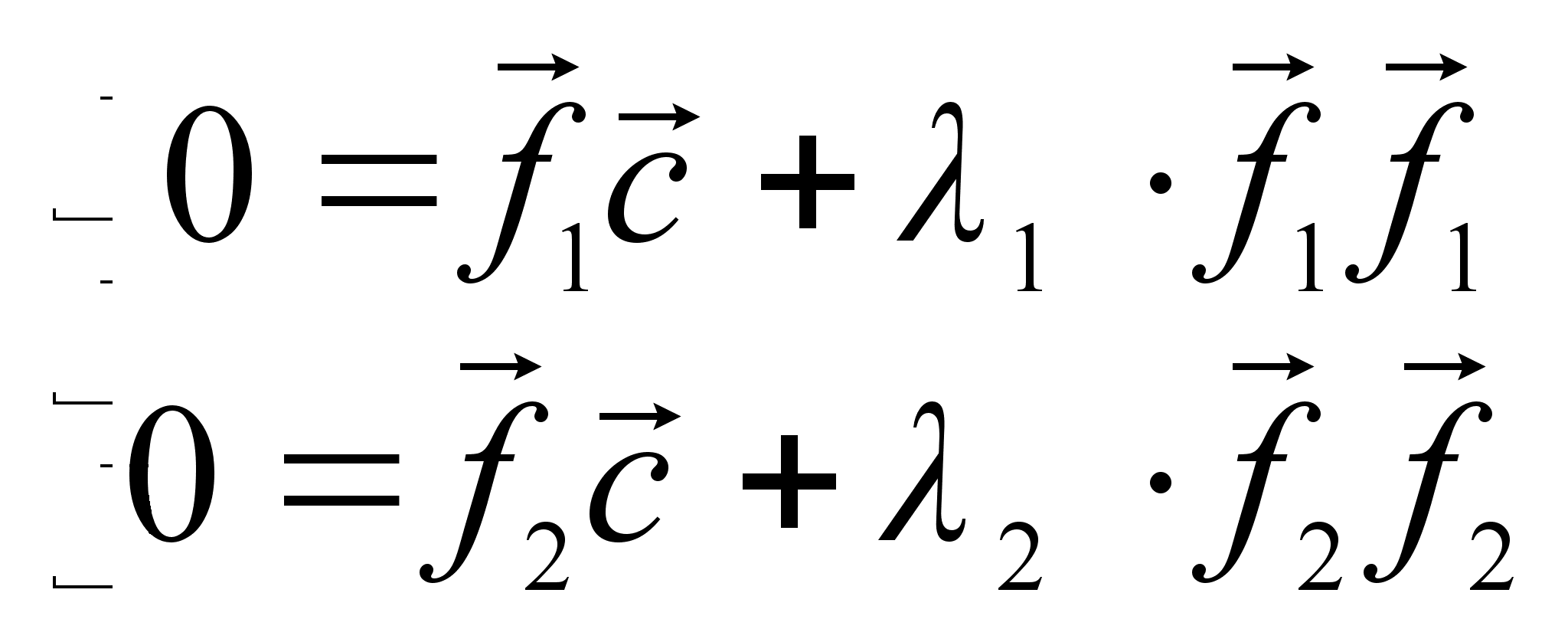
Имеем:

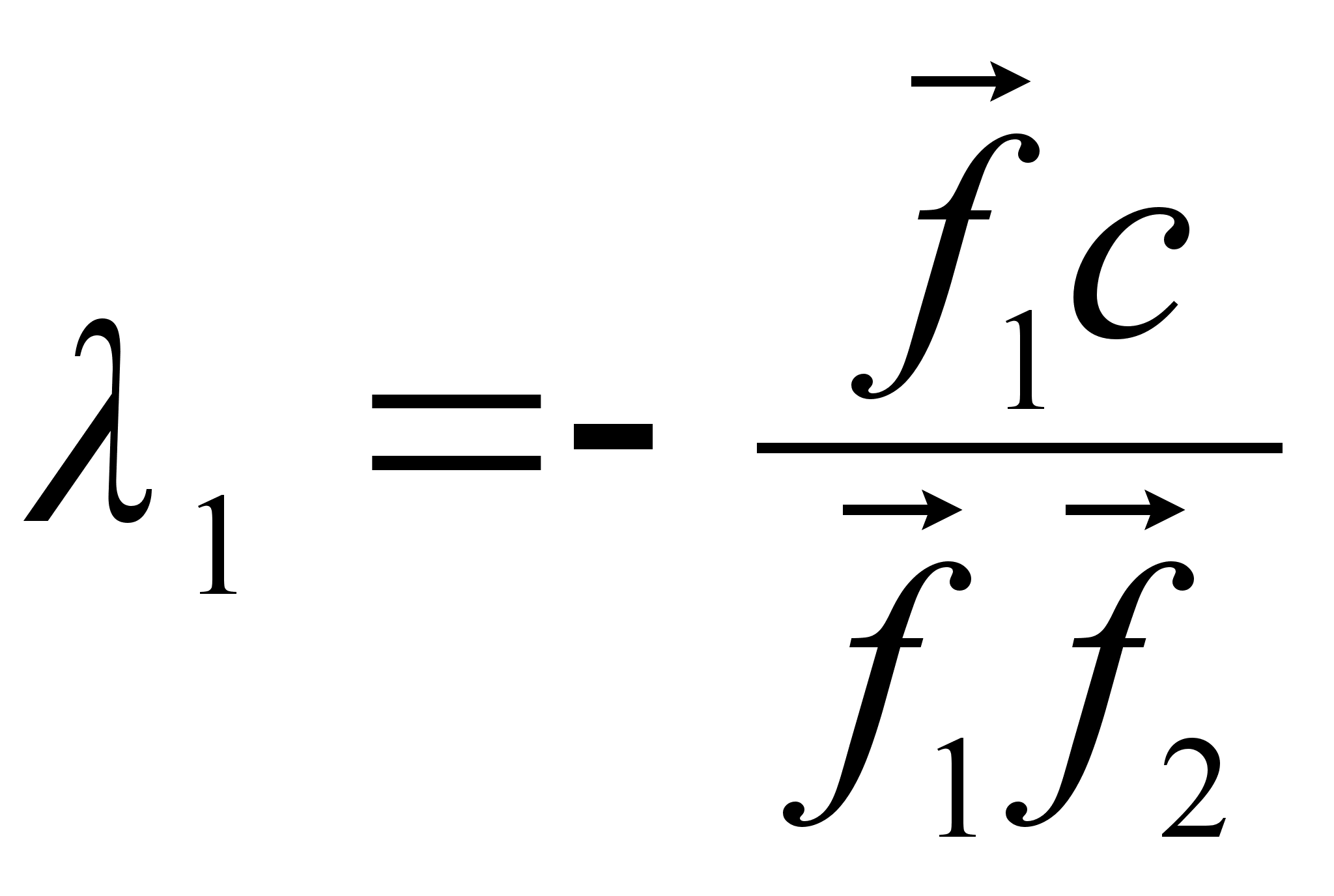и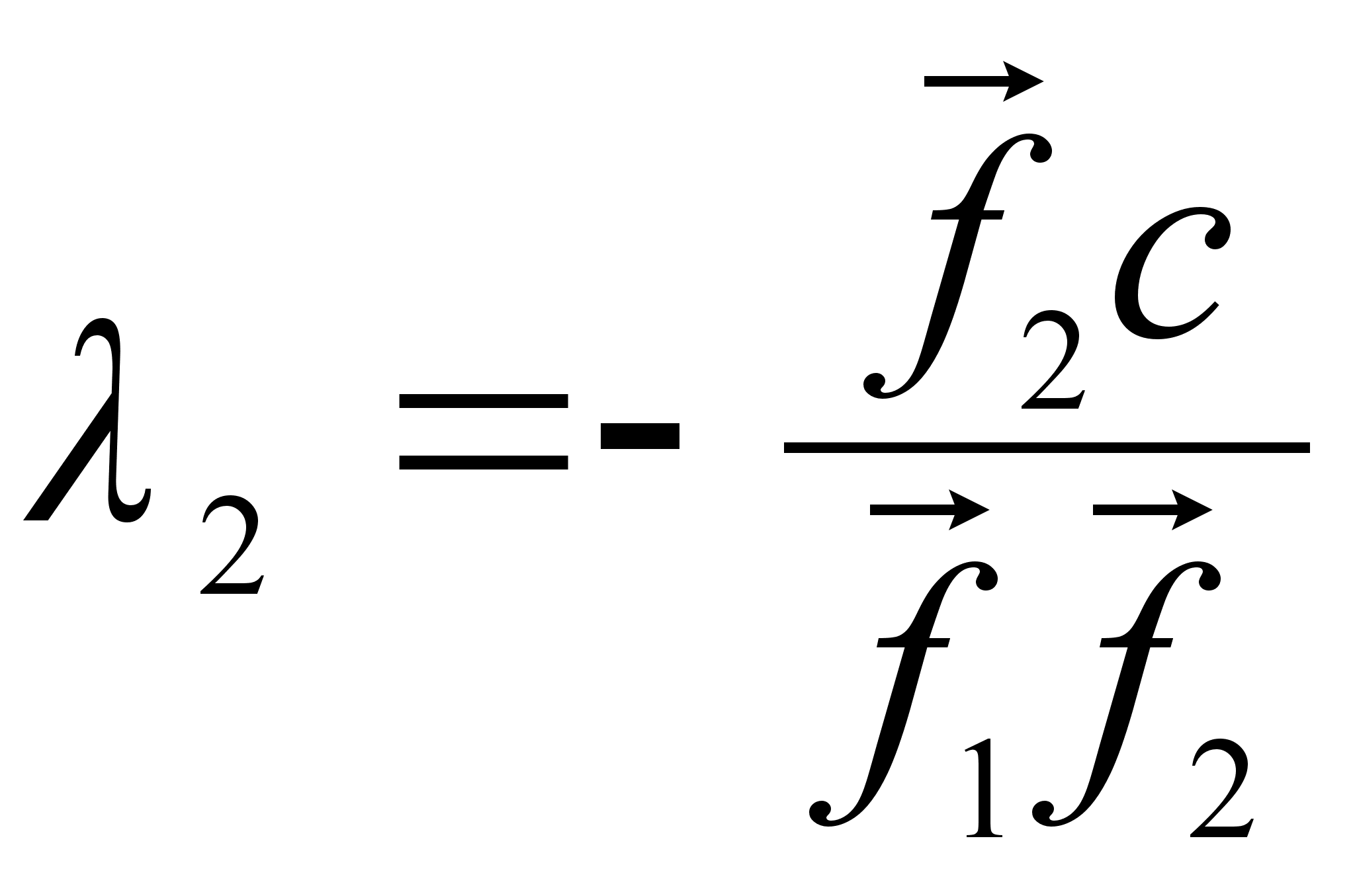

Таким образом, отправляясь от трех линейно независимых векторов и , мы построили три ненулевых вектора , которые попарно ортогональны.

Обобщение. Привлекая последовательно все базы n-мерного евклидового пространства, можно построить аналогично следующие системы ненулевых попарно ортогональных векторов:

…………..

Так как система векторов линейно независима и содержит n векторов (максимальное число линейно независимых векторов), то в результате получена в n-мерном пространстве ортогональная база .

Описанный процесс известен в математике под названием процесса ортогонализации.

Имея ортогональную базу, нетрудно получить с ее помощью ортонормированную базу. Для этого вместо каждого вектора нужно взять вектор

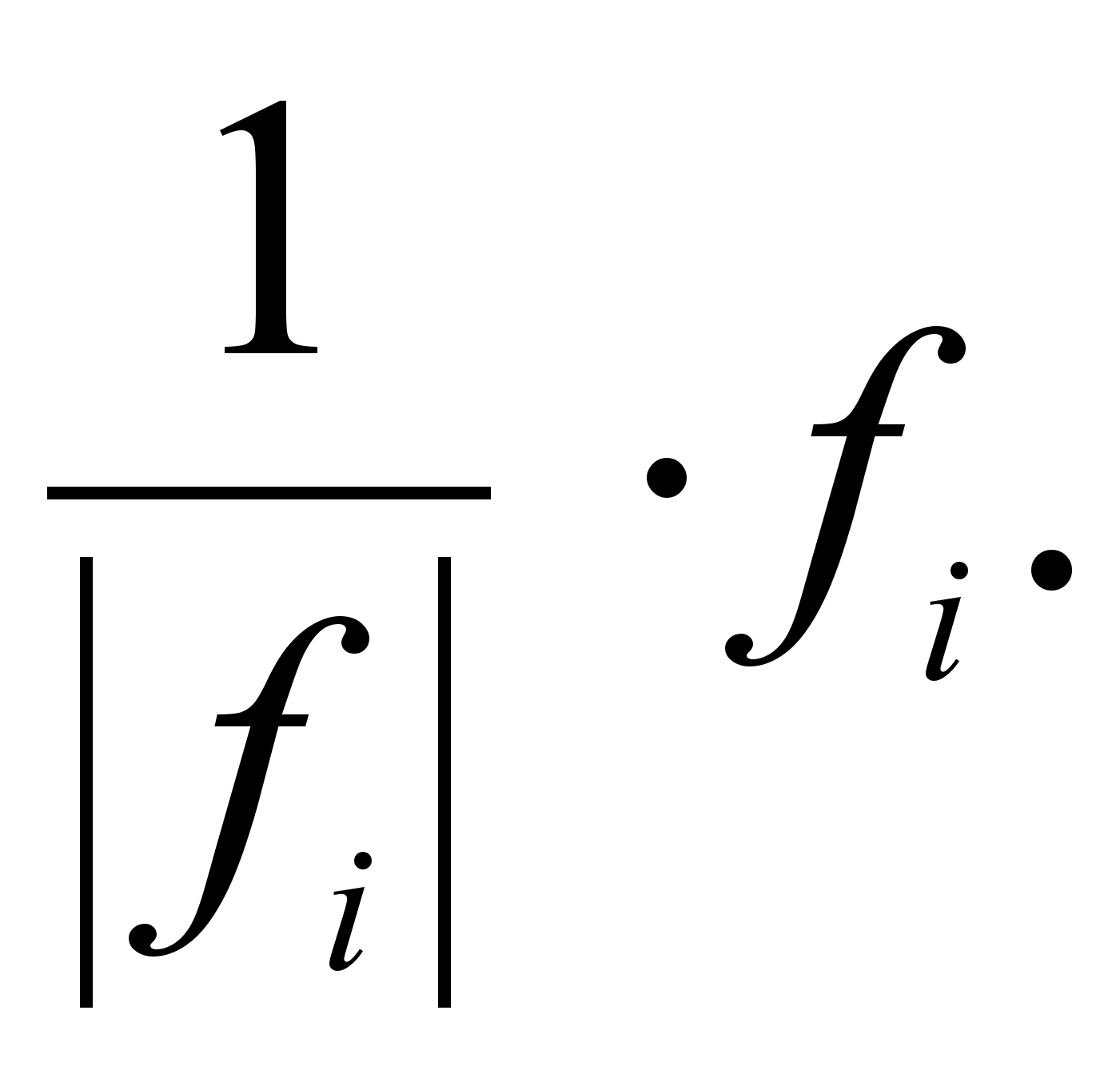
Убедимся, что длина этого вектора равна 1. В самом деле,

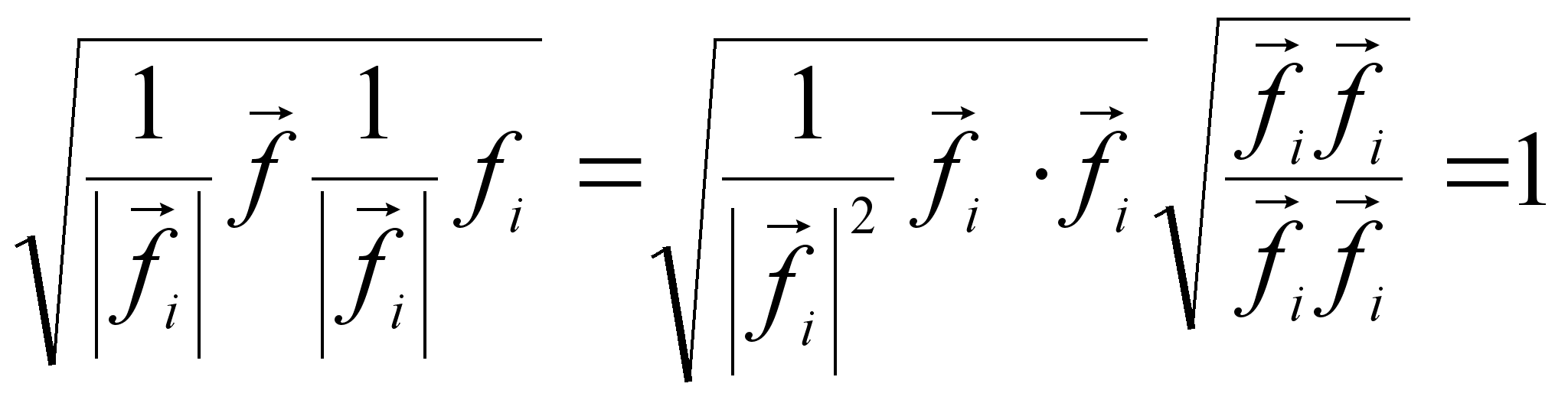
§6. Аксиоматика точечно-векторного евклидова пространства

§6.1. Метрические соотношения в треугольнике

Теорема 18.5. (теорема косинусов для треугольника). Во всяком треугольнике , ,

.

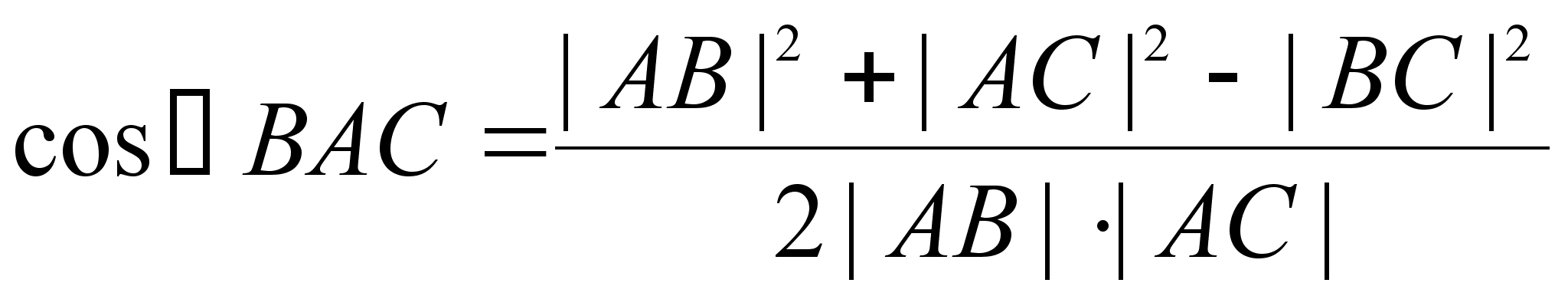
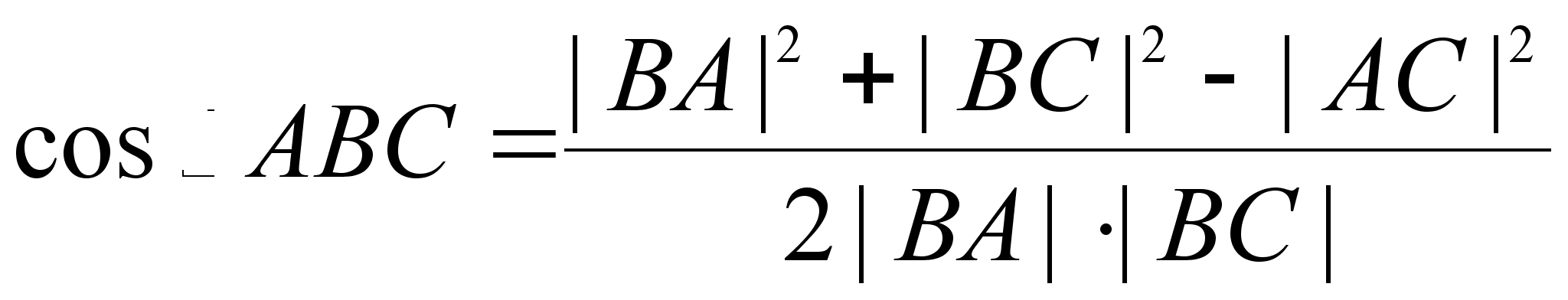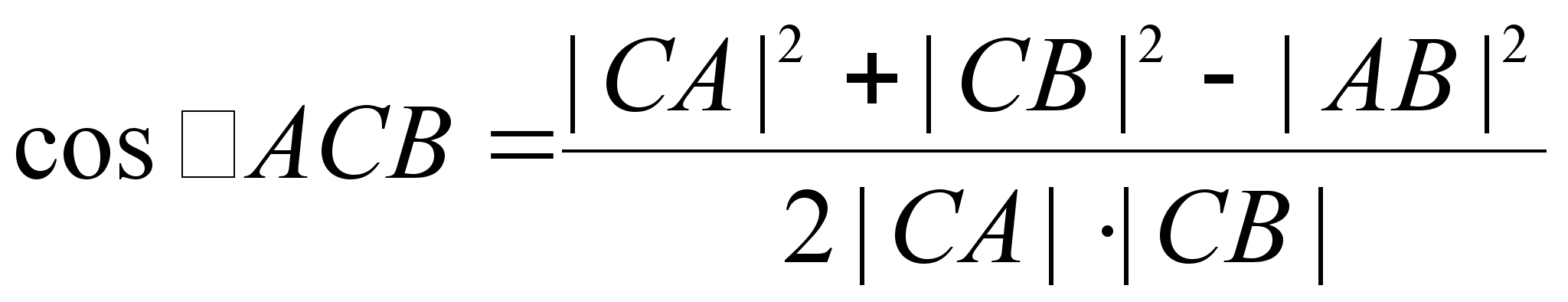Доказательство:

Рассмотрим векторное равенство . Возьмем скалярный квадрат:

,

,

.

Пусть - единичный вектор, отложенный от точка А на луче [АВ), - единичный вектор, отложенный от точки А на луче [АС). Тогда

.

Отсюда

,

.

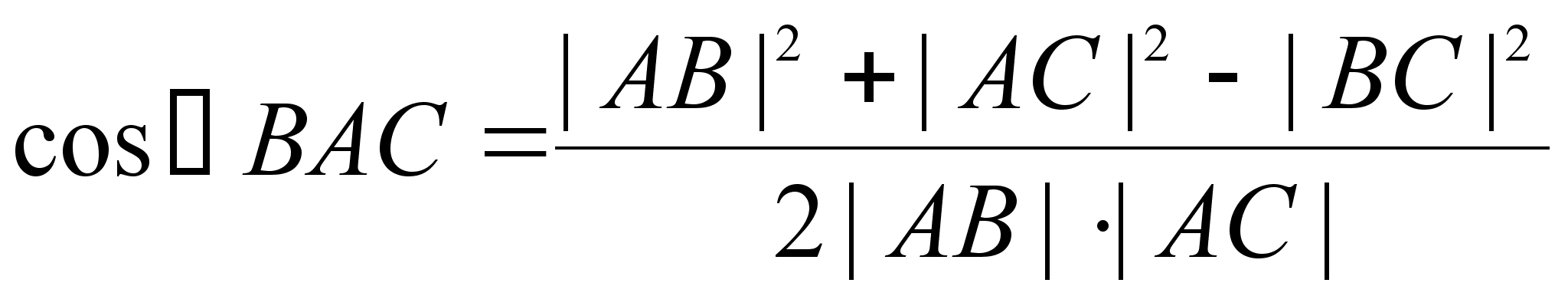Аналогично устанавливаются остальные две формулы теоремы косинусов для треугольника.

Следствие. В треугольнике две стороны конгруэнтны тогда и только тогда, когда лежащие против них углы конгруэнтны.

Доказательство:

I. Пусть . Докажем, что .

Имеем

.

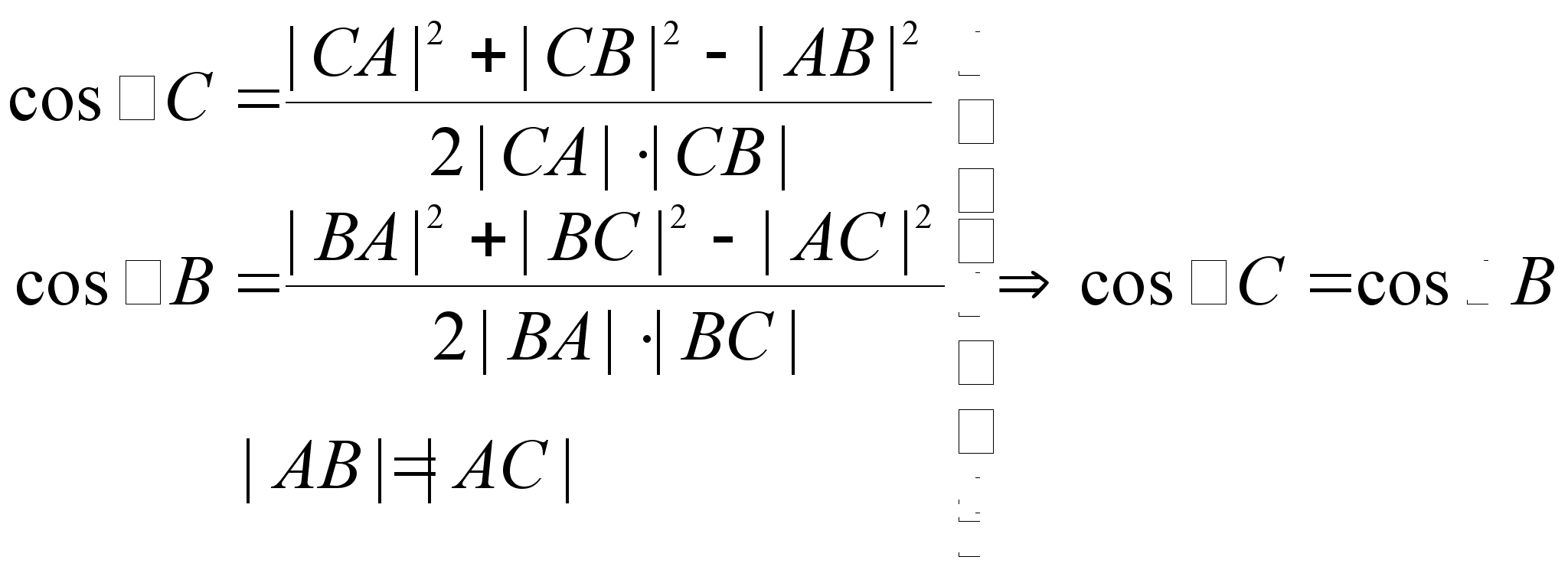II. Пусть . Докажем, что . Выполним следующие преобразования

– ,

,

,

,

.

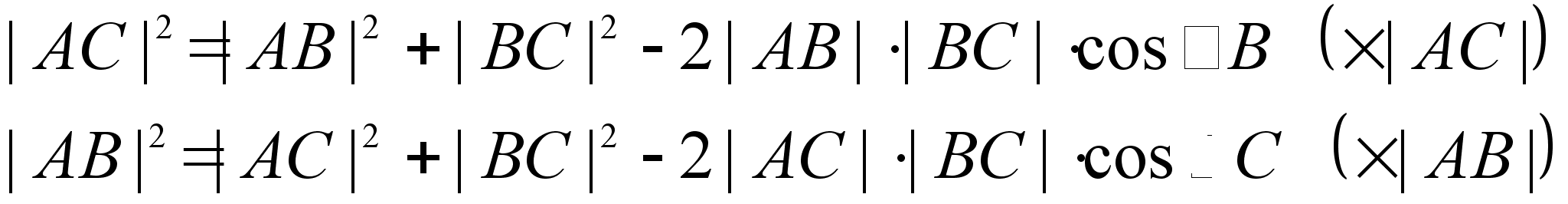Докажем, что ; то ;

, но для треугольника .

Таким образом,

.

Теорема 18.6.

, (1)

(2)

(3)

Доказательство:

Докажем равенство (1). Рассмотрим равенство: . Умножим его скалярно на :

, или так как , то

, или

, это и есть равенство (1).

Аналогично устанавливается остальные соотношения.

Следствие 2. Если один из углов в треугольнике тупой, то два других острые.

Доказательство:

Пусть – прямой, то есть .

Имеем:

,

.

Тогда:

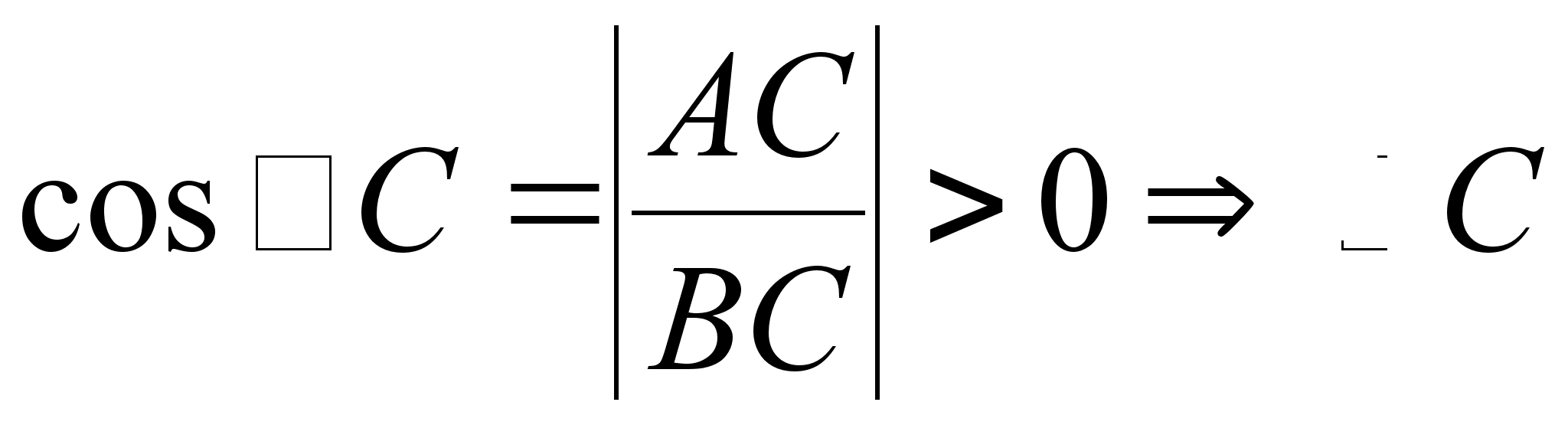– острый,

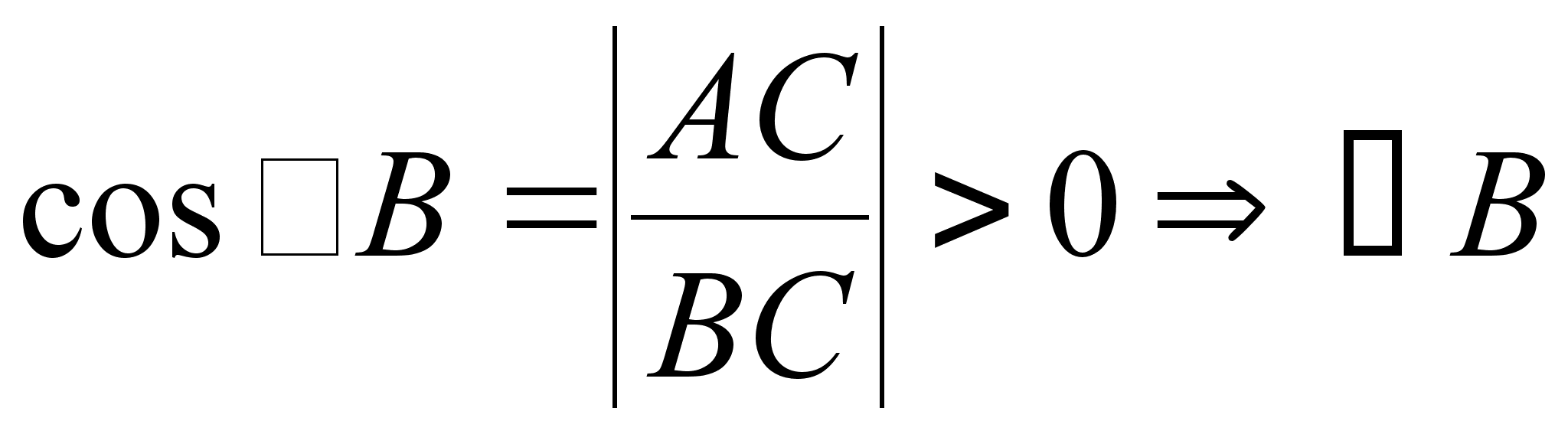– острый.

Следствие 3. В треугольнике более одного тупого угла быть не может.

Доказательство:

Пусть – тупой угол, то есть .

Тогда 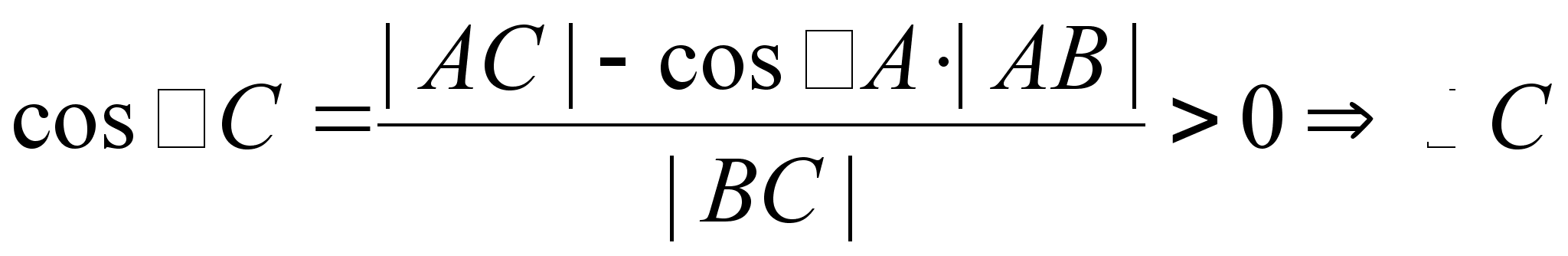– острый.

Аналогично устанавливается, что – острый.

Определение 18.6. Треугольник называется прямоугольным, если он имеет прямой угол.

Теорема 18.7. (теорема Пифагора). Если в – прямой, то .

Доказательство:

Имеем: .

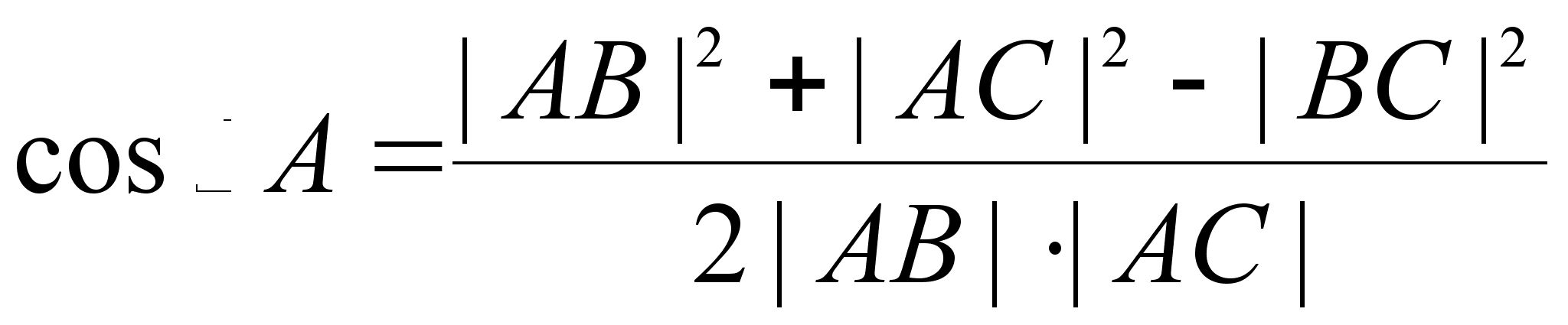Так как – прямой, то .

Тогда .

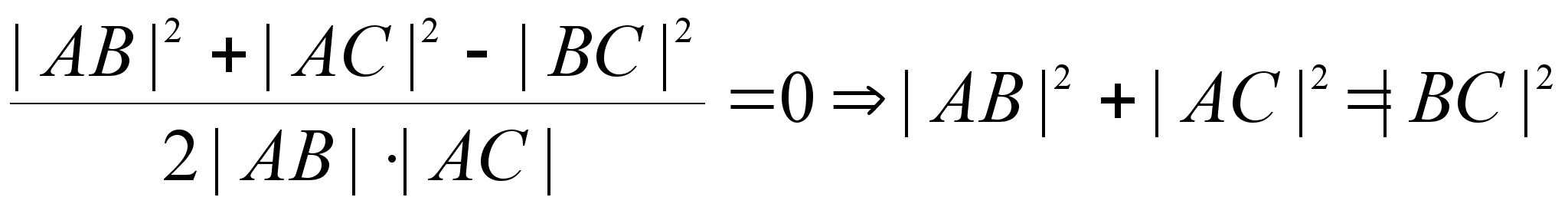Теорема 18.8. (обратная теорема 18.7). Если в , то этот треугольник прямоугольный.

Доказательство получается в результате проведения предыдущих рассуждений в обратном порядке.

Следствие 4. В прямоугольном треугольнике каждый катет меньше гипотенузы.

Доказательство:

Пусть , тогда имеем:

,

.

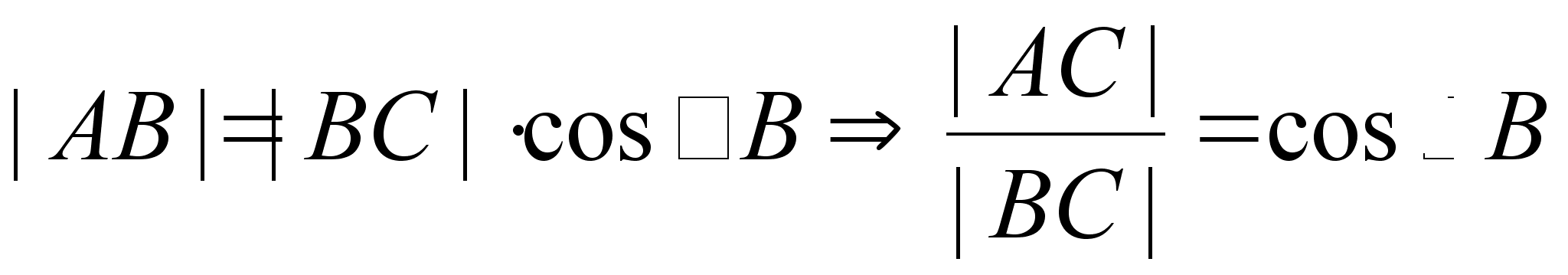Так как углы С и В острые, то и .

Отсюда 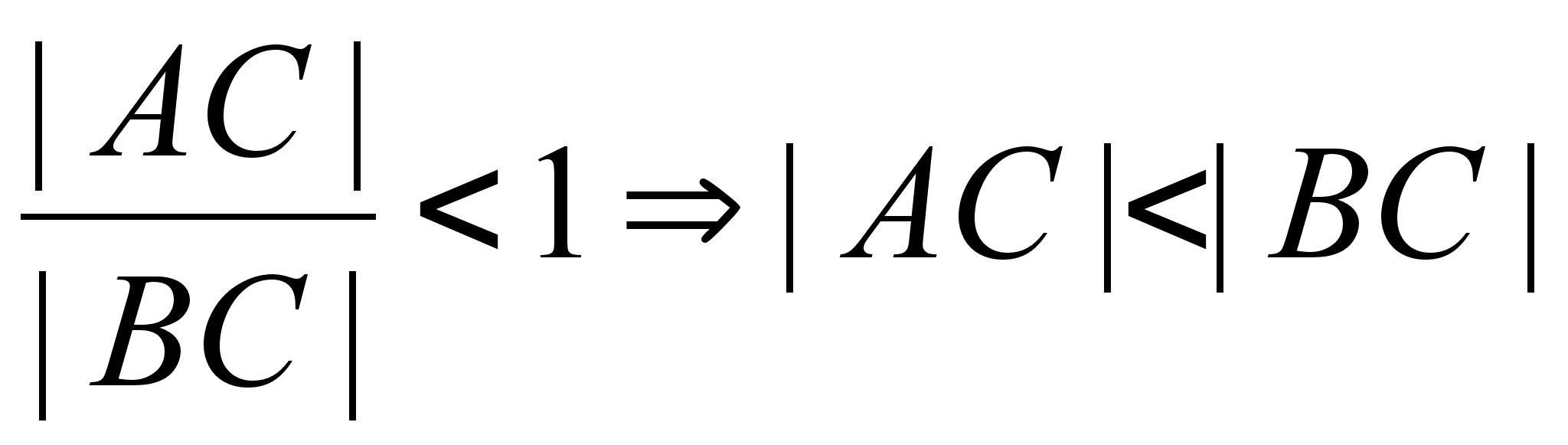и .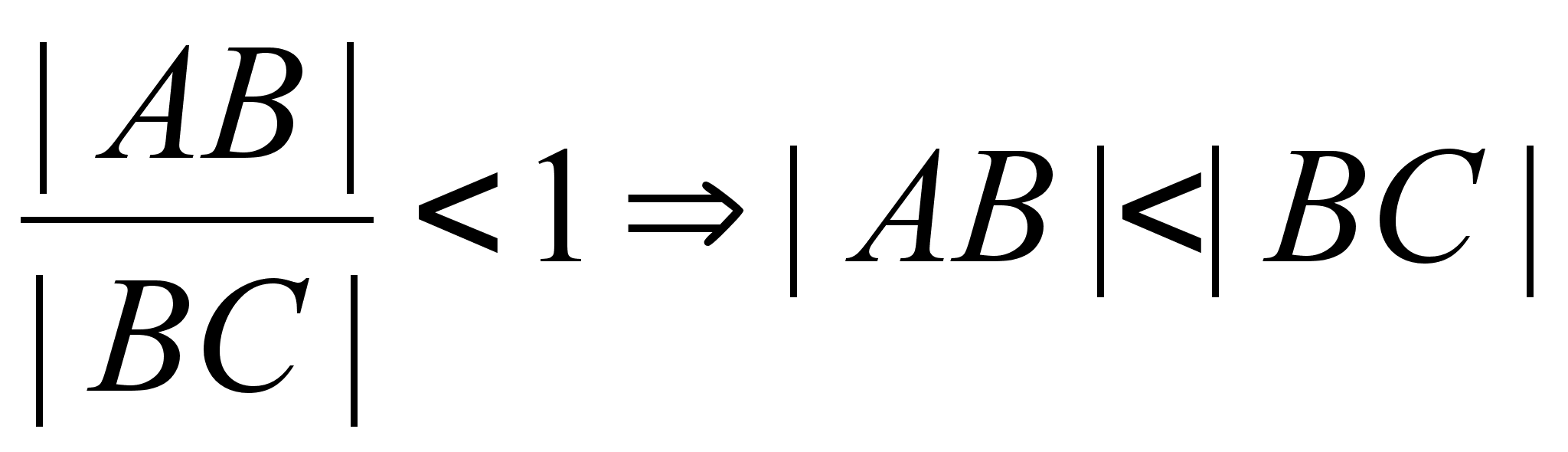

§6.2. Конгруэнтность треугольников

Определение 18.7. Если треугольник АВС называется конгруэнтным треугольнику А₁В₁С₁, если ,

.

Обозначение: 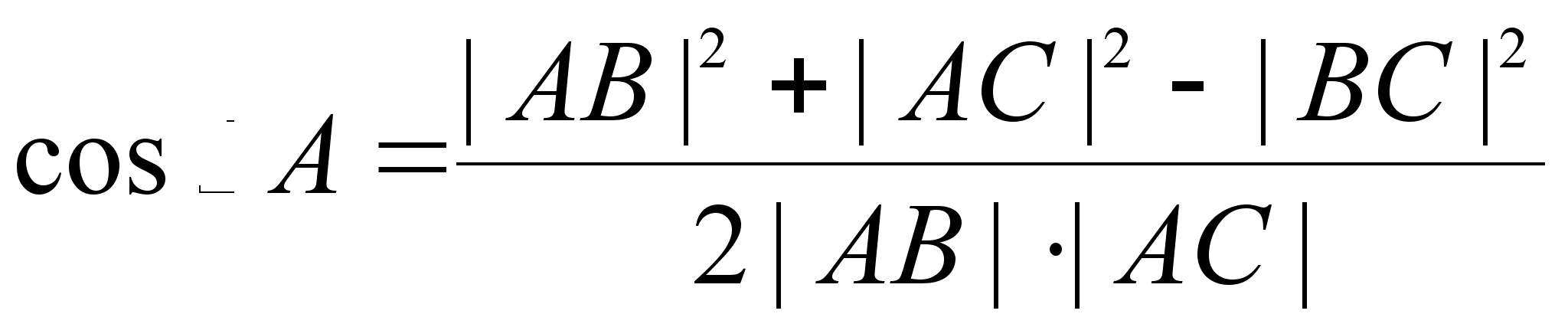– треугольник АВС называется конгруэнтным треугольнику А₁В₁С₁. Теорема 18.9. Если , то . Доказательство: Имеем: , (1)

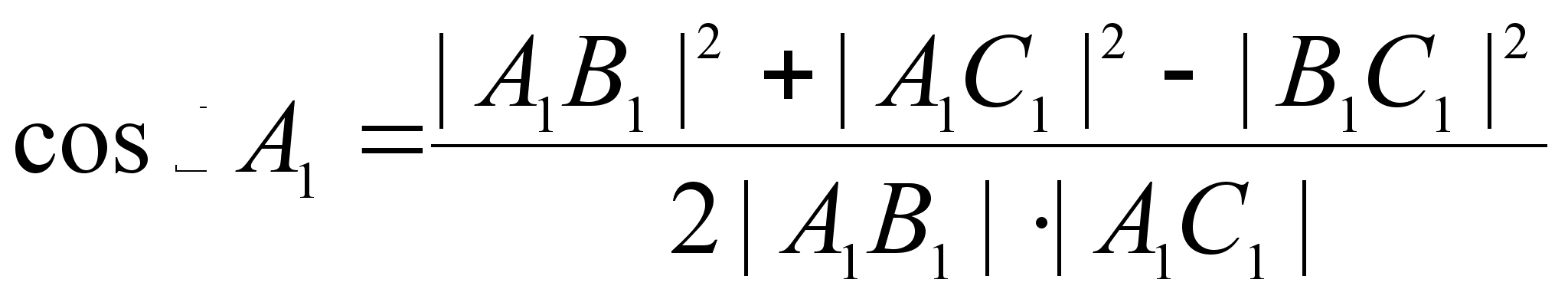(2)

По условию теоремы .

Отсюда и из равенств (1) и (2) следует, что , то есть

Аналогично устанавливается и соотношения , . Отсюда .

Теорема 18.10. Если и

то .

Доказательство:

На основании теоремы 18.5. имеем:

,

.

Отсюда, учитывая условия теоремы, получим , то есть .

На основании предыдущей теоремы .

Теорема 18.11. Если , и , .

Доказательство:

Если , то доказанному выше . Если , то отложим на луче [АС) от точки А отрезок [А₁С₁] (рис.):

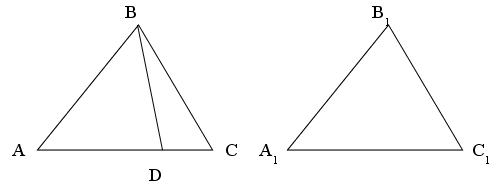
. Тогда на основании предыдущей теоремы . Из конгруэнтности этих треугольников следует, что . Имеем: на луче [ВА) в полуплоскости, содержащей точку С, отложены два угла (различных) и , конгруэнтных одному и тому же углу . Последнее противоречит теореме 18.4., следовательно и .

§7. Элементы тригонометрии

§7.1. Билинейная кососимметричная функция

Определение 19.1. Если каждым двум векторам и ставится в соответствие каждое действительное число такое, что:

1) ;

2) ;

3) .

то функция называется билинейной кососимметрической функцией.

Теорема 19.1. Пусть и – произвольная база плоскости и – некоторое действительное число. Тогда существует одна и только одна кососимметрическая функция такая, что:

.

Доказательство:

Пусть в заданном базисе два произвольных вектора и имеют разложения:

Составим функцию

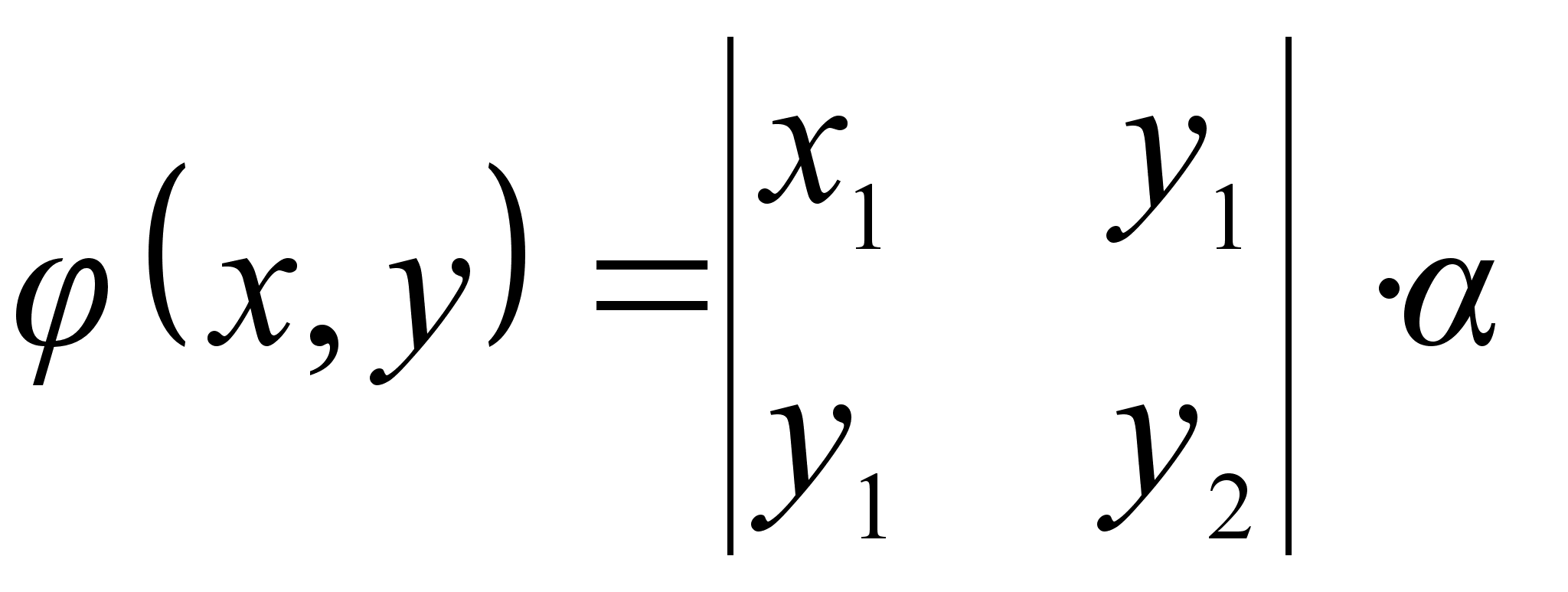(1)

Нетрудно проверить, что билинейная кососимметрическая функция, причем, если , то

.

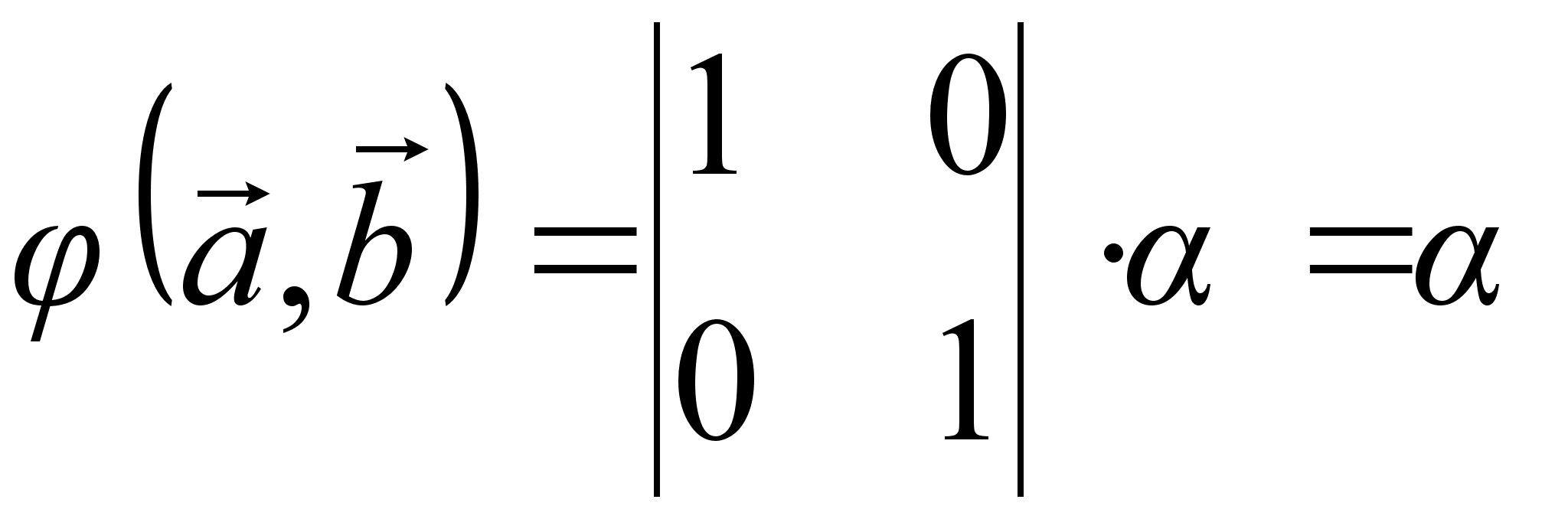Доказательства единственности. (методом от противного).

Допустим, что существует билинейная кососимметрическая функция

, такая, что .

Если – билинейная функция, то

= =

= =

= .

Учитывая, что , получим .

Аналогично . Кроме того, . Тогда

По предположению . Поэтому:

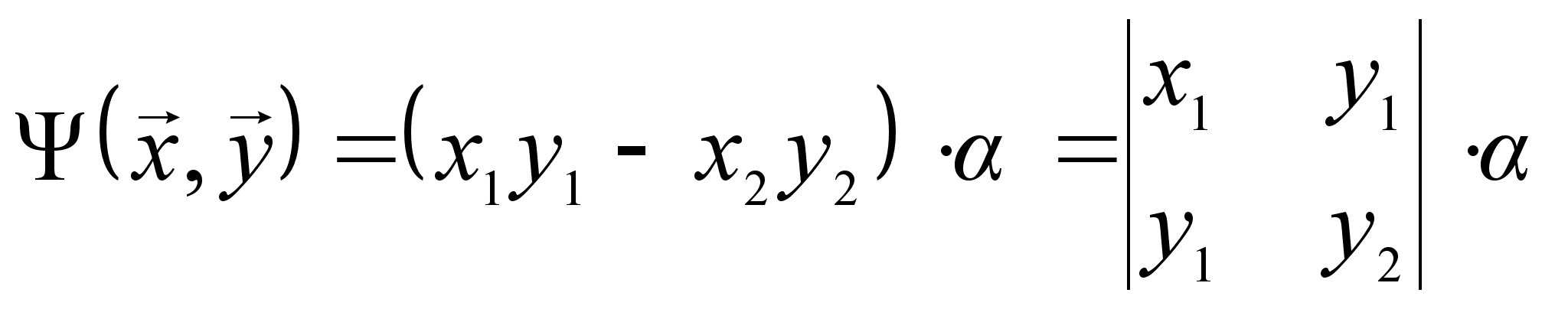(2)

Из (1) и (2) следует, что .

Примечание. Из проведенного рассуждения видно, что какое бы число мы ни взяли и какую бы мы ни взяли базу векторов и , существует единственная билинейная кососимметрическая функция такая, что .

Это обстоятельство говорит, что с помощью кососимметрической функции нельзя отличить ортонормированную базу от прочих. На этот счет требуется специальное соглашение. Договоримся, если база ортонормированная, то будем полагать .

Определение 19.2. Пусть – два произвольных единичных вектора. Значение билинейной кососимметрической функции при выбранном ортонормированном базисе , и выполнении соглашения называется синусом угла между векторами и .

Итак,

В иной форме:

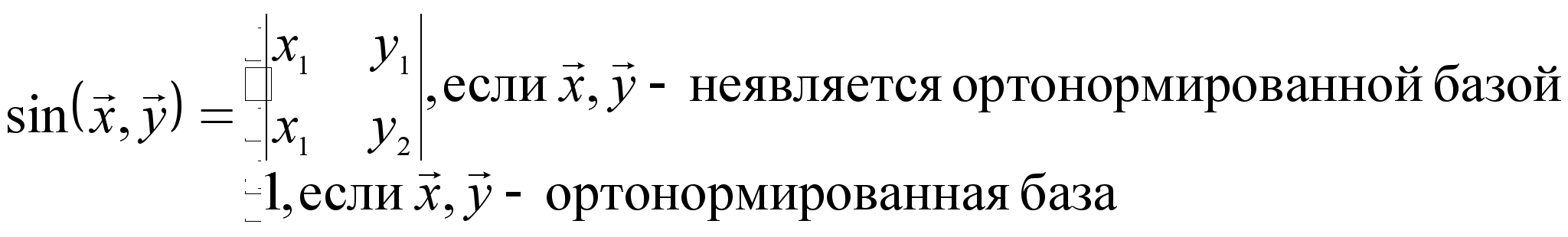
Теорема 19.2. или . На основании определения 19.2. имеем:

.

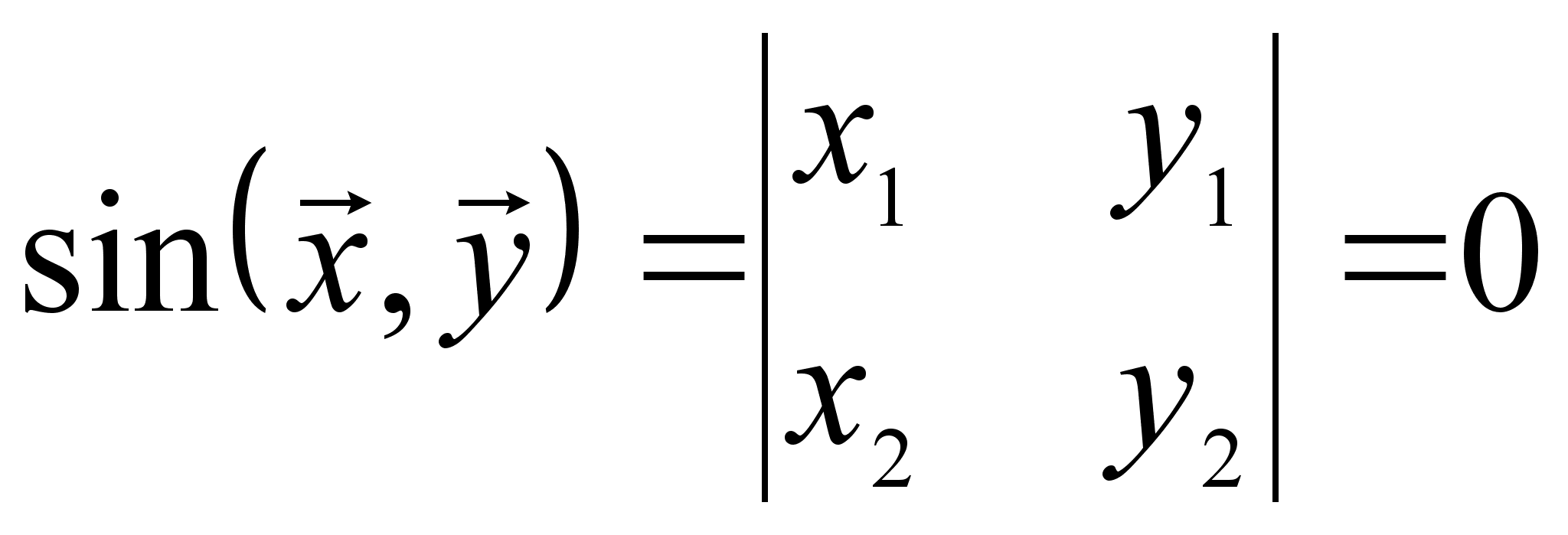Отсюда,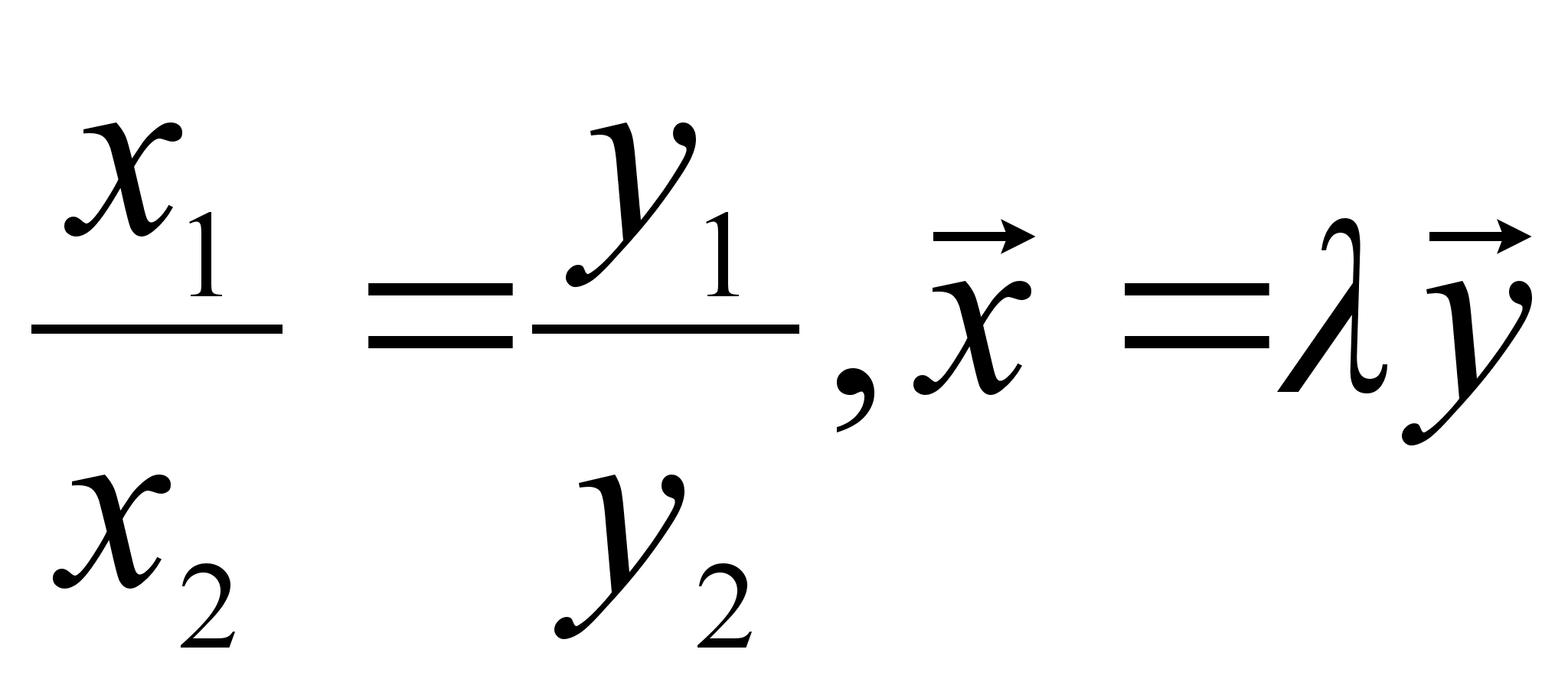. Докажем достаточность. Пусть , где .

Докажем, что .

В силу определения 19.2. имеем:

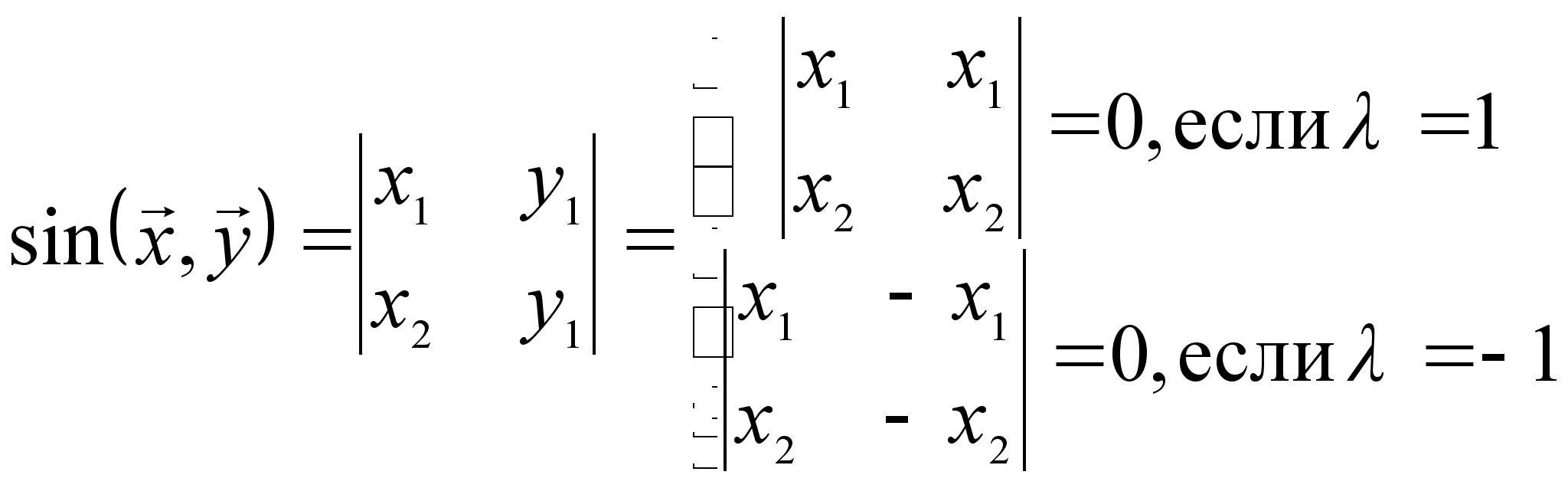
Теорема 19.3. .

Доказательство: Пусть – единичные векторы и . Имеем:

,

Тогда

.

§7.2. Геометрическое истолкование косинуса и синуса угла между двумя единичными векторами

В

Н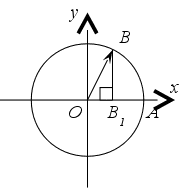а основании соотношения

Для произвольного треугольника имеем (рис.).

Так как , то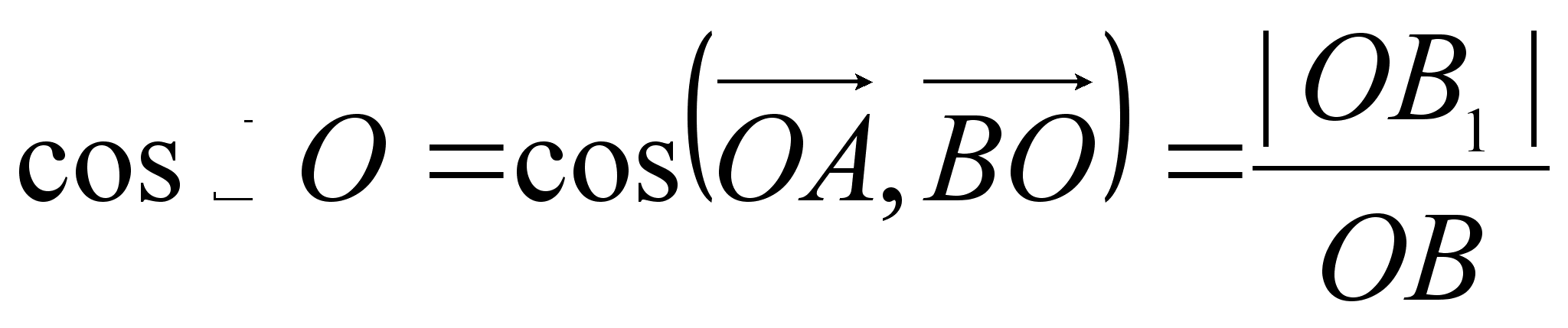

Наша окружность единичного радиуса ,

поэтому:

Таким образом, косинус угла между двумя единичными векторами и есть длина отрезка, который является проекцией отрезка [ОВ] на прямую (ОА), причем эта длина берется со знаком «+» если и со знаком «–» если .

Из соотношения имеем, что геометрически представляет собой длину катета или проекцию единичного вектора ОВ на ось у, причем в верхней полуплоскости .

§7.3. Основные соотношения между тригонометрическими функциями

Пусть и два единичных вектора. Непосредственно из определений следует, что ,

, , если

, если

Теорема 19.4.

Доказательство:

Пусть – единичные векторы, .

Положим,

,

,

На основании определений 18.5 и 19.2. имеем:

.

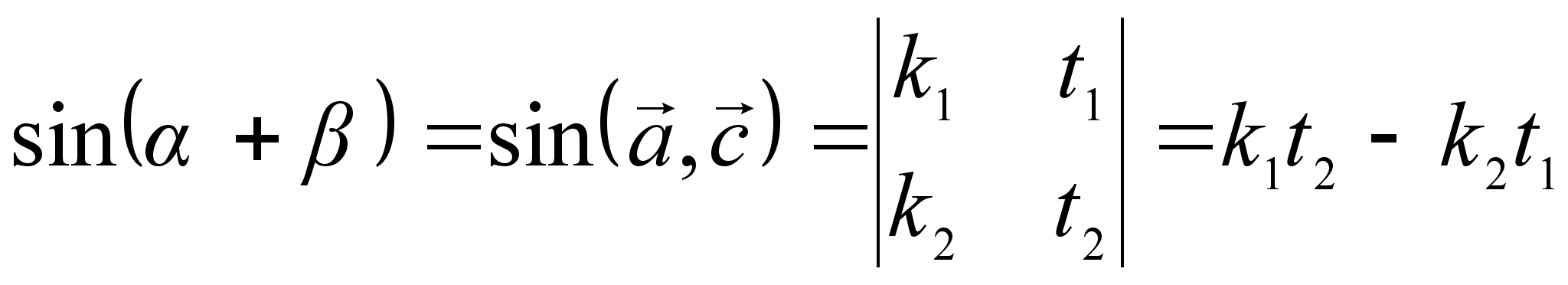Выполнив несложные преобразования, получим:

, или ,

, или ,

или ,

или .

Тогда

Следствие 19.1.

Доказательство: