Навигация
Билеты по геометрии (11 класс)
Билет № 3
1. Взаимное расположение прямой и плоскости в пространстве
2. Объем призмы.
1.Три случая расположения прямой и плоскости.
1.Плоскость и прямая имеют одну оющую точку a ÈA
2.Прямая лежит в плоскости а значит имеет с ней 2 общие точки.
1.Пряммая и плоскость не имеют общих точек т.е.a÷ï a
2.Теорема: Объем прямой призмы равен произведению площади основания на высоту.
Д-во: Рассмотрим правильную 3-угольную призму АВСА1В1С1с объемом V и высотой h.
Проведем такую высоту ∆АВС (ВD) кот. разделит этот ∆на 2 ∆. Поскольку ВВ1D разделяют данную призму на 2 призмы , основания кот является прямоугольный ∆ABD и ВСD. Плэтому объем V1 и V2 соответственно равны SABD ·h и SВСD ·h. По св-ву 20 объемов V=V1+V2 т.е V= SABD ·h+ SВСD ·h= (SABD+ SВСD) h. Т.о. V=SАВС·h
Д-во Возьмем произвольную прямую призму с высотой h и площадью основания S. Такую
призму можно разбить на прямые треугольные призмы с высотой h. Выразим объем каждой треугольной призмы по формуле (1) и сложим эти объемы. Вынося за скобки общий множитель h, получим в скобках сумму площадей оснований треугольных призм, т. е. площадь S основания исходной призмы. Таким образом, объем исходной призмы равен произведению Sh. Теорема доказана.
Рассмотрим случай , когда призмая является частью параллелепип-ида. Диогональное сечение делит параллелепипед на 2 равные треугольные призмы. Так как Sпол = 1//2 ab то S∆=ab =>V∆= Sh ч.т.д.
Билет №5
1. Перпендикуляр к наклонной плоскости(формулировки, примеры)
2. Объем цилиндра.
1.Рассмотрим пл α и т А, не лежащую в этой плоскости. Проведем через т А прямую,^ к пл α, и обозначим букв H т пересечения этой прямой с пл α .Отрезок АН называется, ^ проведенным из
т А к пл α, a т Н — основанием ^. Отметим в пл α какую-нибудь т М,отличную от Н, и проведем отр AM.Он называется наклонной, про-вед из т А к пл α , а т М — основанием наклонной. Отрезок НМ наз-ывается проекцией наклонной на пл α. Сравним ^ АН и наклон-ную AM: в прямоугольном ∆АМН сторона АН — катет, а сторона AM - гипотенуза, поэтому АН<АМ. Итак, ^, проведенный аз данной т к пл, меньше любой наклонной, проведенной из той же т к этой пл.
=> из всех расстояний от т А до различных т пл α наименьшим является расстояние до т H. Это расстояние, т. е: длина ^, проведенного из т А к пл α , называется расстоянием от т A до пл α
Замечаиия. 1. Если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости.
2. Теорема. Объем цилиндра равен произведению площади основания на высоту.
Д-во. Впишем в данный цилиндр Р радиуса r и высоты h правильную n-угольную призму Fn а в
эту призму впишем цилиндр Рп . Обозначим через V и Vn объемы цилиндров Р и Рп, через rп — радиус цилиндра Рп. Так как объем призмы Fn равен Snh, где Sn- площадь основания призмы, а цилиндр Р содержит призму Fn , кот в свою очередь , содержит цилиндр Рп , тоVn<Snh<V. Будем неограниченно увеличивать число n. При этом радиус rп цилиндра Рп стремиться к радиусу r цилиндра Р(rп=rcos180/n®r при r→∞). Поэтому V цилиндра Рп стремиться к объему цилиндра Р: limVn=V. Из равенства (Vn<Snh<V) =>, что
n→∞
limSnh=V. Но limSn=πr2 Т.о V=πr2h. т.к πr2=S , то получим V=Sоснh.
n→∞ n→∞
Билет № 61. Расстояние между скрещивающимися прямыми (формулировки, примеры)
2. Объем конуса.
Расстояние между одной из скрещивающихся прямых и плоскостью , проходящей через другую прямую параллельную первой , называется расстояни6е между скрещивающимися прямыми.
Если две прямые скрещиваются то через каждую из них проходит плоскость параллельная другой прямой , и при том только одна.
2 Теорема. Объем конуса равен одной трети произведения площади основания на высоту.
Д-во Рассмотрим конус с объемом V, радиусом основания R, высо-той h и вершиной т О . Введем ось Ох (ОМ). Произвольное сечение конуса пл. , ^ к оси Ох , является кругом с центром в т М1 пересе-чения этой пл. с осью Ох. Обозначим радиус через R1 ,а S сечения через S(х) , где х – абсцисса т М1 . Из подобия прямоугольных ∆ ОМ1А1 и ОМА=> что
| ОМ1 | = | R1 | , или | x | = | R1 | откуда | R= | xR | так как | S(x)= pR12 | ,то | S(x)= | pR2 |
| ОМ | R | h | R | h | h2 |
Применяя основную формулу для вычисления объемов тел при а=0, b=0, получим
|
| h |
|
|
| h |
|
|
| h | |||
| V= | ∫ | πR2 | x2dx= | πR2 | ∫ | x2dx= | πR2 | × | x3 | ½= | 1 | πR2 h |
| h2 | h2 | h2 | 3 | 3 | ||||||||
|
| 0 |
|
|
| 0 |
|
|
| 0 | |||
Площадь S основания конуса равна pR2, поэтому V=1/3Sh.
Следствие. Объемом V усеченного конуса , высота кот равна h, а площадь оснований S и S1вычисляется по формуле V=1/3h(S·S1+√ S·S1).
Билет №7
Похожие работы
... отрезка пополам с помощью циркуля и линейки. БИЛЕТ 6 1.Средняя линия трапеции. Теорема о средней линии трапеции. 2.Простейшие задачи в координатах. БИЛЕТ 7 1.Параллелограмм. Свойства параллелограмма (доказательство одного из них). 2.Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Вывод одной из них. БИЛЕТ 8 1.Параллелограмм. ...
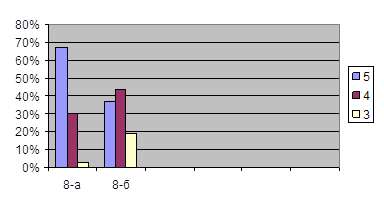
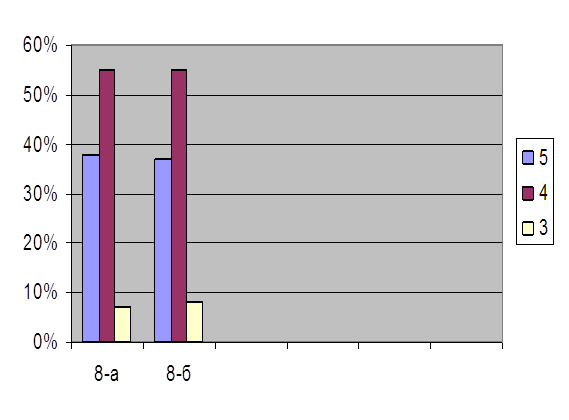
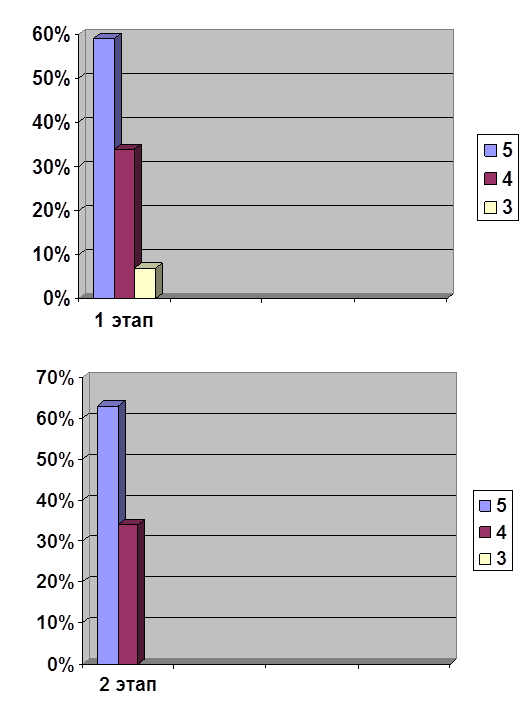
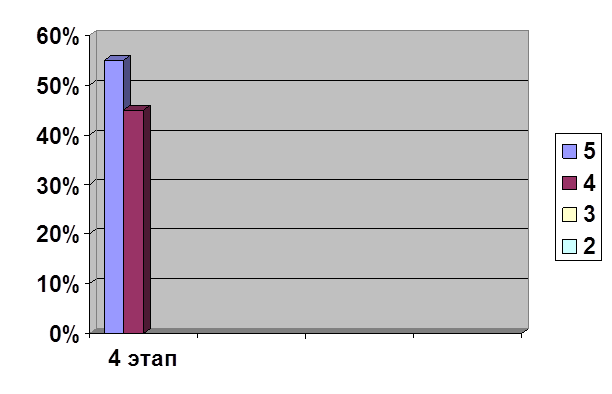
... прежнем уровне. В экспериментальном классе, котором были проведены ряд зачетных уроков, повысился уровень знаний. В ходе написания выпускной квалификационной работы по теме « Зачет как одна из форм контроля знаний учащихся по алгебре в 8 классе» были реализованы поставленные цели и задачи. Гипотеза дала положительный результат. Таким образом, разнообразие форм проверки знаний и их сочетания в ...
... зарождения и восприятия знаний от социокультурного контекста · Изучить роль личности, её индивидуального пути в становлении самой науки. 2. Периодизация истории психологии. См. билет 1 вопрос 1 Билет 3. 1. Возникновение и противостояние идеалистического и материалистического взглядов на природу психического в древности. Появление психологии в Древней Греции на рубеже VII ...
... по звездной карте склонение Солнца на данный день и вычисление его высоты в полдень. H = 900 - + = 560 h – высота светила БИЛЕТ № 8 Важнейшие направления и задачи исследования и освоения космического пространства. Основные проблемы современной астрономии: Нет решения многих частных проблем космогонии: · Как сформировалась Луна, как образовались кольца вокруг планет ...

0 комментариев