Однофакторный дисперсионный анализ
Многофакторный дисперсионный анализ
Применение дисперсионного анализа в различных процессах и исследованиях
Грипп вызывает повышенную выработку гистамина
Купирование острой психотической симптоматики у больных шизофренией атипичным нейролептиком
Снование фасонной пряжи с ровничным эффектом
Дисперсионный анализ в контексте статистических методов
Векторные авторегрессии
Факторный анализ
Парная регрессия. Вероятностная природа регрессионных моделей
Навигация
Многофакторный дисперсионный анализ
Дисперсионный анализ
75320
знаков
5
таблиц
6
изображений
1.3 Многофакторный дисперсионный анализ
Следует сразу же отметить, что принципиальной разницы между многофакторным и однофакторным дисперсионным анализом нет. Многофакторный анализ не меняет общую логику дисперсионного анализа, а лишь несколько усложняет ее, поскольку, кроме учета влияния на зависимую переменную каждого из факторов по отдельности, следует оценивать и их совместное действие. Таким образом, то новое, что вносит в анализ данных многофакторный дисперсионный анализ, касается в основном возможности оценить межфакторное взаимодействие. Тем не менее, по-прежнему остается возможность оценивать влияние каждого фактора в отдельности. В этом смысле процедура многофакторного дисперсионного анализа (в варианте ее компьютерного использования) несомненно более экономична, поскольку всего за один запуск решает сразу две задачи: оценивается влияние каждого из факторов и их взаимодействие /3/.
Общая схема двухфакторного эксперимента, данные которого обрабатываются дисперсионным анализом имеет вид:
Рисунок 1.1 – Схема двухфакторного эксперимента
Данные, подвергаемые многофакторному дисперсионному анализу, часто обозначают в соответствии с количеством факторов и их уровней.
Предположив, что в рассматриваемой задаче о качестве различных m партий изделия изготавливались на разных t станках и требуется выяснить, имеются ли существенные различия в качестве изделий по каждому фактору:
А - партия изделий;
B - станок.
В результате получается переход к задаче двухфакторного дисперсионного анализа.
Все данные представлены в таблице 1.2, в которой по строкам - уровни Ai фактора А, по столбцам — уровни Bj фактора В, а в соответствующих ячейках, таблицы находятся значения показателя качества изделий xijk(i=1,2,...,m; j=1,2,...,l; k=1,2,...,n).
Таблица 1.2 – Показатели качества изделий
| B1 | B2 | … | Bj | … | Bl | |
| A1 | x11l,…,x11k | x12l,…,x12k | … | x1jl,…,x1jk | … | x1ll,…,x1lk |
| A2 | x21l,…,x21k | x22l,…,x22k | … | x2jl,…,x2jk | … | x2ll,…,x2lk |
| … | … | … | … | … | … | … |
| Ai | xi1l,…,xi1k | xi2l,…,xi2k | … | xijl,…,xijk | … | xjll,…,xjlk |
| … | … | … | … | … | … | … |
| Am | xm1l,…,xm1k | xm2l,…,xm2k | … | xmjl,…,xmjk | … | xmll,…,xmlk |
Двухфакторная дисперсионная модель имеет вид:
xijk=μ+Fi+Gj+Iij+εijk, (15)
где xijk - значение наблюдения в ячейке ij с номером k;
μ - общая средняя;
Fi- эффект, обусловленный влиянием i-го уровня фактора А;
Gj - эффект, обусловленный влиянием j-го уровня фактора В;
Iij - эффект, обусловленный взаимодействием двух факторов, т.е. отклонение от средней по наблюдениям в ячейке ij от суммы первых трех слагаемых в модели (15);
εijk - возмущение, обусловленное вариацией переменной внутри отдельной ячейки.
Предполагается, что εijk имеет нормальный закон распределения N(0; с2), а все математические ожидания F*,G*, Ii*, I*j равны нулю.
Групповые средние находятся по формулам:
- в ячейке:
,
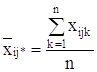по строке:
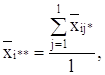
по столбцу:
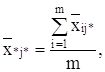
общая средняя:
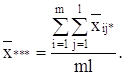
В таблице 1.3 представлен общий вид вычисления значений, с помощью дисперсионного анализа.
Таблица 1.3 – Базовая таблица дисперсионного анализа
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средние квадраты |
| Межгрупповая (фактор А) |
| m-1 |
|
| Межгрупповая (фактор B) |
| l-1 |
|
| Взаимодействие |
| (m-1)(l-1) |
|
| Остаточная |
| mln - ml |
|
| Общая |
| mln - 1 |
Проверка нулевых гипотез HA, HB, HAB об отсутствии влияния на рассматриваемую переменную факторов А, B и их взаимодействия AB осуществляется сравнением отношений 
, 
, 
(для модели I с фиксированными уровнями факторов) или отношений 
, 
, (для случайной модели II) с соответствующими табличными значениями F – критерия Фишера – Снедекора. Для смешанной модели III проверка гипотез относительно факторов с фиксированными уровнями производится также как и в модели II, а факторов со случайными уровнями – как в модели I.
Если n=1, т.е. при одном наблюдении в ячейке, то не все нулевые гипотезы могут быть проверены так как выпадает компонента Q3 из общей суммы квадратов отклонений, а с ней и средний квадрат 
, так как в этом случае не может быть речи о взаимодействии факторов.
С точки зрения техники вычислений для нахождения сумм квадратов Q1, Q2, Q3, Q4, Q целесообразнее использовать формулы:
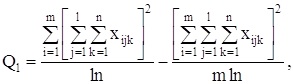
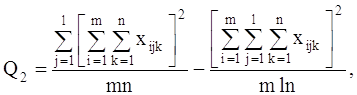
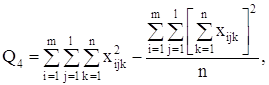
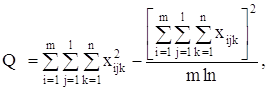
Q3 = Q – Q1 – Q2 – Q4.
Отклонение от основных предпосылок дисперсионного анализа — нормальности распределения исследуемой переменной и равенства дисперсий в ячейках (если оно не чрезмерное) — не сказывается существенно на результатах дисперсионного анализа при равном числе наблюдений в ячейках, но может быть очень чувствительно при неравном их числе. Кроме того, при неравном числе наблюдений в ячейках резко возрастает сложность аппарата дисперсионного анализа. Поэтому рекомендуется планировать схему с равным числом наблюдений в ячейках, а если встречаются недостающие данные, то возмещать их средними значениями других наблюдений в ячейках. При этом, однако, искусственно введенные недостающие данные не следует учитывать при подсчете числа степеней свободы /1/.
Похожие работы
... (от e) Общая m – число данных в строке (число повторов в ячейке), - число столбцов, - число строк. 3. Дисперсионный анализ в системе MINITAB Для проведения дисперсионного анализа в системе MINITAB необходимо выбрать из меню Stat > ANOVA. Различные возможности проведения дисперсионного анализа представлены следующими командами. ...
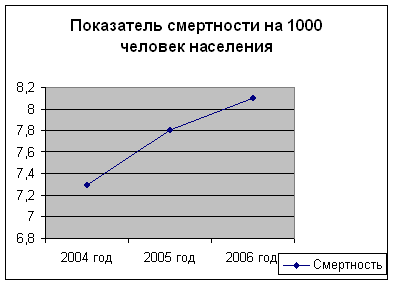
... отклика является смертность населения в конкретной возрастной группе, а факторами, влияющими на ее изменение, являются классы заболеваний. 2.2. Дисперсионный анализ Методом дисперсионного анализа, выясним, оказывает ли влияние различные заболевания на показатель смертности населения. То есть, проверим, выполняется ли гипотеза о равенстве математических ожиданий (Н0: М(Х1) = М(Х2) = … = ...
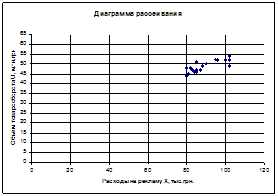
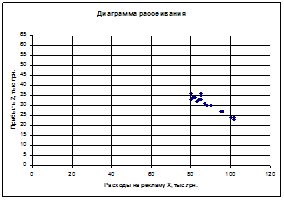
... товаров на рынок и объемом товарооборота предприятия торговли; Rxz = -0,96 корреляция расходами предприятия на рекламу и продвижение товаров на рынок и прибылью предприятия. Задача 2. Однофакторный дисперсионный анализ При уровне значимости a=0.05 определите статистическую достоверность влияния фактора А на динамику величины Х. № испытания A1 A2 A3 A4 1 2 2 6 7 ...
... можно предположить что при 5% уровне значимости ВАШСП не зависит от инфекции вызывающей реактивный артрит. В связи с тем что не один из показателей активности заболевания а также показатели ВАШ не зависят от инфекции предшествующей реактивному артриту дальнейшее разделение данных на группы можно считать не целесообразным. 2 Множественная линейная регрессия Общее назначение множественной ...
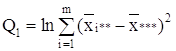
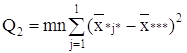
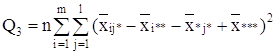
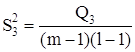
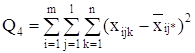
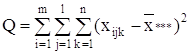
0 комментариев