Навигация
Существует ли в конечной группе порядка 8 подгруппа порядка 4
4. Существует ли в конечной группе порядка 8 подгруппа порядка 4.
Задние третьего уровня
1. Проверить, является ли множество рациональных чисел группой по сложению.
2.
Пусть Н – множество
перестановок
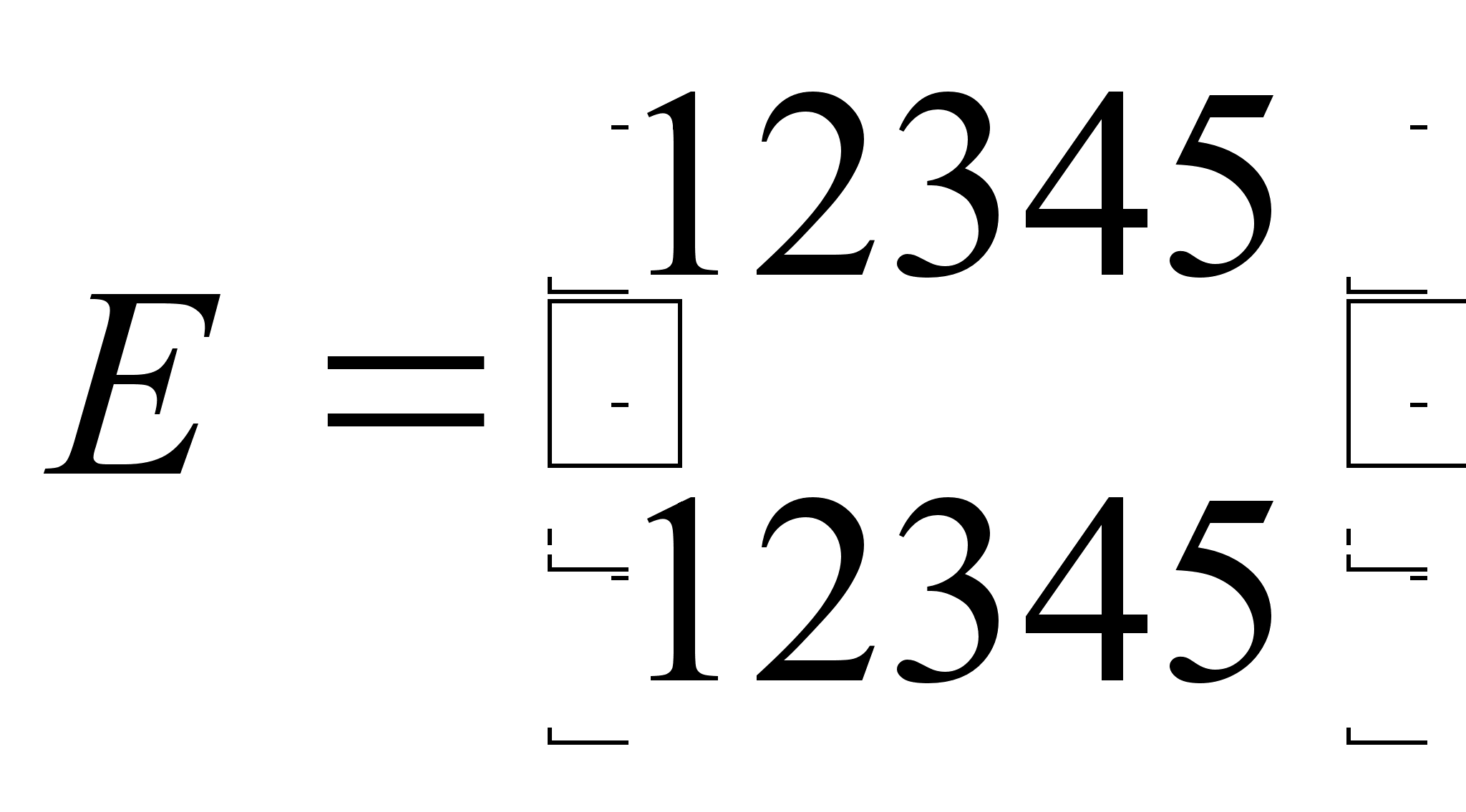 ,
,
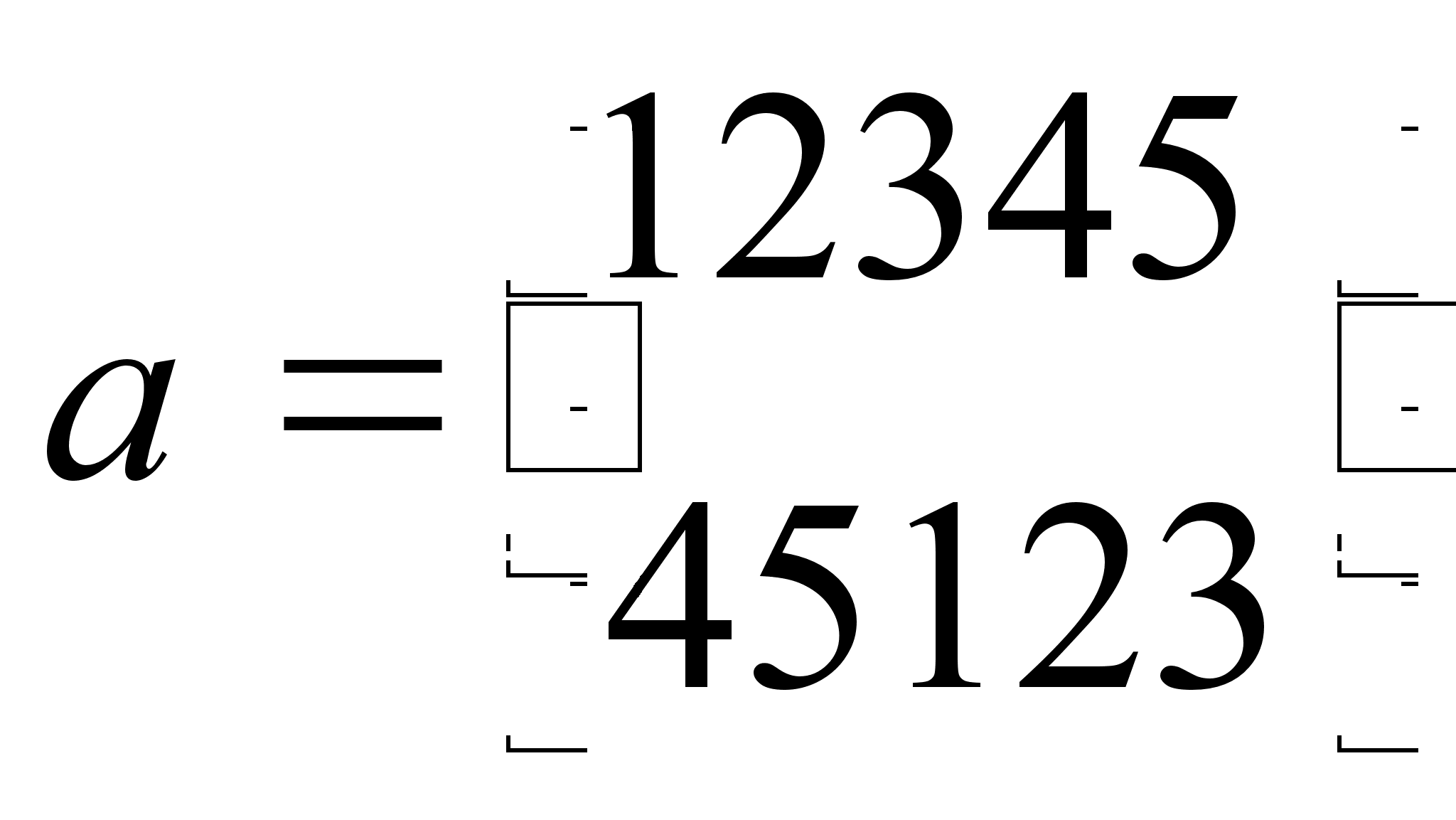 ,
,
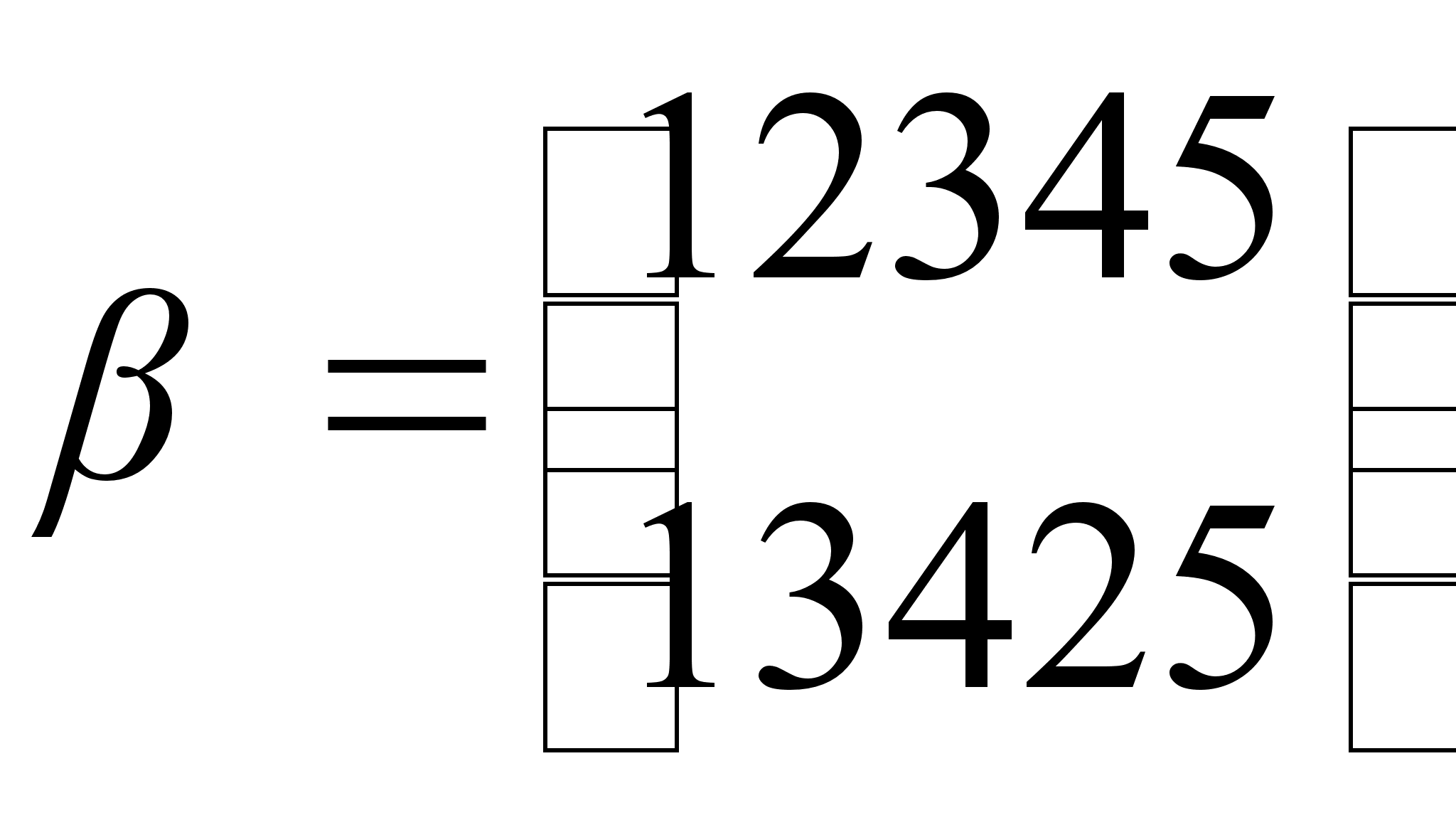 ,
,
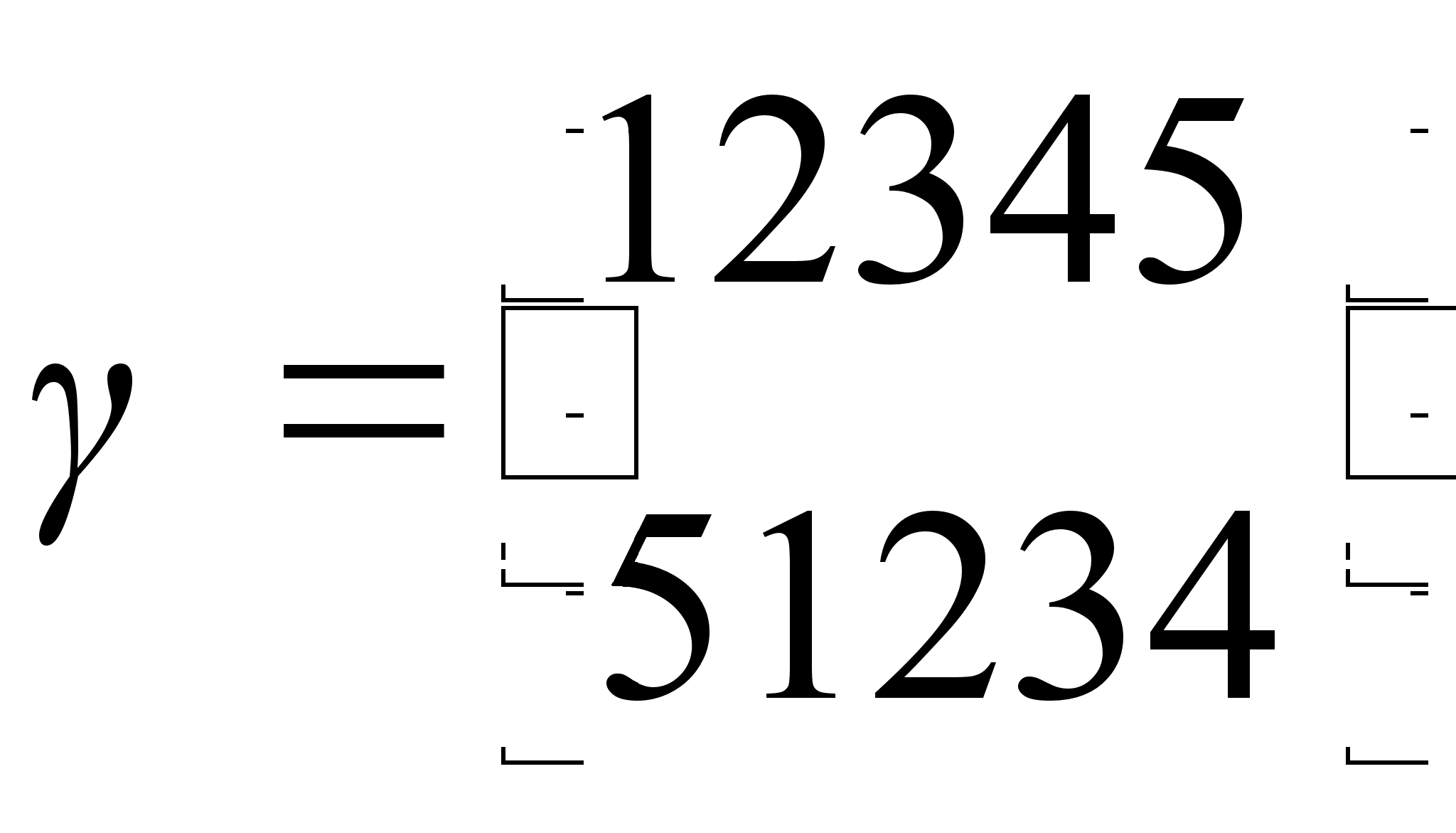 ,
,
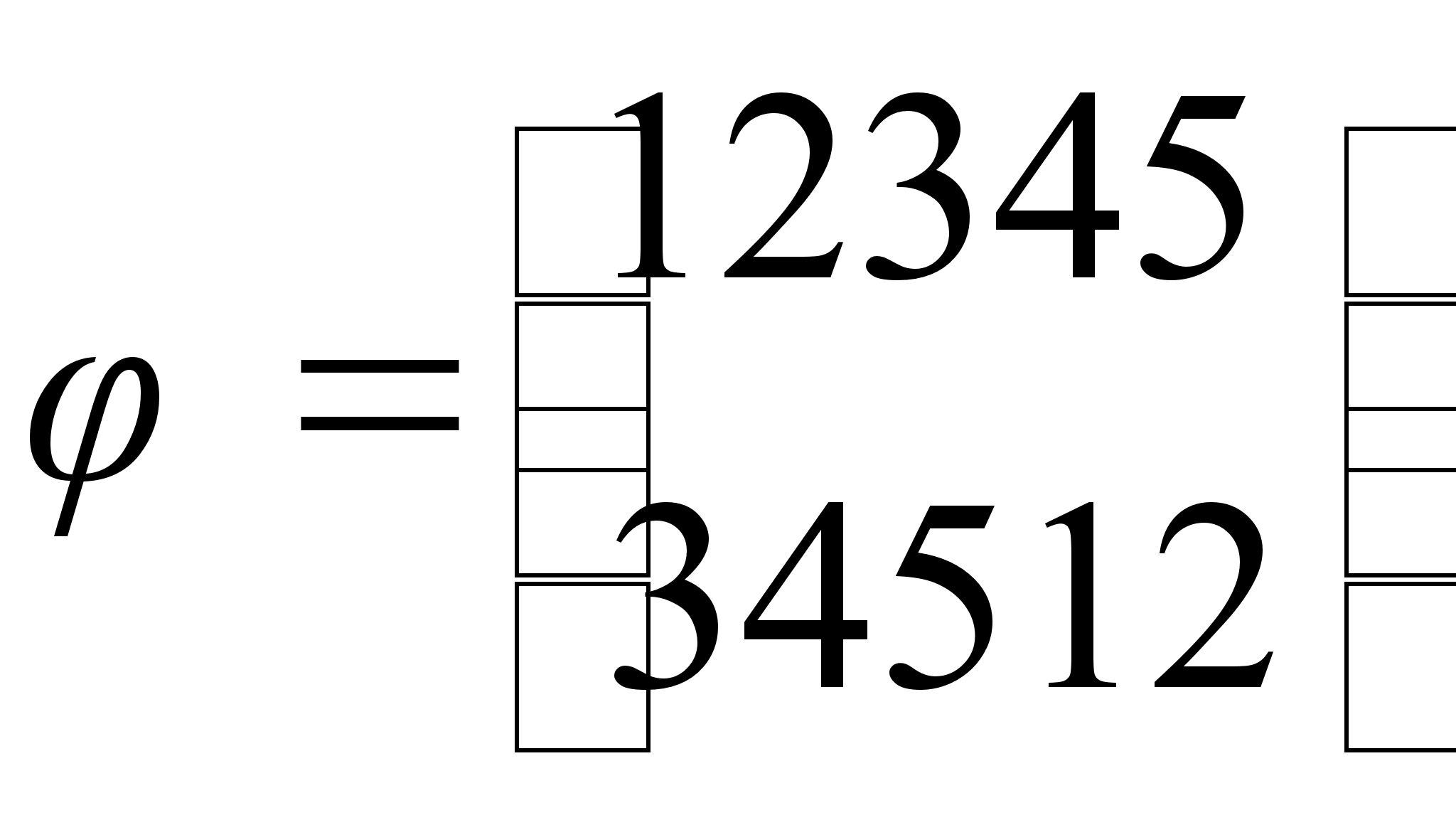 .
Проверить,
является ли
Н подгруппой
группы S5.
.
Проверить,
является ли
Н подгруппой
группы S5.
3.
Дана перестановка
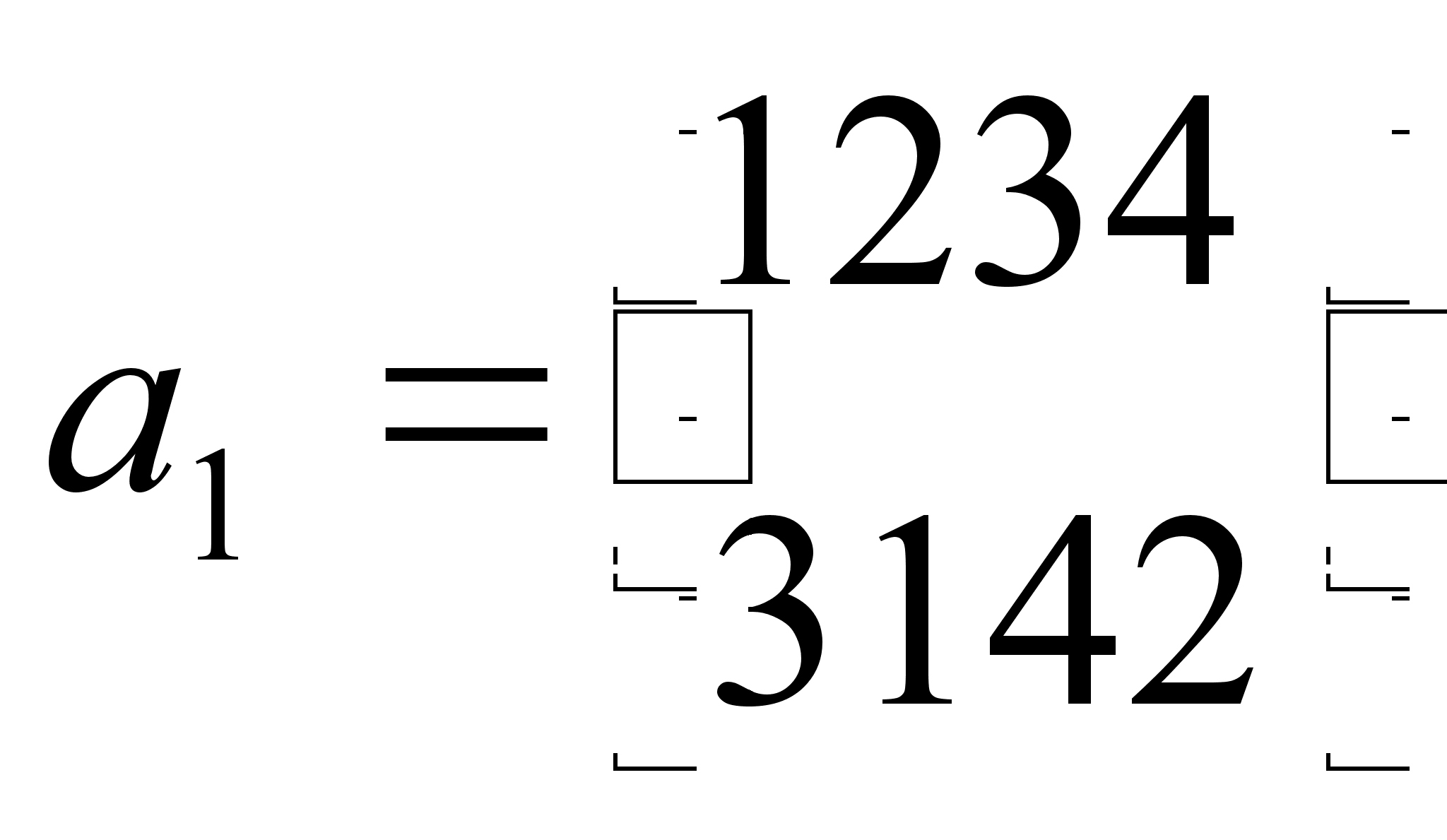 .
Найдите
.
Найдите ![]() ,
,
![]() ,
,
![]() и покажите, что
множество
и покажите, что
множество ![]() является группой
перестановок.
является группой
перестановок.
Задания четвертого уровня
1. Приведите пример четырехэлементной группы.
Приложение 3
Итоговая проверочная работа по материалу факультативного
курса «Элементы современной алгебры».
Задания первого уровня
1.
Заданы преобразования
![]() :
:
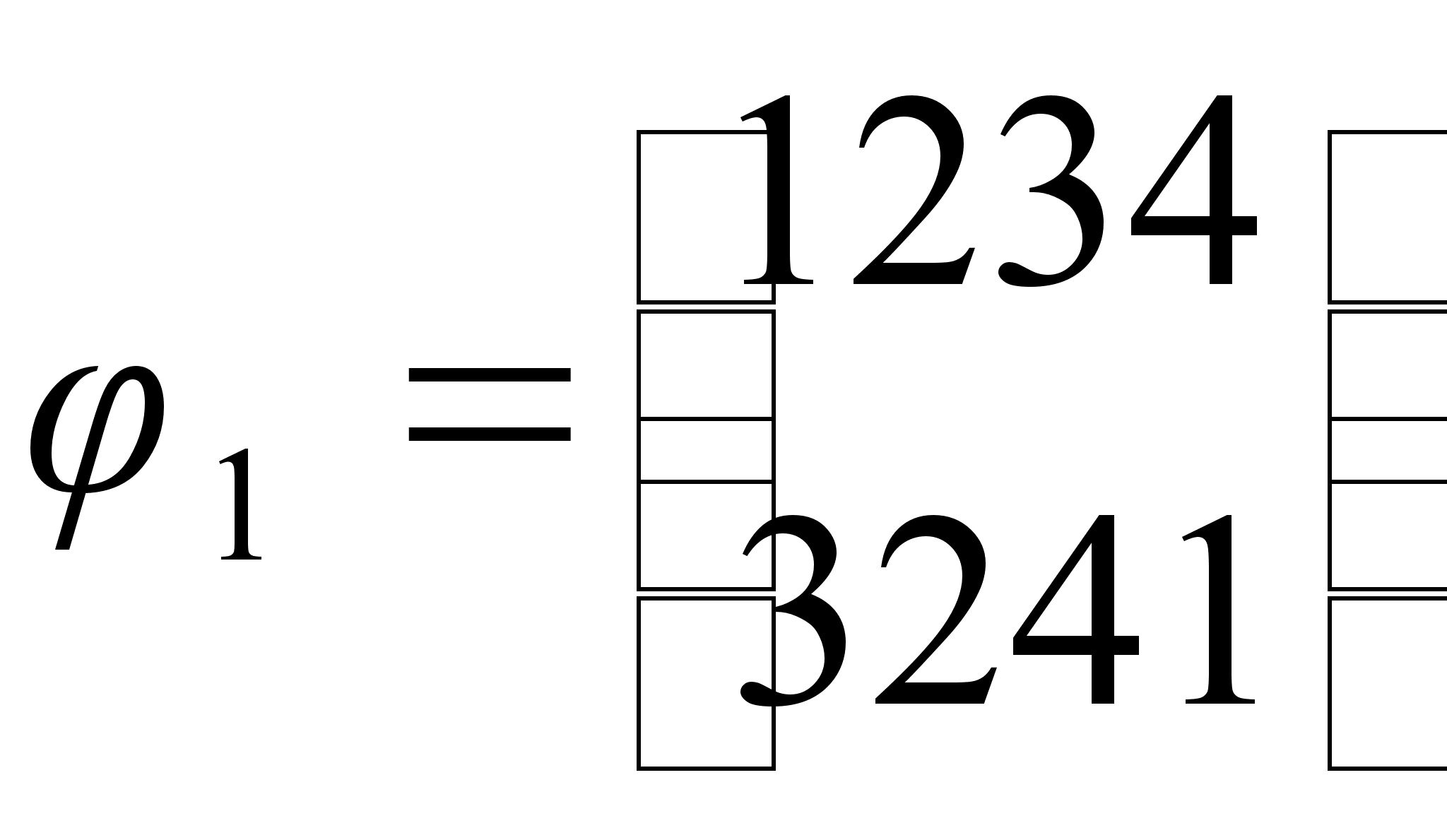 ,
,
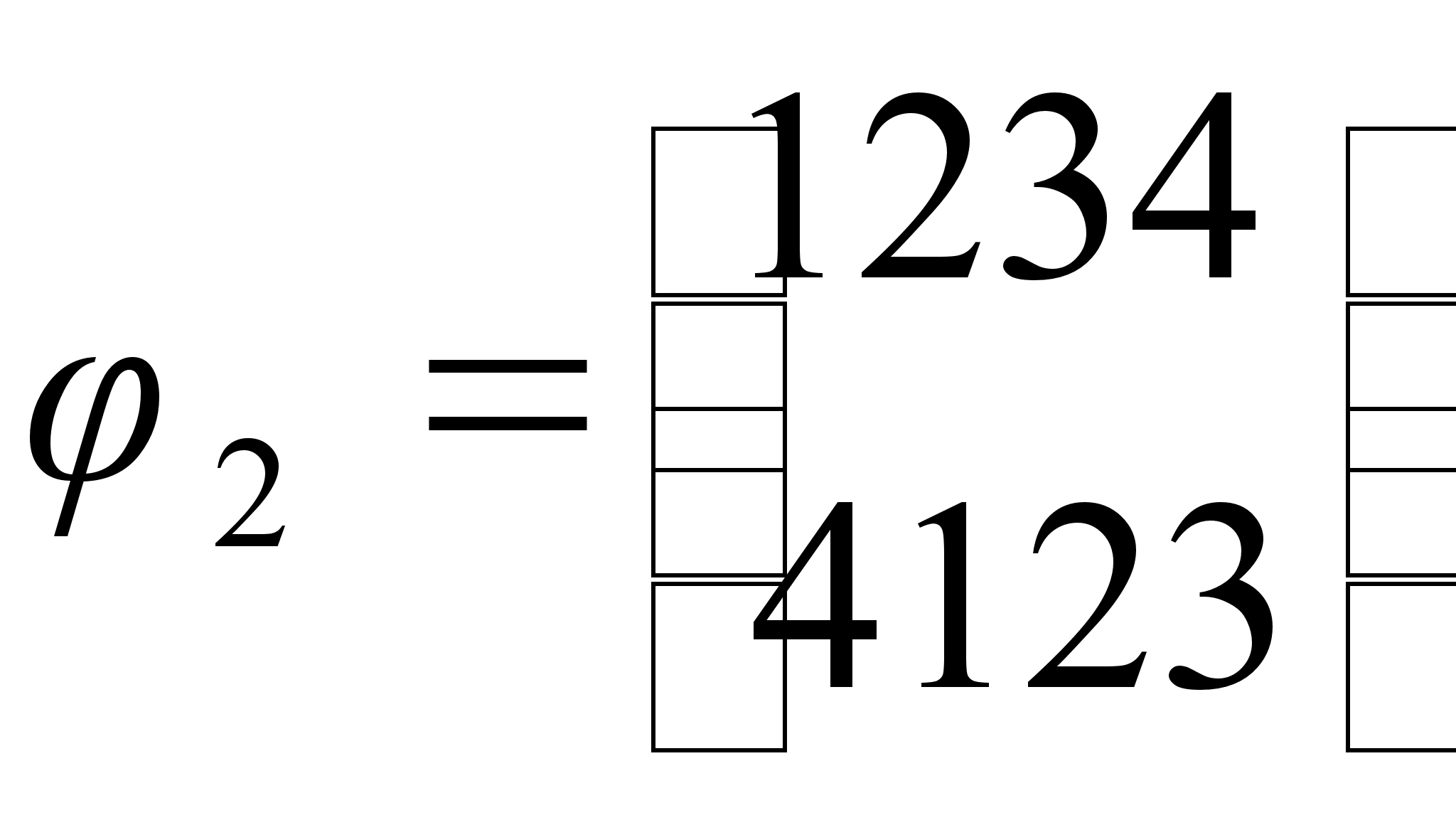 ,
,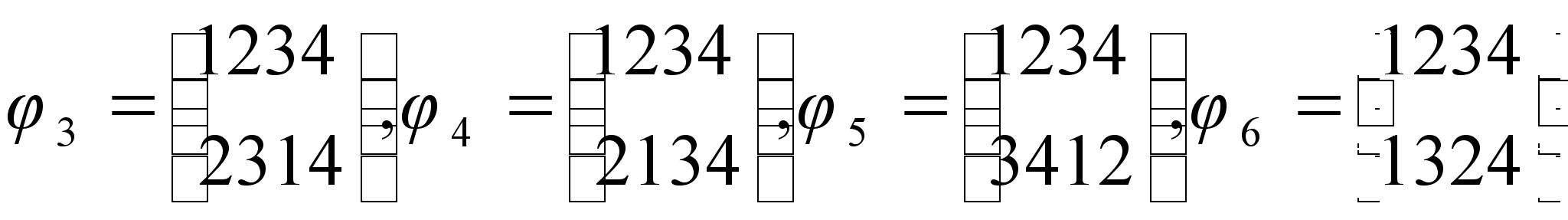 .
Среди преобразований
.
Среди преобразований
![]() укажите а)
укажите а) ![]() ,
б)
,
б) ![]() .
.
2. Является ли операция умножения алгебраической операцией на множестве действительных чисел.
3. Дана подгруппа , в ней нашелся элемент –5 такой, что выполняется соотношение: 5+(-5)+5=5. Является ли элемент 5 регулярным в подгруппе .
4.
![]() .
Из предложенных
ниже последовательностей
выберите те,
которые являются
словами над
алфавитом X.
.
Из предложенных
ниже последовательностей
выберите те,
которые являются
словами над
алфавитом X.
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
д)
![]() е)
е)
![]()
ж)
![]()
5.
В подгруппе выполнено
равенство ![]() .
Является ли
элемент b
правым делителем
элемента
.
Является ли
элемент b
правым делителем
элемента ![]() .
.
6. Пусть - группа, - группа. Является ли подгруппой группы . Обоснуйте ответ.
7. Какие из следующих преобразований являются перестановками:
а)
 б)
б)
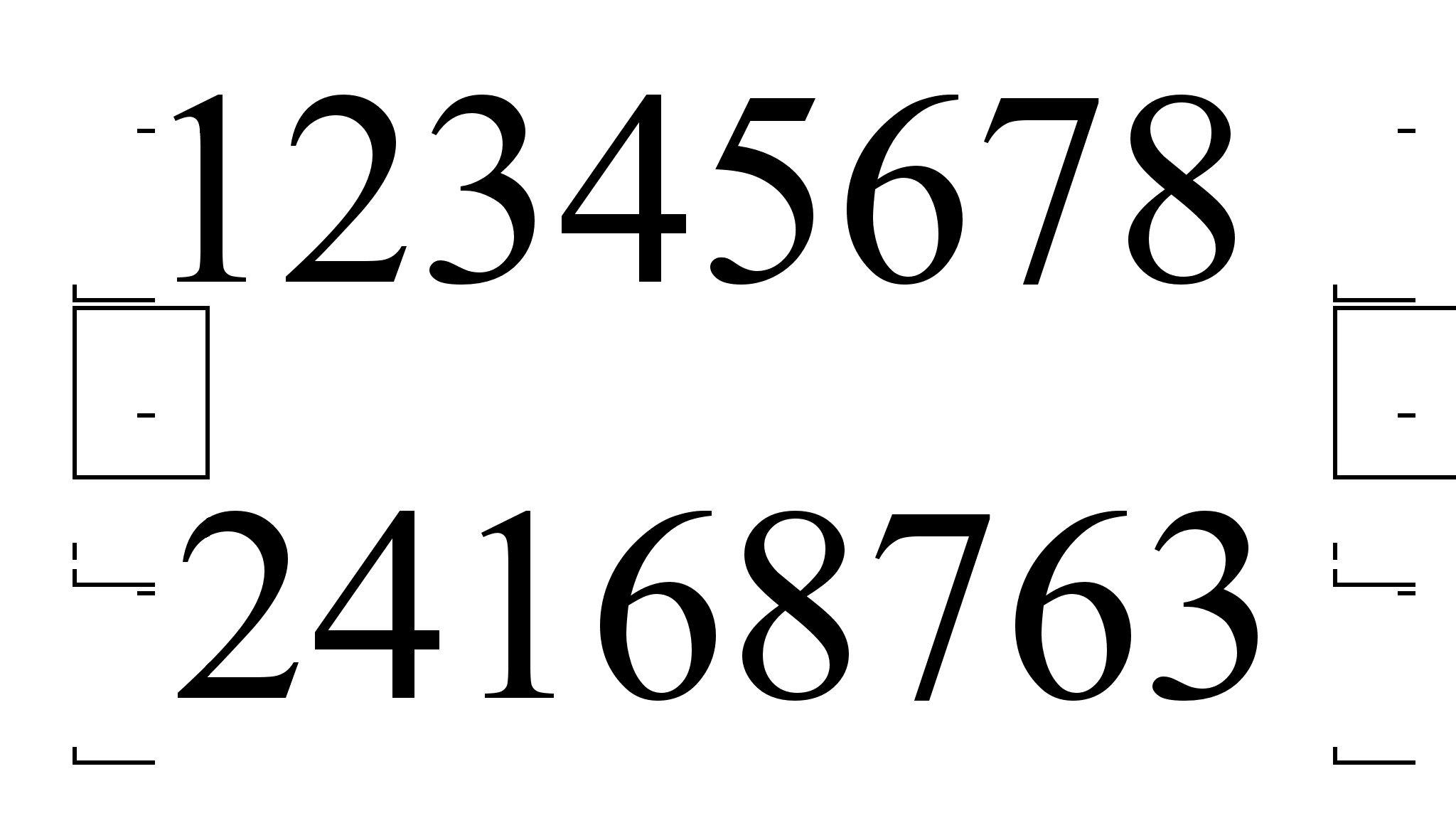
в)
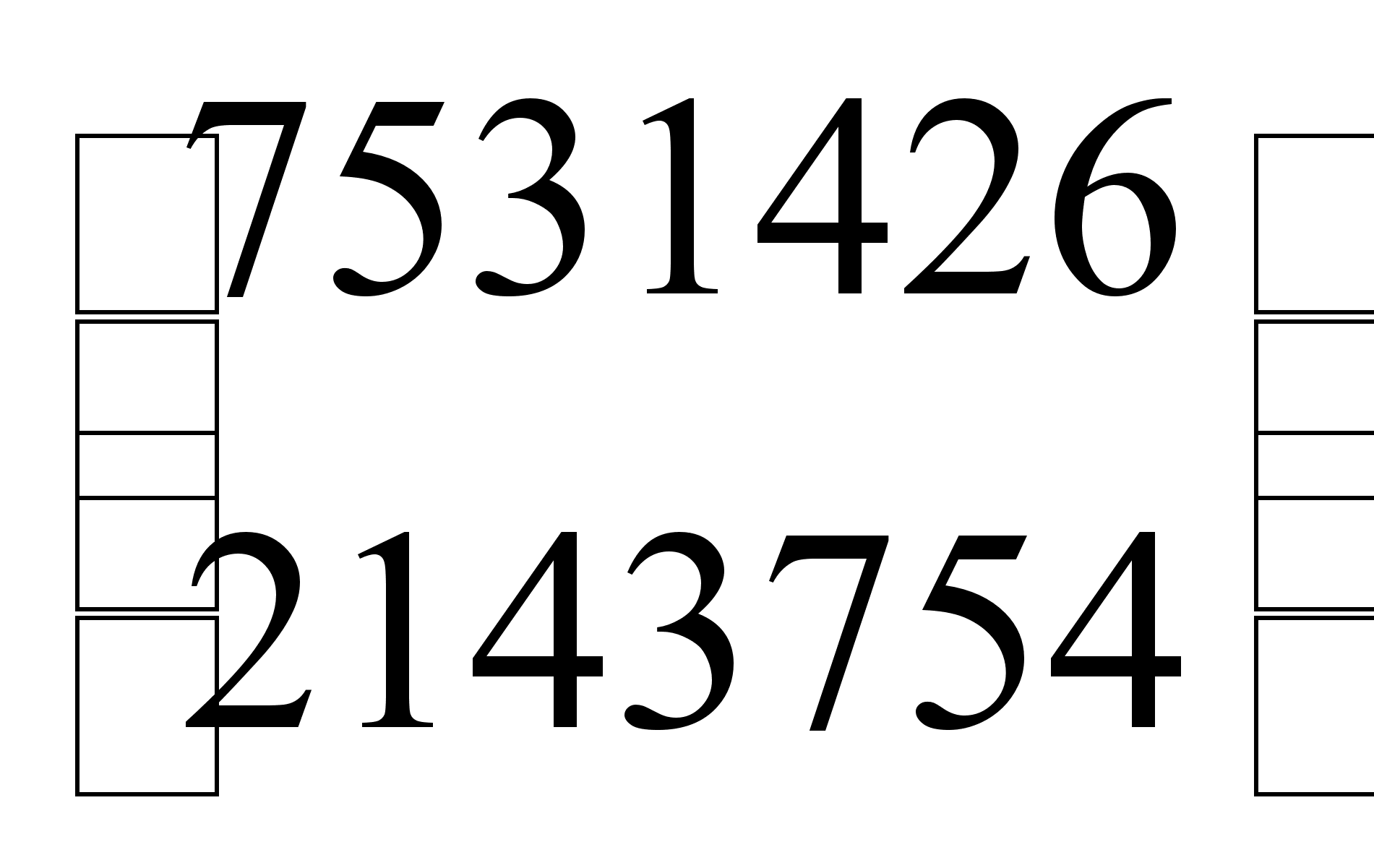 г)
г)
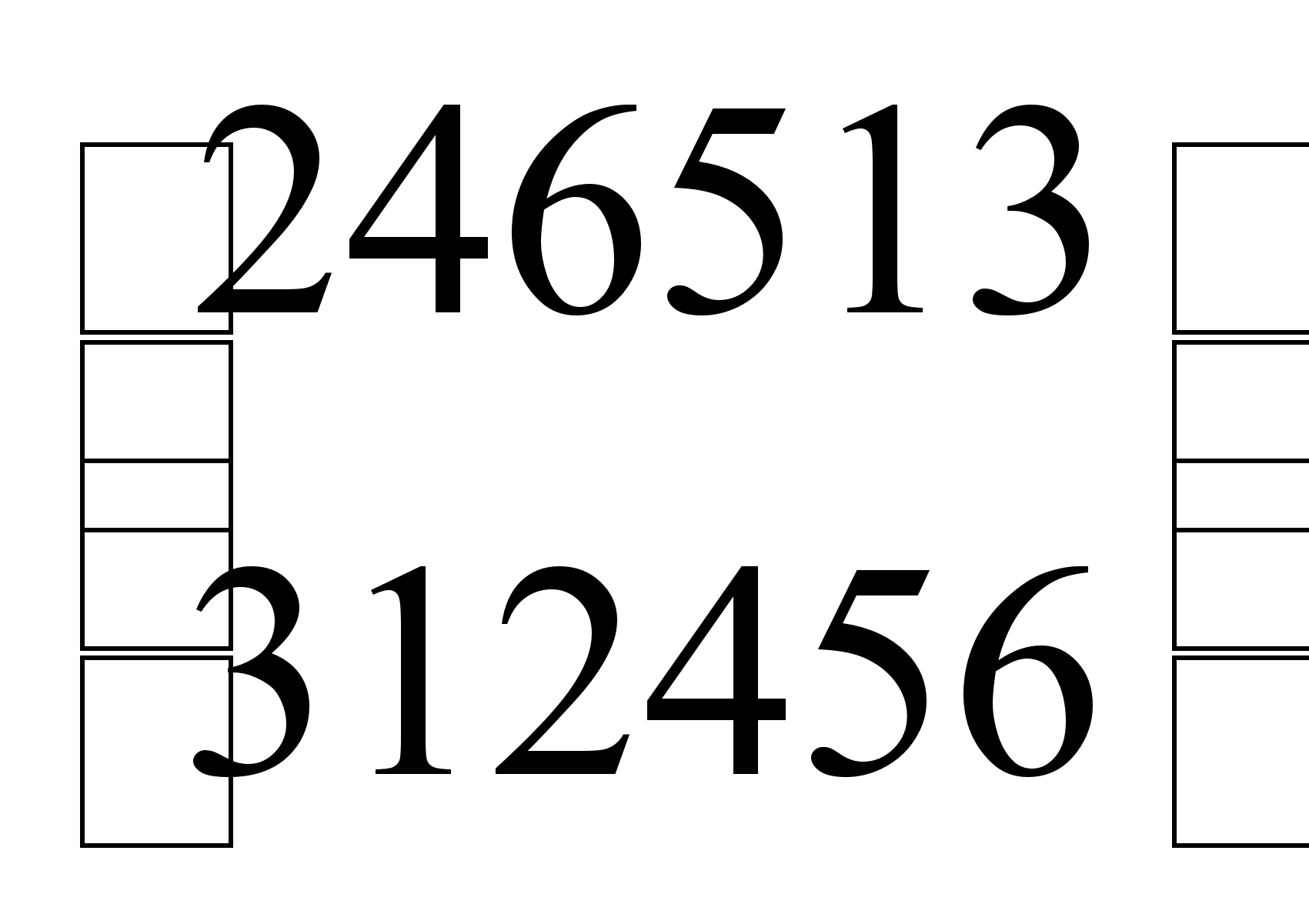 .
.
Задания второго уровня
1.
Множество ![]() ,
где
,
где 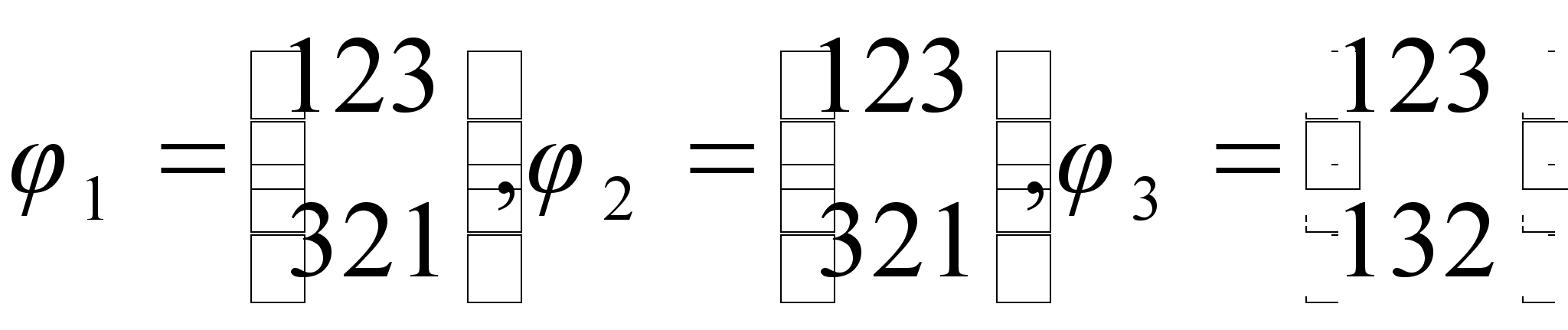 .
Образует ли
множество М
относительно
операции «*»
полугруппу.
.
Образует ли
множество М
относительно
операции «*»
полугруппу.
2. Из операций (+, -, *, /) укажите только те, которые являются алгебраическими в каждом из числовых множеств (N, Z, Q, R).
3. Дана полугруппа . Проверить, будет ли данная полугруппа регулярной.
4.
u,
v,
w
– слова над
алфавитом ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Из предложенных
ниже последовательностей
выберите те,
которые являются
словами, равными
u*(w*v),
(u*w)*v:
.
Из предложенных
ниже последовательностей
выберите те,
которые являются
словами, равными
u*(w*v),
(u*w)*v:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() .
.
5.
На множестве
![]() заданы произведения
u*v=E
и w*u=E,
u=x2x1
заданы произведения
u*v=E
и w*u=E,
u=x2x1![]() .
Найдите
слова v
и w,
удовлетворяющие
произведениям.
.
Найдите
слова v
и w,
удовлетворяющие
произведениям.
6.
Дано множество
![]() .
Являются ли
группами , где «+» операция
сложения и , где «*» операция
умножения.
.
Являются ли
группами , где «+» операция
сложения и , где «*» операция
умножения.
7.
Доказать, что
подмножество
![]() ,
где
,
где 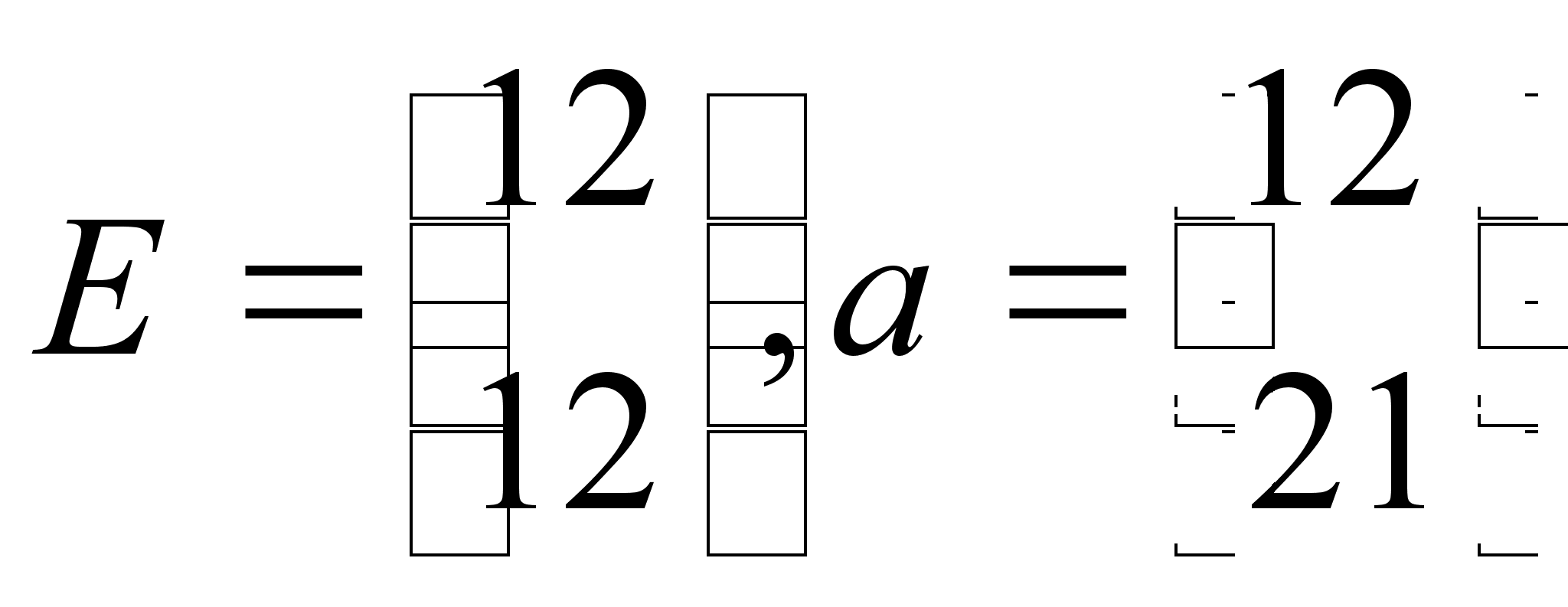 является подгруппой
группы S3.
является подгруппой
группы S3.
8.
Действия в
полугруппе
![]() задано таблицей
Кэли:
задано таблицей
Кэли:
| a | b | c | |
| a | a | b | c |
| b | a | b | c |
| c | a | b | c |
Верно ли утверждение, что каждый элемент подгруппы делится на каждый элемент из этой же полугруппы слева.
9.
Определите,
является ли
полугруппой
множество
, если ![]() .
.
10.
Решите уравнение:
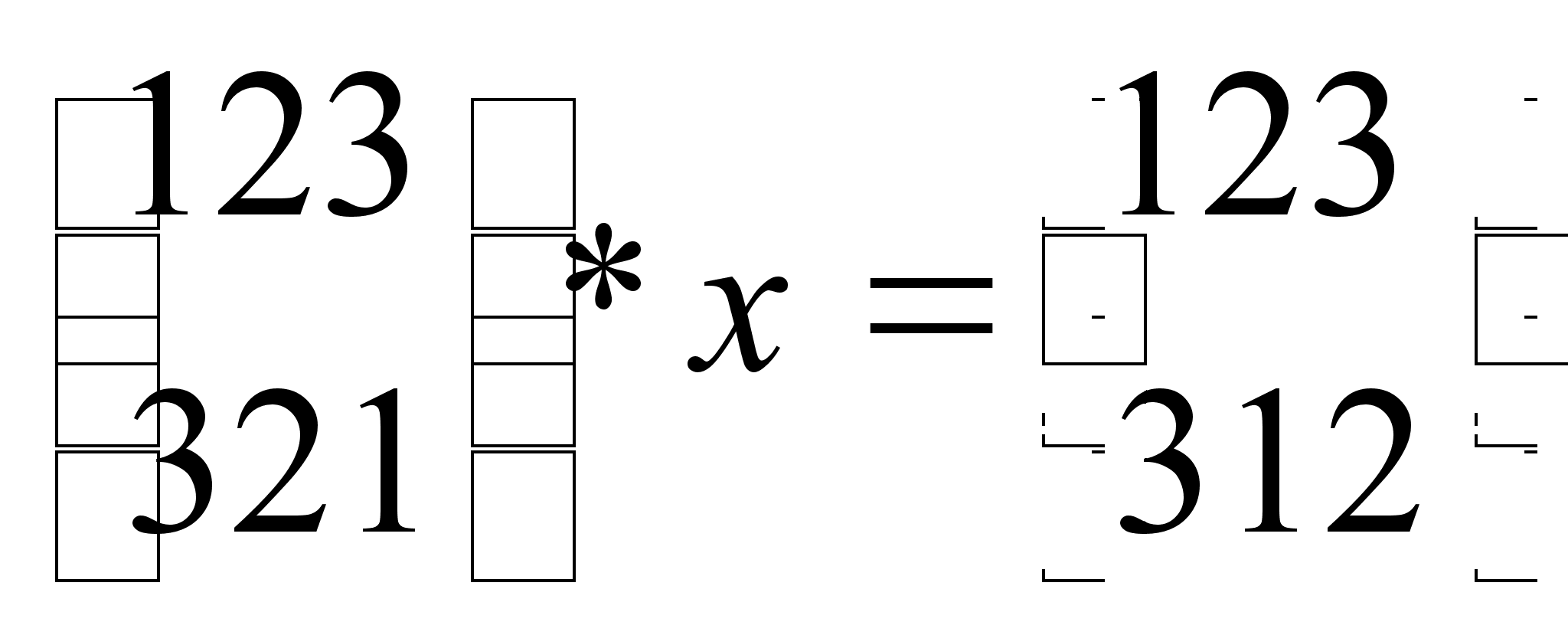 .
.
Задания третьего уровня
1. Всякая ли регулярная полугруппа является инверсной. Ответ обосновать.
2. Приведите пример полугруппы преобразований, состоящей из трех элементов.
3. Как вы думаете, будет ли свободная полугруппа свободной группой. Обоснуйте ответ.
4.
Пусть Н –множество
перестановок
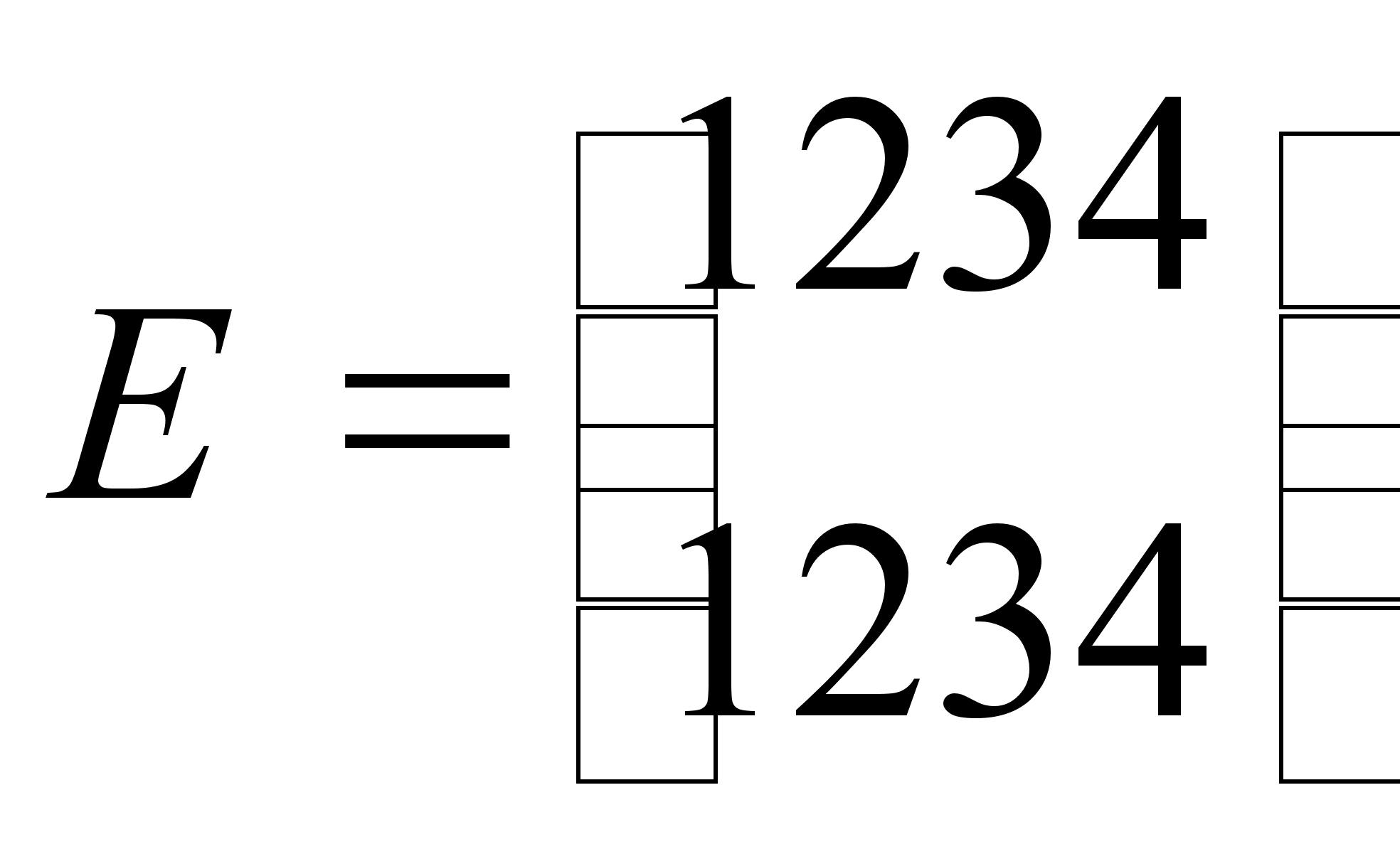 ,
,
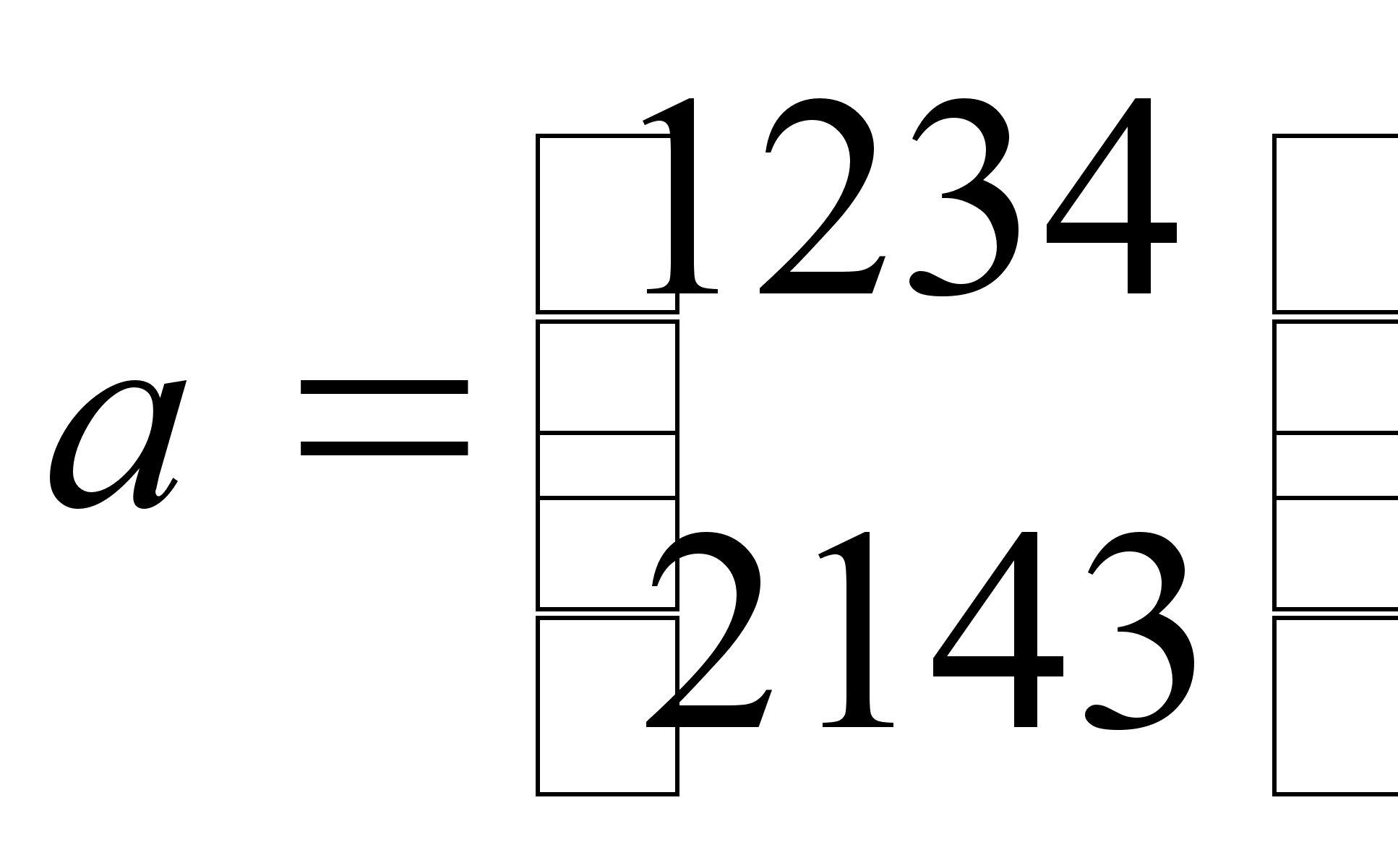 ,
,
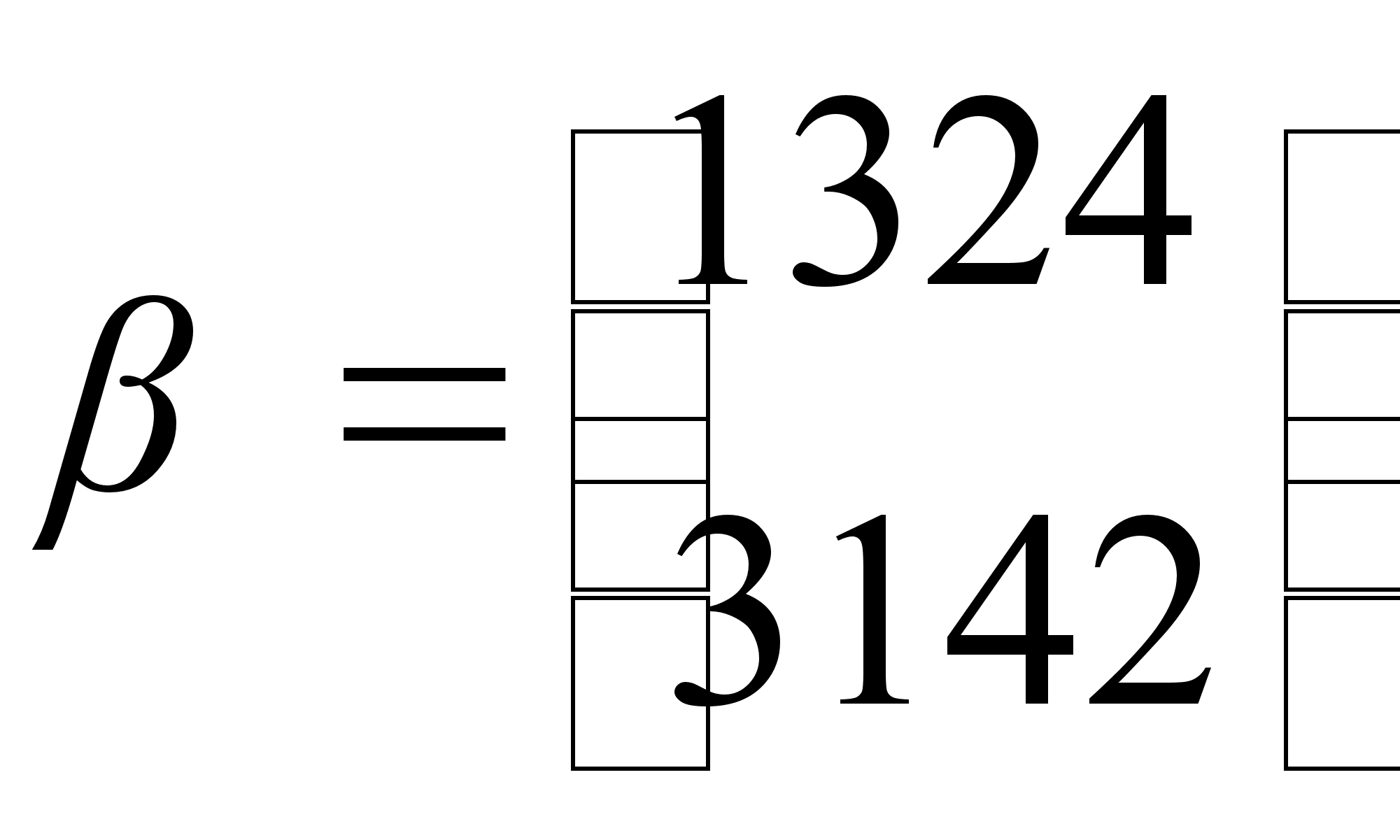 ,
,
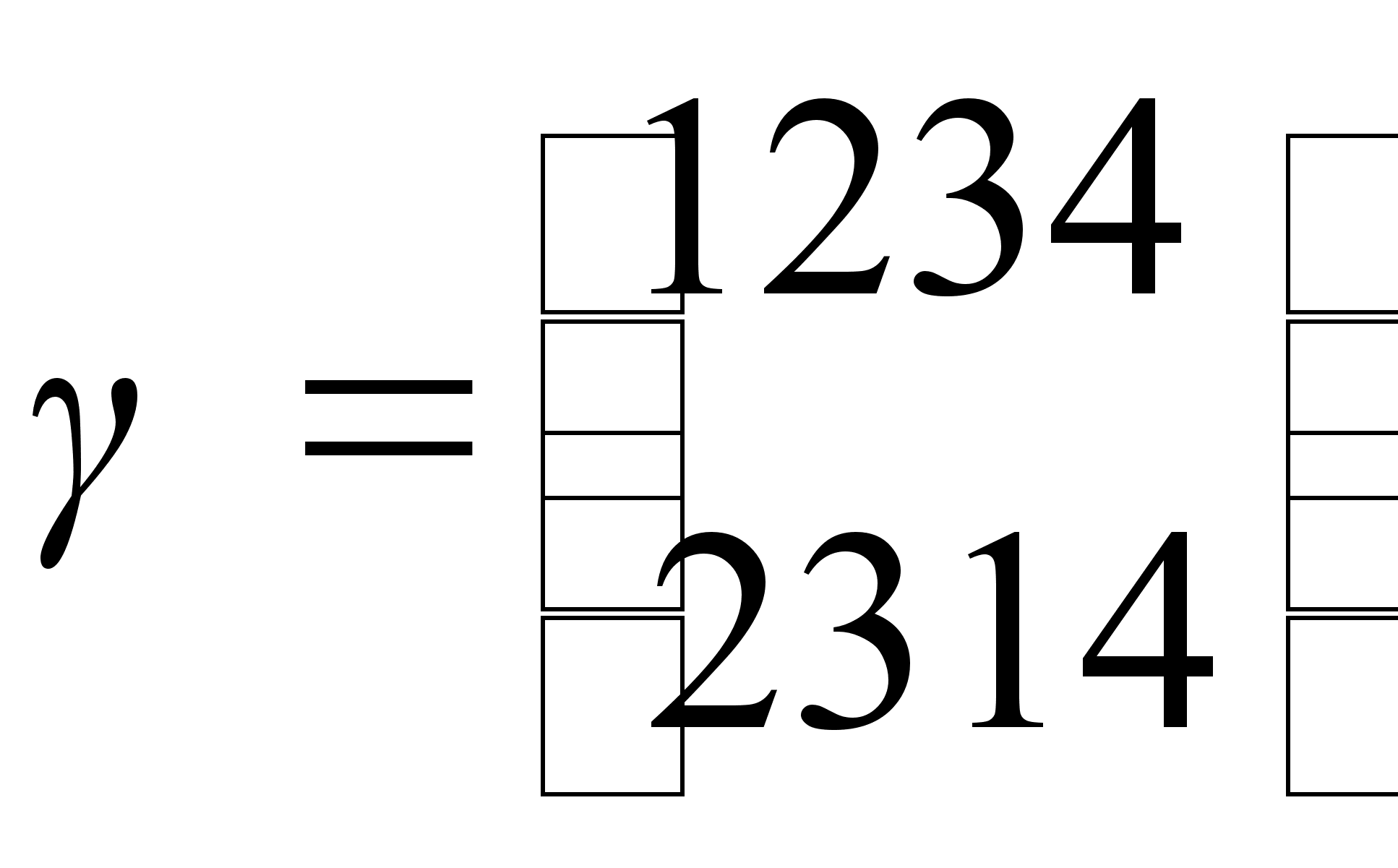 .
Проверьте,
является ли
Н подгруппой
группы S4.
.
Проверьте,
является ли
Н подгруппой
группы S4.
5.
Действие в
полугруппе
![]() задано таблицей
Кэли:
задано таблицей
Кэли:
| * | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
Что можно сказать о делимости элементов в полугруппе.
7.
Дана перестановка
u1=![]() .
Найдите
.
Найдите ![]() ,
,
![]() .
Покажите, что
множество
.
Покажите, что
множество ![]() является группой
перестановок
(по таблице
Кэли).
является группой
перестановок
(по таблице
Кэли).
8. Задайте во множестве R операцию *, по которой числа 2 и 3 можно поставить в соответствие число m и проверить, является ли полугруппой:
а)
m=2 б)
m=1 в)
m=![]() .
.
Задание четвертого уровня
1. Придумайте фигуру для которой можно составить группу симметрий, имеющей 4 элемент
0 комментариев