Навигация
Кривые третьего и четвертого порядка
24482
знака
2
таблицы
14
изображений
Чувашский государственный университет им. И.Н. Ульянова
Кафедра высшей математики
КУРСОВАЯ РАБОТА
на тему:
«Кривые третьего и четвертого порядка»
Выполнили: студенты
группы С-12-00
Пинаев И.Н.
Искаков Р.Р.
Проверила:
доцент кафедры высшей математики
к.ф.-м.наук Самарина С.М.
Чебоксары, 2002
Декартов лист
1. Особенности формы. Декартовым листом называется кривая 3-го порядка, уравнение которой в прямоугольной системе имеет вид
(1)
Иногда удобно пользоваться параметрическими уравнениями декартова листа, которые можно получить, полагая y=tx, присоединяя к этому равенству равенство (1) и решая полученную систему относительно х и у, в результате будем иметь:
|
| (2) |
откуда следует, что декартов лист является рациональной кривой.
Заметим еще, что полярное уравнение декартова листа имеет вид
(3)
Координаты х и у входят в уравнение декартова листа симметрично, откуда следует, что кривая симметрична относительно биссектрисы у=х. Обычное исследование на особые точки приводит к заключению, что начало координат является узловой точкой декартова листа. Уравнения касательных к алгебраической кривой в ее особой точке, совпадающей с началом координат, можно получить, как известно, приравнивая нулю группу членов низшей степени из уравнения этой кривой. В нашем случае имеем З аху = 0, откуда получим х = 0 и у = 0 – искомые уравнения касательных в узловой точке. Эти касательные совпадают с координатными осями и, следовательно, в начале координат кривая пересекает сама себя под прямым углом. Легко видеть, что в первом координатном угле кривая делает петлю, которая пересекается с прямой у = х в точке
Точки этой петли, в которых касательные параллельны координатным осям, имеют координаты
и 
(cм. рис. 1)
Для окончательного заключения о форме кривой следует еще найти асимптоту
Заменяя в уравнении кривой у на 
приравняем нулю в полученном уравнении коэффициенты двух членов с высшими степенями х. Получим 
и b = - а. Таким образом, декартов лист имеет асимптоту
у = — х — а; следовательно, во 2-м и 4-м координатных углах ветви декартова листа уходят в бесконечность.
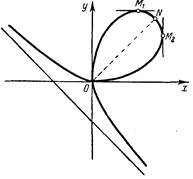
Рис. 1
2. Свойства. Согласно теореме Маклорена, если в трех точках алгебраической кривой 3-го порядка, лежащих на одной прямой, провести касательные к этой кривой, то точки их пересечения с кривой будут лежать также на прямой линии. Применительно к декартову листу эта теорема доказывается просто. Выведем с этой целью предварительно условие пребывания трех точек декартова листа, соответствующих значениям t1 , t2 и t3 параметра, на одной прямой. Если уравнение прямой имеет вид y=kx+b, то значения параметра, соответствующие точкам пересечения этой прямой с кривой, должны удовлетворять системе
Система эта приводит к уравнению
корни которого и будут искомыми значениями t1 , t2 и t3 параметра, откуда следует, что
(4)
Это равенство и является условием пребывания трех точек M1(t1 ), M2(t2), М3 (t3) декартова листа на одной прямой.
Располагая этим условием, покажем справедливость теоремы Маклорена для декартово листа. Действительно, касательную в точке M1 (t1) можно рассматривать как прямую, которая пересекает декартов лист в двух совпадающих между собой точках, для которых t2=t1, и в третьей точке, для которой соответствующее значение параметра обозначим через T1. Условие (4) примет вид t12 T1= -1. Для касательных в точках М2 и M3 получим аналогичные соотношения t22 T2 = -1 и t32 T3 = -1. Перемножая эти три равенства, будем иметь
(t1t2t3)2T1T2T3 = -1. откуда на основании (4) заключаем, что и T1T2T3 = -1, т. е. точки N1(T1), N2(T2) и N3(T3) лежат на одной прямой.
Определяя площадь, ограниченную петлей декартова листа, получим:
Похожие работы
... (0.5) в предположении, что коэффициенты кривых (0.4), (0.5) и системы (0.3) вещественные. Работа состоит из двух глав. В первой главе проводится построение квадратичной двумерной стационарной системы с частными интегралами в виде кривых третьего и первого порядков. При этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой тремя ...
помощью метода Рунге-Кутты четвертого порядка с автоматическим выбором шага на отрезке . Задачу можно решить аналитически, найдя решение дифференциального уравнения и подставив в него начальное условие, тем самым, отыскав требуемую интегральную кривую. Но для нас интерес представляет решение данной задачи с применением численного метода, а конкретнее – метода Рунге-Кутты 4-го порядка с ...
... при использовании этого метода функцию необходимо вычислять четыре раза. 3. Выбор метода реализации программы Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы выбираем наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений. этот метод является одноступенчатым и одношаговым требует ...
... при использовании этого метода функцию необходимо вычислять четыре раза3. Выбор метода реализации программы Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы выбираем наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений этот метод является одноступенчатым и одношаговым ...
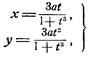
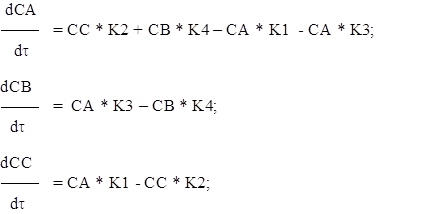
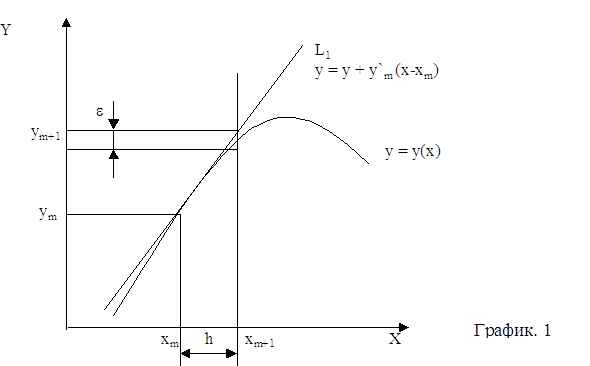
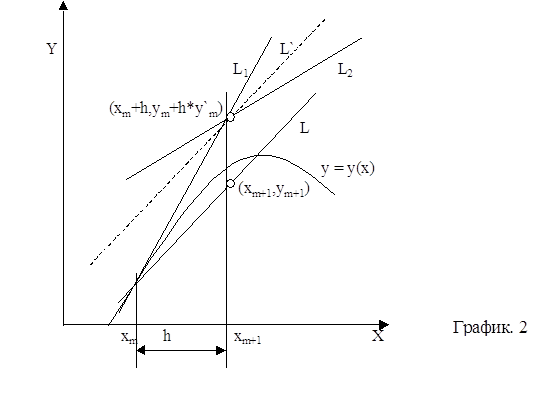
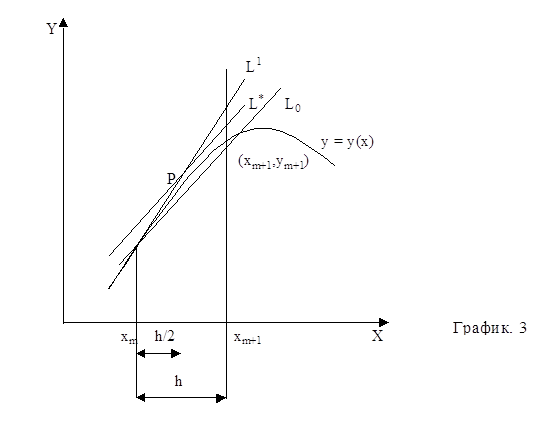
0 комментариев