Навигация
Натуральное уравнение кардиоиды получится, если из равенств (4) и (6) исключить параметр. Оно будет иметь вид
6. Натуральное уравнение кардиоиды получится, если из равенств (4) и (6) исключить параметр. Оно будет иметь вид
![]() (7)
(7)
7. Площадь, ограниченная кардиоидой, определится по формуле
![]()
и, как видно, равна ушестеренной площади производящего круга.
Длина всей кардиоиды определится по формуле
![]()
и, как видно, равна восьми диаметрам производящего круга. Объем тела, полученного от вращения кардиоиды вокруг ее оси, равен ![]()
Поверхность тела, полученного от вращения кардиоиды вокруг ее оси, равняется ![]()
Мы видели, что кардиоида органически связана с окружностью. Она является конхоидой круга и эпициклоидой. Она имеет с окружностью и иной характер родства — кардиоида является подэрой окружности относительно точки, принадлежащей этой окружности.
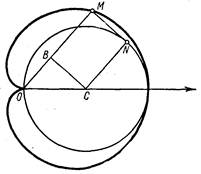
Рис.9
Действительно, пусть ОМ есть перпендикуляр, опущенный на касательную к окружности с радиусом, равным 2r, проведенную в точке N.
Так как ОМ = OB + ВМ, или r == 2r cos j + 2r, то геометрическим местом точек М будет кардиоида с уравнением r = 2r (1 + cos j).
Заметим в заключение, что кардиоида относится также к семейству синусоидальных спиралей, и отдельные свойства ее повторяют общие свойства этих кривых. Из этих свойств следует, в частности, что инверсия кардиоиды, относительно точки возврата дает параболу.
Астроида
1. Свойства. Астроида, как и рассмотренная выше кривая Штейнера, является частным случаем гипоциклоид, а именно, гипоциклоидой с модулем m, равным 1/4. Она представляет собой, следовательно, траекторию точки, лежащей на окружности круга радиуса r, который катится по внутренней стороне другого, неподвижного круга, радиус R которого в четыре раза больше.
Параметрические уравнения астроиды можно получить, полагая в уравнениях гипоциклоиды, m=1/4. Вот эти уравнения:
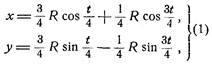
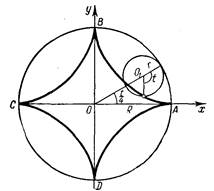
Рис. 10
где t, как и ранее, угол поворота производящего круга (рис. 10)
Исключая из уравнений (1) параметр t, получим:
![]() (2)
(2)
Из уравнения (2) следует, что астроида является алгебраической кривой 6-го порядка.
Параметрические уравнения (1) астроиды можно привести к виду
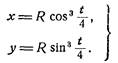 (3)
(3)
Исключая из этих уравнений параметр t, получим часто употребляемый вид уравнения астроиды
![]() (4)
(4)
Полагая в ранее выведенных общих соотношениях для циклоидальных кривых модуль
m = -1/4, получим соответствующие соотношения для астроиды:
1) радиус кривизны в произвольной точке астроиды определяется по формуле
![]() (5)
(5)
2) длина дуги астроиды от точки А до произвольной точки M(t) определится по формуле
![]() (6)
(6)
длина одной ветви равна ![]() а длина всей кривой 6R;
а длина всей кривой 6R;
3) для получения натурального уравнения астроиды заметим предварительно, что если началом отсчета длины дуги полагать не точку А, для которой t = 0, а точку, для которой t = p, то длина дуги определится формулой
![]() (6)
(6)
исключая параметр t из уравнений (5) и (6), получим натуральное уравнение астроиды
![]()
4) эволюта астроиды есть также астроида, подобная данной, с коэффициентом подобия, равным 2, повернутая относительно данной на угол p/4 (рис.11)
5) площадь, ограниченная всей астроидой, равна ![]() объем тела, полученного от вращения астроиды, равняется 32/105p R3
объем тела, полученного от вращения астроиды, равняется 32/105p R3
поверхность тела, образованного вращением астроиды, равна ![]()
Обратимся теперь к рассмотрению некоторых частных свойств астроиды.
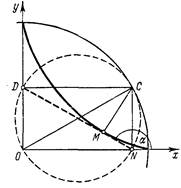
Астроида является огибающей отрезка постоянной длины, концы. которого скользят по двум взаимно перпендикулярным прямым.
Принимаем эти прямые за оси координат и, обозначая угол наклона скользящего отрезка ND=R через a (рис.12), будем иметь уравнение прямой ND в виде
![]() (7)
(7)
Дифференцируя это уравнение по параметру a, получим:
![]()
Исключая из последнего уравнения и уравнения (7) параметр a, будем иметь уравнение огибающей в виде ![]() т. е. астроиду.
т. е. астроиду.
Практически перемещение отрезка ND можно осуществить с помощью так называемых кардановых кругов. Один из этих кругов с радиусом R неподвижен, а другой, с радиусом r, в два раза меньшим, катится по внутренней стороне неподвижного круга. Любые две диаметрально противоположные точки N и D катящегося круга будут перемещаться по двум взаимно перпендикулярным диаметрам Ох и Оу неподвижного круга. Ясно, что огибающей диаметра катящегося круга и будет астроида.
|
Рис. 11 |
Рис. 12 |
Рассмотренный способ образования астроиды можно истолковать также следующим образом. Прямоугольник ODCN, две стороны которого лежат на двух взаимно перпендикулярных прямых, деформируется так, что диагональ его сохраняет длину, равную R, огибающая диагонали и будет астроидой. Так как при этом перпендикуляр, опущенный из вершины С на диагональ DN, служит нормалью к огибающей, то астроида представляет собой геометрическое место оснований перпендикуляров, опущенных из вершины С прямоугольника на его диагональ.
2. Свойства касательных к астроиде. Уравнение (7) выражает прямую ND, т. е. касательную к астроиде в некоторой точке М, причем параметр a представляет собой угол, составляемый этой касательной с осью абсцисс. Уравнение другой касательной, перпендикулярной к первой, будет иметь вид
![]() (8)
(8)
Исключая из уравнений (7) и (8) параметр а, получим уравнение ![]() или, в полярной системе,
или, в полярной системе, ![]() которое выражает четырехлепестковую розу. Итак, геометрическое место вершин прямого угла, стороны которого касаются астроиды, есть четырех лепестковая роза.
которое выражает четырехлепестковую розу. Итак, геометрическое место вершин прямого угла, стороны которого касаются астроиды, есть четырех лепестковая роза.
Другое свойство касательных к астроиде таково: каждая касательная пересекает астроиду в двух точках, касательные в которых пересекаются в точке, лежащей на окружности описанного около астроиды круга.
Определим подэру астроиды относительно точки Р, лежащей на биссектрисе 1-го координатного угла на расстоянии ОР=с от начала координат. Выше было показано, что астроиду можно рассматривать как огибающую отрезка ND = R, скользящего своими концами по координатным осям. Отсюда
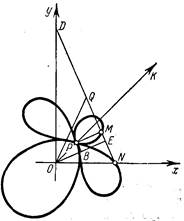
Рис. 13
следует, что искомую подэру можно определить как геометрическое место оснований перпендикуляров, опущенных из точки Р на прямую ND (рис. 13). Проведем ОЕ _|_ ND, и OQ, где Q — середина отрезка ND. Точку Р посчитаем полюсом, а прямую РК полярной осью. Полярный угол КРМ точки М подэры обозначим через j, а радиус-вектор РМ — через r. Тогда, как легко видеть, угол ![]()
Так как ![]()
Но, с другой стороны, ![]() На основании последних двух равенств, полярное уравнение подэры запишется в виде
На основании последних двух равенств, полярное уравнение подэры запишется в виде ![]() а в прямоугольной системе с началом в точке Р в виде
а в прямоугольной системе с началом в точке Р в виде
![]()
Полученная таким образом кривая 6-го порядка имеет в начале координат четырехкратную точку и называется «жуком». В частном случае, пои с=0, жук становится розой,
3. Косая астроида. Обобщением рассмотренной астроиды является так называемая косая астроида, которая представляет собой огибающую отрезка ND постоянной длины R, скользящего своими концами по двум прямым, пересекающимся под произвольным углом f.
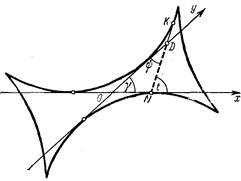
Рис. 14
Полагая эти пересекающиеся прямые координатными осями, обозначим угол, составляемый прямой ND с осью абсцисс, через t. Тогда из треугольника OND (рис. 14) будем иметь:
![]()
откуда
![]()
и следовательно, уравнение прямой ND в отрезках на осях запишется в виде
![]()
Дифференцируя это уравнение по t и исключая из полученного после дифференцирования равенства и уравнения прямой параметр t, получим параметрические уравнения косой астроиды в виде
![]()
при ![]() эти уравнения выражают рассмотренную ранее прямую астроиду.
эти уравнения выражают рассмотренную ранее прямую астроиду.
Похожие работы
... (0.5) в предположении, что коэффициенты кривых (0.4), (0.5) и системы (0.3) вещественные. Работа состоит из двух глав. В первой главе проводится построение квадратичной двумерной стационарной системы с частными интегралами в виде кривых третьего и первого порядков. При этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой тремя ...
помощью метода Рунге-Кутты четвертого порядка с автоматическим выбором шага на отрезке . Задачу можно решить аналитически, найдя решение дифференциального уравнения и подставив в него начальное условие, тем самым, отыскав требуемую интегральную кривую. Но для нас интерес представляет решение данной задачи с применением численного метода, а конкретнее – метода Рунге-Кутты 4-го порядка с ...
... при использовании этого метода функцию необходимо вычислять четыре раза. 3. Выбор метода реализации программы Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы выбираем наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений. этот метод является одноступенчатым и одношаговым требует ...
... при использовании этого метода функцию необходимо вычислять четыре раза3. Выбор метода реализации программы Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы выбираем наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений этот метод является одноступенчатым и одношаговым ...
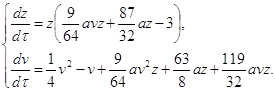
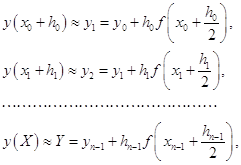
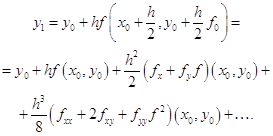
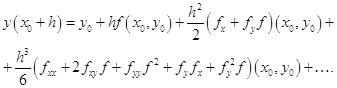
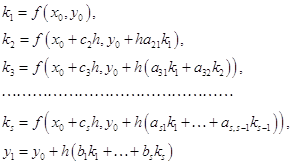
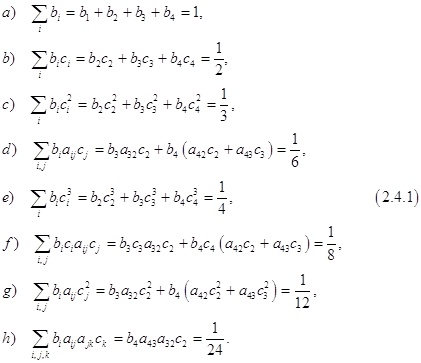
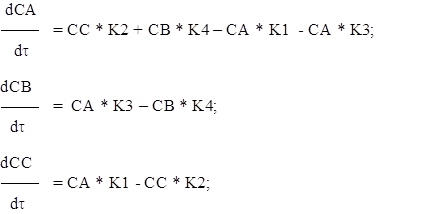
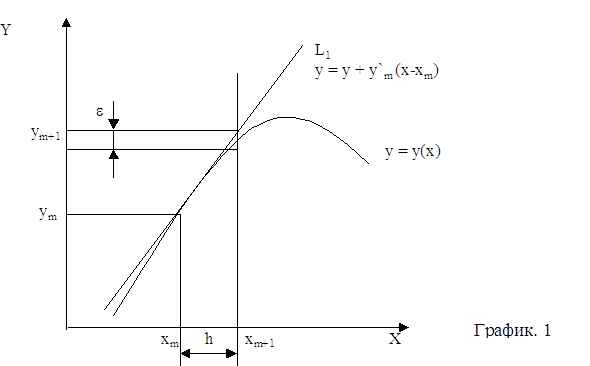

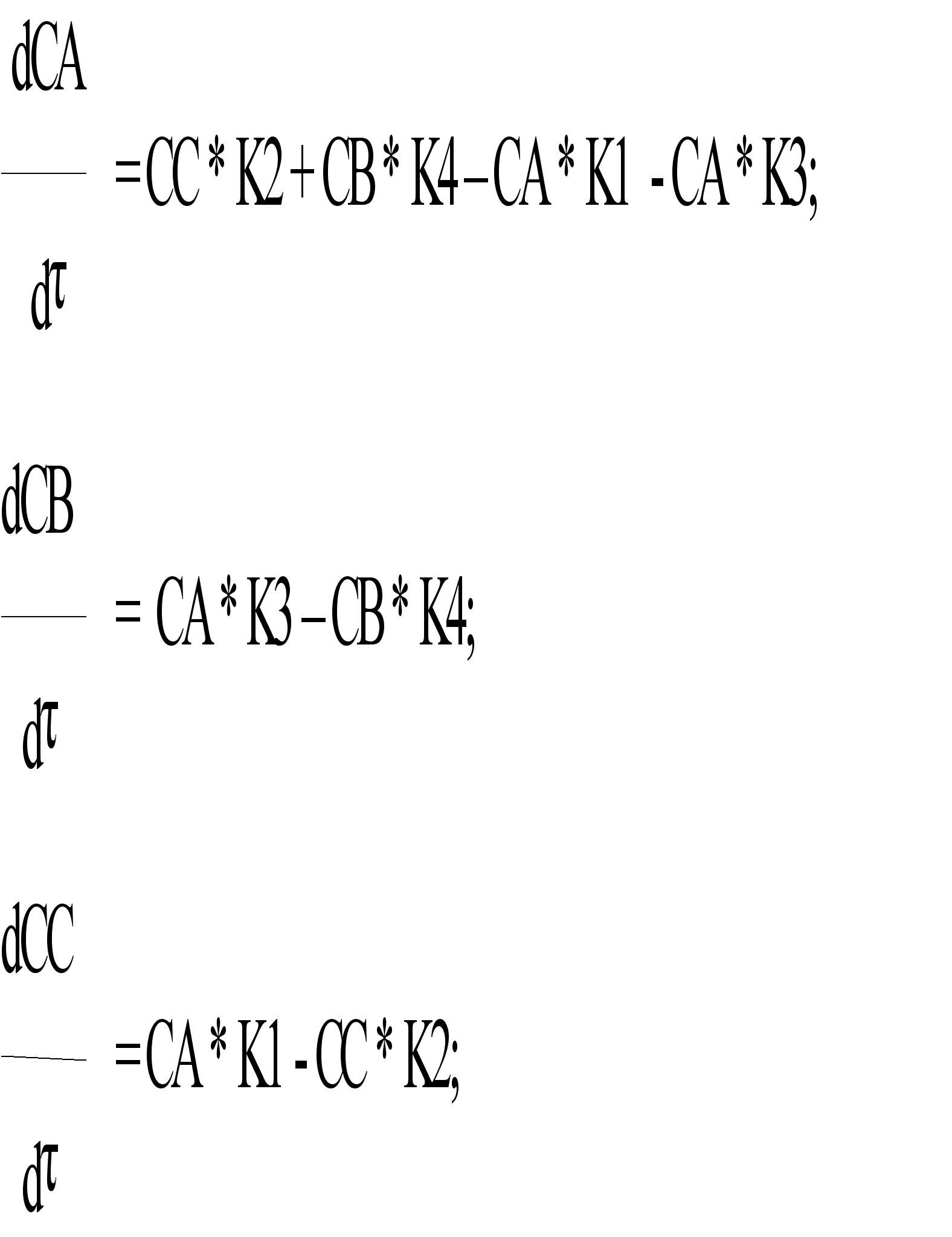

0 комментариев