Навигация
Примеры задач, решаемых графическим методом
2.1. Примеры задач, решаемых графическим методом.
Решим графическим методом задачи использования сырья и составления рациона.
Задача использования сырья. Для изготовления двух видов продукции Р1 и Р2 используют три вида сырья: S1, S2, S3. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукци, а так же величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 2.1.
Таблица 2.1.
| Вид сырья | Запас сырья | Количество единиц сырья, идущих на изготовление единицы продукции | |
| Р1 | Р2 | ||
| S1 | 20 | 2 | 5 |
| S2 | 40 | 8 | 5 |
| S3 | 30 | 5 | 6 |
| Прибыль от единицы продукции, руб. | 50 | 40 | |
Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
Решение.
Обозначим через х1 количество единиц продукции Р1, а через х2 – количество единиц продукции Р2. Тогда, учитывая количество единиц сырья, расходуемое на изготовление продукции, а так же запасы сырья, получим систему ограничений:
2х1 + 5х2 20
8х1 + 5х2 40
5х1 + 6х2 30
которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысит имеющихся запасов. Если продукция Р1 не выпускается, то х1=0; в противном случае x1 0. То же самое получаем и для продукции Р2. Таким образом, на неизвестные х1 и х2 должно быть наложено ограничение неотрицательности: х1 0, х2 0.
Конечную цель решаемой задачи – получение максимальной прибылипри реализации продукции – выразим как функцию двух переменных х1 и х2. Реализация х1 единиц продукции Р1 и х2 единиц продукции Р2 дает соответственно 50х1 и 40х2 руб. прибыли, суммарная прибыль Z = 50х1 + 40х2 (руб.)
Условиями не оговорена неделимость единица продукции, поэтому х1 и х2 (план выпуска продукции) могут быть и дробными числами.
Требуется найти такие х1 и х2, при которых функция Z достинает максимум, т.е. найти максимальное значение линейной функции Z = 50х1 + 40х2 при ограничениях
2х1 + 5х2 20
8х1 + 5х2 40
5х1 + 6х2 30
х1 0, х2 0.
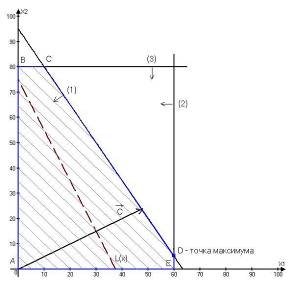
Построим многоугольник решений (рис. 2.3).
Для этого в системе координат х1Ох2 на плоскости на плоскости изобразим граничные прямые
2х1 + 5х2 = 20 (L1)
8х1 + 5х2 = 40 (L2)
5х1 + 6х2 = 30 (L3)
х1 = 0, х2 = 0.
Взяв какую-нибудь точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство (эти полуплоскости на рис. 2.3 показаны стрелками). Многоугольником решений данной задачи является ограниченный пятиугольник ОАВСD.
Для построения прямой 50х1 + 40х2 = 0 строим радиус-вектор N = (50;40) = 10(5;4) и через точку O проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора N. Из риc. 2.3 следует, что опорной по отношению к многоугольнику решений эта прямая становится в точке С, где функция Z принимает максимальное значение. Точка С лежит на пересечении прямых L1 и L2. Для определения ее координат решим систему уравнений
 8x1 + 5х2 = 40
8x1 + 5х2 = 40
5х1 + 6х2 = 30
Оптимальный план задачи: х1 = 90/23 = 3,9; х2 = 40/23 = 1,7. Подставляя значения х1 и х2 в линейную функцию, получаем Zmax = 50 3,9 + 40 1,7 = 260,3
Таким образом, для того чтобы получить максимальную прибыль в размере 260,3 руб., необходимо запланировать производство 3,9 ед. продукции Р1 и 1,7 ед. продукции Р2.
Задача составления рациона. При откорме каждое животное ежедневно должно получать не менее 9 ед. питательного вещества S1, не менее 8 ед. вещества S2 и не менее 12 ед. вещества S3. Для составления рациона используют два вида корма. Содержание количества елиниц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведены в таблице 2.2.
Таблица 2.2.
| Питательные вещества | Количество единиц питательных веществ в 1 кг корма. | |
| Корм 1 | Корм 2 | |
| S1 | 3 | 1 |
| S2 | 1 | 2 |
| S3 | 1 | 6 |
| Стоимость 1 кг корма, коп. | 4 | 6 |
Необходимо составить дневной рацион нужной питательности, причем затраты на него должны быть минимальными.
Решение.
Для составления математической модели обозначим через х1 и х2 соответственно количество килограммов корма 1 и 2 в дневном рационе. Принимая во внимание значения, приведенные в таблице 2.2, и условие, что дневной рацион удовлетворяет требуемой питательности только в случае, если количество единиц питательных веществ не меньше предусмотренного, получаем систему ограничений
3х1 + х2 9
х1 + 2х2 8
х1 + 6х2 12
х1 0, х2 0.
Если корм 1 не используется в рационе, то х1=0; в противном случае x1 0. Аналогично имеем х2 0. То есть должно выполняться условие неотрицательности переменных: х1 0, х2 0.
Цель данной задачи – добиться минимальных затрат на дневной рацион, поэтому общую стоимость рациона можно выразить в виде линейной функции Z = 4х1 + 6х2 (коп.)
Требуется найти такие х1 и х2, при которых функция Z принимает минимальное. Таким образом, необходимо найти минимальное значение линейной функции Z = 4х1 + 6х2 при ограничениях
3х1 + х2 9
х1 + 2х2 8
х1 + 6х2 12
х1 0, х2 0.
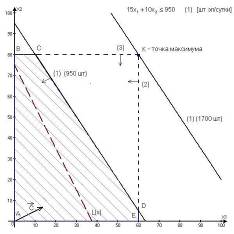
Построим многоугольник решений (рис. 2.4). Для этого в системе координат х1Ох2 на плоскости изобразим граничные прямые
3х1 + х2 = 9 (L1)
х1 + 2х2 = 8 (L2)
х1 + 6х2 = 12 (L3)
х1 = 0, х2 = 0.
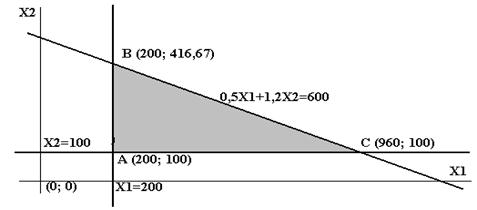
Взяв какую-нибудь точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство (эти полуплоскости на рис. 2.4 показаны стрелками). В результате получим неограниченную многоугольную область с угловыми точками А, В, С, D.
Для построения прямой 4х1 + 6х2 = 0 строим радиус-вектор N = (4;6) и через точку O проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора N. Из риc. 2.4 следует, она впервые коснется многогранника решений и станет опорной по отношению к нему в угловой точе В. Если прямую перемещать дальше в направлении вектора N, то значения линейной функции на многограннике решений возрастут, значит, в точке В линейная функция Z принимает минимальное значение.
Точка В лежит на пересечении прямых L1 и L2. Для определения ее координат решим систему уравнений
3x1 + х2 = 9
х1 + 2х2 = 8
Имеем: х1 = 2; х2 = 3. Подставляя значения х1 и х2 в линейную функцию, получаем Zmin = 4 2 + 6 3 = 26.
Таким образом, для того, чтобы обеспечить минимум затрат (26 коп. в день), необходимо дневной рацион составить из 2 кг корма 1 и 3 кг корма 2.
Похожие работы
... ячеек свидетельствует о том, что возможно лучшее решение и наоборот, если отрицательных ячеек нет, то было найдено оптимальное решение. 2. Содержательная постановка задачи Частным случаем задачи линейного программирования является транспортная задача. Проблема транспортировки включает поиск низко затратных схем распределения товарных запасов от многих источников до многих мест назначения ...
... игр, теория массового обслуживания, и др. 1. ПОСТАНОВКА ЗАДАЧИ Целью нашего курсового проекта является решение задачи линейного программирования графическим методом. 1.1 Математическое программирование. Математическое программирование ("планирование") – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ...
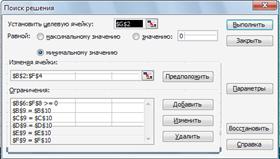
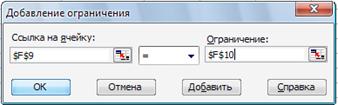
... с помощью двухэтапного метода, совпадает с решением, полученным в среде MS Excel с помощью программной надстройки «Поиск решения». 7. ПРИМЕРЫ ПОСТАНОВОК, ФОРМАЛИЗАЦИИ И РЕШЕНИЯ ПЕРСПЕКТИВНЫХ ОПТИМИЗАЦИОННЫХ УПРАВЛЕНЧЕСКИХ ЗАДАЧ Одним из методов решения задач линейного программирования является графический метод, применяемый для решения тех задач, в которых имеются только две переменные, ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
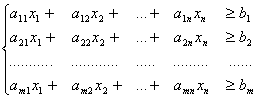





0 комментариев