Навигация
1.Счетные и несчетные множества. Счетность множества рациональных чисел.
Множество - совокупность некоторых объектов
Элементы множества - объекты составляющие множество
Числовые множества - множества элементами которых являются числа.
Задать множество значит указать все его элементы:
1 Способ: А={а: Р(а)} эти записи Читать- множество тех а таких что...
A={а-Р(а)} равноценны
Р(а) - предикат = высказывание об элементе, бывает ложно или истинно по отношению к кокретному элементу. Множество А состоит из тех а для которых предикат истина.
2 Способ: Конструирование из других множеств:
AB = {c: cA cB}, AB = {c: cA cB}, A\ B = {c: cA сB}
U - универсальное множество (фиксированное)
UA; U \ A = A’ = cA (A’ - дополнение множества A)
Свойства:
1. A(BC)=(AB)C - ассоциативность; AB=BA - коммутативность; A=A; AU=U
2. A (BC)=(AB)(AC) & A (BC)=(AB)(AC) - дистрибутивность; А=А
A” =A - закон исключающий третьего (AB)’=A’B’; (AB)’=A’B’; AA’=
Иллюстрация свойств: Диаграммы Эйлера-Венна.
"=>" c(AB)’ => cAB => cA & cB => c A’ & cB’ => cA’B’
" cA’ & cB’ => cA & cB => cAB => cAB)’
Отображение множеств:
f:Aна множестве А задано отображение f со значением множества B
aA; b=> b - образ элемента а при отображении f; a - прообраз элемента b при отображении f
Так как для каждого элемента из А ставится в соответствие элемент из В, значит А - область определения (Dom f=А), а область значенийB (Im f B)
Для отображения задают: 1) способ 2) Dom 3) Im
Отображение f инъективно если f(x)=f(x’) => x=x’(разные переходят в разные)
Отображение f сурьективно если Im f =B(каждый переходит в каждый)
Если же отображение инъективно+сурьективно, то множества равномощны(содержат одинаковое кол-во элементов), а отображение биективно - взаимооднозначно.
Счетные множества - множества равномощные множеству натуральных чисел (N)
Теорема: Множество Q счетно.
Докозательство: Q=![]()
Лемма 1: nN Z/n - счетно.
Каждому элементу из N надо взаимноднозначно сопоставить элемент Z/n:
10/n 5-2/n
2/n 63/n
3-1/n 7-3/n
42/n ...
Лемма 2: Объединение счетного или конечного(не более чем счетного) числа счетных множеств - счетно.
А1={а11, а12, а13,...}
А2={а21, а22, а23,...}
А3={а31, а32, а33,...}
...
Применяем диагональную нумерацию (а11 - 1; а21 - 2; а12 - 3; а31 - 4; а22 - 5...) и таким образом взаимнооднозначно сопоставляем каждому элементу из таблицы его номер, значит объединение счетного или конечного числа счетных множеств - счетно.
Часть может быть равномощна целому: (-1,1) равномощен R (через полуокружность и лучи)
Из Леммы1 и Леммы 2 получаем: Множество рациональных чисел счетно
2. Определение действительного числа бесконечной десятичной дробью. Плотность Q в R.
Действительные числа - множество чисел вида [a0],а1 a2 а3... где а0Z а1,а2,а3,...{0,1,...,9}
Действительное число представляется в виде суммы целой и дробной части:
[ао],а1 а2 а3...ак (0) = ао + а1/10 + а2/100 + ... +ак/10k = [ао],а1 а2 а3...а’к (9), где а’к=ак-1
х=[хо],х1 х2 х3...хк...
у=[уо],у1 у2 у3...ук...
х’к - катое приближение икса с недостатком = [хо],х1 х2 х3...хк
у”к - катое приближение игрека с избытком = [уо],у1 у2 у3...ук + 1/10k
х’к+1 > х’к (х’к - монотонно растет)
у”к+1 у”k (у”k - не возрастает), т.к. у”к=[уо],у1 у2 у3...ук + 1/10к
у”к+1 = [уо],у1 у2 у3...ук ук+1 + 1/10к+1
у”к - у”к+1 = 1/10к - ук+1 + 1/10к+1 0
10 - ук+1 - 1 / 10к+1 0
9 ук+1
Определение: 1) х > у к: х’к > у”к
2) х = у х’к не> у”к & у”к не> х’к
По определению получаем, что [1],(0)=[0],(9)
Свойства: 1)х, у либо ху, либо х=у
2) х>у & у>z => х>z
3) х не> х
Док-во (2): х>у у>z
х’к>у”к у’m>z”m
n=max{k;m}
х’nх’к>у”ку”n у’n у’m>z”mz”n
у”n>у’n => х’n>z”n
Определение: Если АR и х,уR аА: х у”к х х’к у”к у
х х’к / 2 + х’к / 2 > х’к / 2 + у”к / 2 > у”к / 2 + у”к / 2 > у
Видим: х > х’к / 2 + у”к / 2 > у, где (х’к / 2 + у”к / 2)Q
3.Несчетность множества действительных чисел.
Теорема: R несчетно.
Доказательство от противного:
1х1=[х1], х11 х12 х13... |
2х2=[х2], х21 х22 х23... | Пусть здесь нет девяток в периоде
3х3=[х3], х31 х32 х33... |
... | (*)
кхк=[хк ], хк1 хк2 хк3... |
... |
Найдем число которого нет в таблице:
с=[с], с1 с2 с3...
[с][х1] => сх1
с1 {9;х21} => сх2
с2 {9;х32} => сх3
...
ск {9;хк+1к} => схк
Таким образом С - число которое отсутствует в таблице (*)
5.Теорема Дедекинда о полноте R
Пусть 1) 0АR; 2) aA, b: а SupA=m => b: bm => B ограничено снизу => InfB=n, mn
Докажем, что m = n:
Пусть mс (с’n0 xNyNzN и Lim xN=x, Lim zN=z, причем x=z, то Lim yN=y => x=y=z.
Доказательство: n>n0 xNyNzN
Возьмем произвольно Е>0, тогда n’: n>n’ xN(х-Е,х+Е) & n”: n>n” zN(х-Е,х+Е) => n>max{n0,n’,n”} yN(x-E,x+E)
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
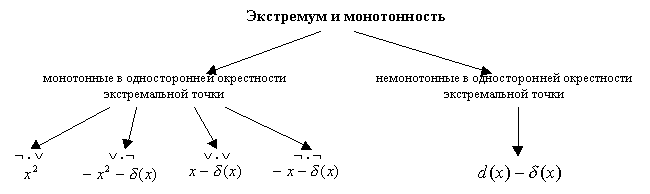
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
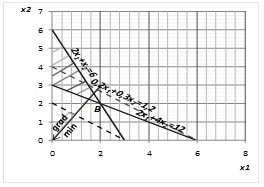
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





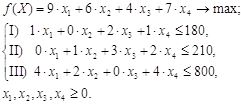
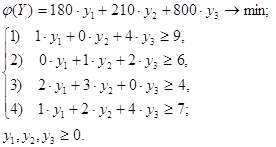
0 комментариев