Навигация
Определение предела последовательности и его единственность
5. Определение предела последовательности и его единственность.
Определение: Пусть даны два множества Х и У. Если каждому элементу хХ сопоставлен по определенному правилу некоторый элемент уУ, то говорят, что на множестве Х определена функция f и пишут f:ХУ или х (f(х)| хХ).
Определение: Последовательность-это ф-ция определенная на мн-ве N, со значениями во мн-ве R f:NR. Значение такой ф-ции в (.) nN обозначают аN.
Способы задания:
1) Аналитический: Формула общего члена
2) Рекуррентный: (возвратная) формула: Любой член последовательности начиная с некоторого выражаетс через предидущие. При этом способе задани обычно указывают первый член (или нсколько начальных членов) и формулу, позволющкю определить любой член последовательности через предидущие. Пример: а1=а; аN+1=аN + а
3) Словесный: задание последовательности описанием: Пример: аN = n-ый десятичный знак числа Пи
Определение: Число а называется пределом последовательности аN, если n0: n>n0 выполняется неравенство |аN-a| в ок рестности точки с содержится конечное число членов последовательности - противоречие с условием того, что с - предел последовательности.
Теорема: Сходящаяся последовательность ограничена.
Доказательство:
Пусть последовательность аN сходится к числу а. Возьмем какое-либо эпсилон, вне эпсилон-окрестности точки а лежит конечное число членов последо вательности, значит всегда можно раздвинуть окрестность так, чтобы все члены последовательности в нее попали, а это и означает что последователь ность ограничена.
Замечания: 1) Обратное не верно (аn=(-1)N, ограничена но не сходится)
2) Если существует предел последовательности аN, то при отбрасывании или добавлении конечного числа членов предел не меняется.
Порядковые свойства пределов:
Теорема о предельном переходе: Если Lim xN=x, Lim yN=y, n0: n>n0 хNyN, тогда xy
Доказательство(от противного):
Пусть х>у => по определению предела n0’: n>n0’ |хN-х|max{n0’, n0”} хN>yN - противоречие с условием.
Теорема: Если n0:n>n0 aNbNcN и Lim aN=a, Lim cN=c, причем a=c, то Lim bN=b => a=b=c.
Доказательство: Возьмем произвольно Е>0, тогда n’: n>n’ => cNn” => (a-E)max{n0,n’,n”} (a-E)bN(a-E,a+E)
9. Предел монотонной последовательности
Определение: Последовательность называется монотонно возрастающей (убывающей) если n1>n2 (n10 xE: (х-Е) n0 xNo>(х-E). Из монотон ности имеем: n>n0 xNxNo>(x-E), получили xNx=SupX, значит n>n0 xN(x-E,х] Lim(aN-bN)Lim(c’-c)Lim(bN-aN) => (a-b)Lim(c`-c)b-a) =>
0lim(c`-c)0 => 0(c`-c)0 => c’=c => c - единственное.
Перефразировка Леммы: Пусть имеется бесконечнаz посл-ть вложенных друг в друга промежутков (промежуток 1 вложен в промежуток 2 если все точки промежутка 1 принадлежат промежутку 2: [a1,b1],[a2,b2],...,[an,bn]..., так что каждый последующий содержится в предыдущем, причем длины этих промежутков стремятся к 0 при n lim(bN-aN)=0, тогда концы промежутков aN и bN стремятся к общему пределу с (с разных сторон).
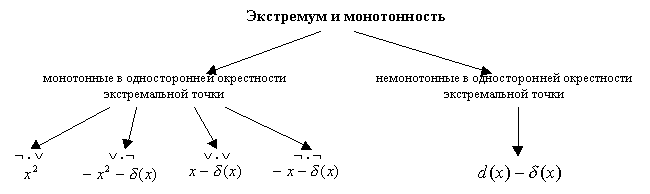
42.Локальный экстремум. Теорема Ферма и ее приложение к нахождению наибольших и наименьших значений.
Определение: Пусть задан промежуток I=(a;b), точка x0a;bТочка x0, называется точкой локалниого min(max), если для всех xa;bвыполняется
f(x0)f(x)).
Лемма: Пусть функция f(x) имеет конечную производную в точке x0. Если эта производная f‘(x0)>0(f‘(x0)f(x0) (f(x)0, то найдется такая окрестность (x0-,x0+) точки x0, в которой (при хx0) (f(x)-f(x0))/(x-x0)>0. Пусть x0 из предыдущего неравенства следует, что f(x)-f(x0)>0, т.е. f(x)>f(x0). Если же x-x теорема доказана.
Следствие: Если существует наибольшее (наименьшее) значение функции на [a;b] то оно достигается либо на концах промежутка, либо в точках, где производной нет, либо она равна нулю.
43.Теоремы Ролля, Лагранжа, Коши (о среднем значении).
Теорема Ролля
Пусть 1) f(x) определена и непрерывна в замкнутом промежутке [a;b]
2) сущестует конечная производная f’(x), по крайней мере в отткрытом промежутке (a;b)
3) на концах промежутка функция принимает равные значения: f(a)=f(b)
Тогда между a и b найдется такая точка c(am. По второй теореме Вейерштрасса оба эти значения функцией достигаются, но, так как f(a)=f(b), то хоть одно из них достигается в некоторой точ ке с между a и b. В таком случае из теоремы Ферма (Пусть функция f(x) определена в некотором промежутке I=(a;b) и во внутренней точке x0 этого промежутка принимает наибольшее (наименьшее) значение. Если функция f(x) дифференцируема в точке x0, то необходимо f‘(x0)=0) следует, что произ водная f’(с) в этой точке обращается в нуль.
Теорема Коши:
Пусть 1) f(x) и g(x) непрерывны в замкнутом промежутке [a;b] & g(b)g(a)
2) сущестуют конечные производные f’(x) и g’(x), по крайней мере в отткрытом промежутке (a;b)
3) g’(x)в отткрытом промежутке (a;b)
Тогда между a и b найдется такая точка c(an0 тогда при тех же значениях n будет верно |аKn-а| n: ахNb. Поделим промежуток [a,b] пополам, хотя бы в одной его половине содержится бесконечное множество членов посл-ти хN (в противном случае и во всем промежутке содержится конечное число членов посл-ти, что невозможно). Пусть [а1,b1] - та половиа, которая содержит бесконечное число членов посл-ти. Аналогично выделим на промежутке [а1,b1] промежуток [а2,b2] также содержащий бесконечное число членов посл-ти хN. Продолжая процесс до бесконечности на к-том шаге выделим промежуток [аK,bK]-также содержащий содержащий бесконеч ное число членов посл-ти хN. Длина к-того промежутка равна bK-аK = (b-a)/2K, кроме того она стремится к 0 при к и аKаK+1 & bKbK+1. Отсюда по лемме о вложенных промежутках ! с: n аNcbN.
Теперь построим подпоследовательность:
хN1 [а1,b1]
хN2 [а2,b2] n2>n1
. . .
хNK[аK,bK] nK>nK-1
ахNkb. (Lim aK=LimbK=c из леммы о вложенных промежутках)
Отсюда по лемме о зажатой последовательности Lim хNk=c - ч.т.д.
12.Верхний и нижний пределы последовательности.
xN - ограниченная последовательность =>n аNхNbN
хNKх, так как хNK-подпоследовательность => n ахNb =>ахb
х - частичный предел последовательности хN
Пусть М - множество всех частичных пределов.
Множество М ограничено (аМb) => SupM & InfM
Верхним пределом посл-ти xN называют SupMSup{xN}: пишут Lim xN
Нижним предел ом посл-ти xn называют InfMnf{xN}: пишут lim xN
Cуществование нижнего и верхнего пределов вытекает из определения.
Достижимость:
Теорема: Если хN ограничена сверху (снизу), то подпосл-ть хNK: предел которой равен верхнему (нижнему) пределу хN.
Доказательство: Пусть х=SupM=верхний предел хN
х’М: х-1/к подпоследовательность хNSх’ => Е>0 (в частности Е=1/к) s0: s>s0 =>
х’-1/к по доказанному для >0 получаем, Lim 1/(xN) = 1 => Lim (xN)
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
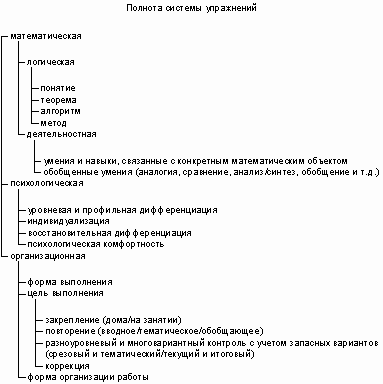
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
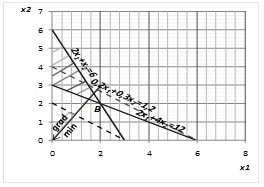
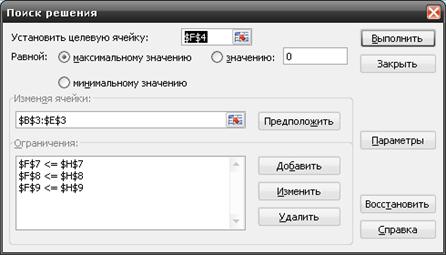
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





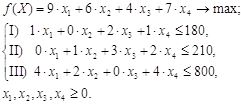
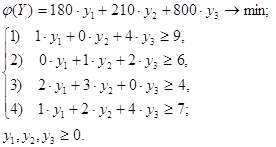
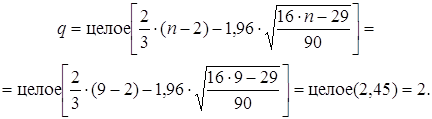
0 комментариев