Навигация
Верхние и нижние грани числовых множеств
4. Верхние и нижние грани числовых множеств.
Определение: АR mR, m - верхняя (нижняя) грань А, если аА аm (аm).
Определение: Множество A ограничено сверху (снизу), если существует такое m, что аА, выполняется аm (аm).
Определение: SupA=m, если 1) m - верхняя грань A
2) m’: m’ m’ не верхняя грань A
InfA = n, если 1) n - нижняя грань A
2) n’: n’>n => n’ не нижняя грань A
Определение: SupA=m называется число, такое что: 1) aA am
2) >0 aA, такое, что aa-
InfA = nназывается число, такое что: 1) 1) aA an
2) >0 aA, такое, что aEa+
Теорема: Любое, непустое ограниченное сверху множество АR, имееет точную верхнюю грань, причем единственную.
Доказательство:
Построим на числовой прямой число m и докажем что это точная верхняя грань А.
[m]=max{[a]:aA} [[m],[m]+1]A=>[m]+1 - верхняя грань A
Отрезок [[m],[m]+1] - разбиваем на 10 частей
m1=max[10*{a-[m]:aA}]
m2=max[100*{a-[m],m1:aA}]
...
mк=max[10K*{a-[m],m1...mK-1:aA}]
[[m],m1...mK, [m],m1...mK + 1/10K]A=>[m],m1...mK + 1/10K - верхняя грань A
Докажем, что m=[m],m1...mK - точная верхняя грань и что она единственная:
к: [m’K,m”K)Aк аА: аm”K => к: а’K>m”K => аа’K>m”K - это противоречит ограниченности => am
Точная верхняя грань:
Пусть ll”K, но так как к [m’K,m”K)A => а[m’K,m”K) => а>l =>l - не верхняя грань.
Теорема: Любое, непустое ограниченное снизу множество АR, имееет точную нижнюю грань, причем единственную.
Рассмотрим множество B{-а: аА}, оно ограничено сверху и не пусто => -SupB=InfA
6.Бесконечно малые и бесконечно большие последовательности. Их свойства.
Определение: Последовательность аN называется бесконечно малой (бм) если ее предел равен нулю (Е>0 n0: n>n0 |аN|n’: |aN|n”: |bN|max{n’,n”} выполнены оба неравен ства |aN| max{n’,n”} имеем: |cN|=|aN+bN||aN|+|bN| |dN|=|aN-bN| |aN|+|bN|n0 |aN|n0: |zN|=|aN*bN|=|aN|*|bN|n’ последовательностьть |bN|aN => bN - бм
Доказательство: aN - бм => n”: n>n”: |aN|=max{n’,n”} |bN||aN|0 n0: n>n0 |аN|>Е)
Теорема: Если aN - бм, то 1/aN - бб последовательностьть, обратное тоже верно.
Доказательство:
"=>" aN-бм=>вне любой эпсилон-окрестности точки 0 (в частности 1/Е) находится конечное число членов посл-ти, т.е. n0: n>n0 |aN|1/|aN|>Е.
" Е>0 n0: n>n0 1/|aN|>1/Е => |aN|n’ последовательность bN|aN| => bN - бб.
Доказательство: aN - бб => n”: n>n” |aN|>Е. Для n>max{n’,n”} bN|aN|>Е
7.Арифметика пределов
Предложение: Число а является пределом последовательности aN если разность aN-a является бм (обратное тоже верно)
Докозательство: Т.к. Lim aN=a, то |aN-a| (xN+yn)-(х+у)-бм, дальше по предложению)
2) xN*yN - х*у = х*N+у*N+N*N (По теоремам о сумме бм посл-тей и * бм посл-тей на огр. посл-ти получаем: xN*yN - х*у - бм, дальше по предл-нию)
3) xN/yN - х/у = (у*N-х*N) / (у*(у+N))= (у*N-х*N) * 1/у * 1/уN доказательство сводится к доказательству утверждения: если уn - сходящаяся не к 0 посл-ть, то 1/уN тоже сходящаяся последовательность: Lim уN=y => по определению предела получаем n0: n>n0 |уn-у|1/|уN| n: 1/|уN|max{2/у, 1/у1, 1/у2,...1/уno}
Теорема: Если хN сходится к х, yN сходится к у и n0: n>n0 последовательность хNуN, то ху
Доказательство(от противного): Пусть х>у. Из опр. предела E>0 (в частности Еn’ |xN-x|n” |yN-y|max{n’,n”} все члены посл-ти xN будут лежать в Е-окрестности точки х, а все члены посл-ти уN будут лежать в Е-окрестности точки у, причем
(х-Е,х+Е)(у-Е,у+Е)=. И т.к мы предположили, что х>у, то n>max{n’,n”}: хN>уN - противоречие с условием => ху.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
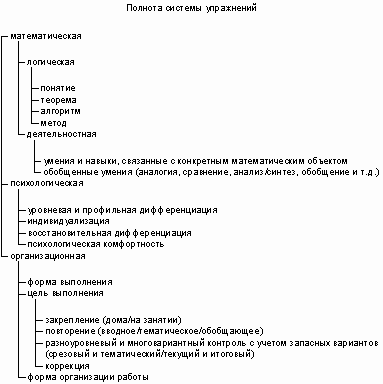
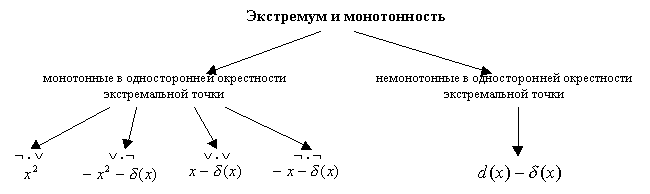
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
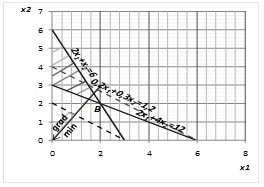
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





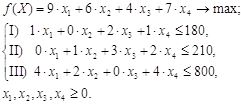
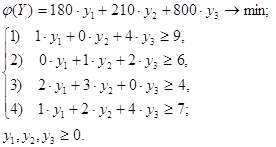
0 комментариев