Навигация
Доказательство формулы e=
15. Доказательство формулы e=...
yN=![]() ; zN=yN +
; zN=yN +![]()
1) yN монотонно растет
2) yNn0 00. Тогда Lim f(x) в точке х0 существует когда cуществуют правый и левый предел f(x) в точке х0 и они равны между собой.
Необходимость: Пусть предел f(х) существует и равен А => Е>0 >0: - f(х) попадает в интервал (f(х)-А,f(х)+А) => правый предел существует и он равен А. Если х попадает в интервал (x0-,0) => x попадает в интервал (x0-,x0+) => f(х) попадает в интер вал (f(х)-А,f(х)+А) => левый предел существует и он равен А.
Достаточность: Lim (х0|h|) при h0: Lim(х0+|h|) = Lim(х0-|h|)=А
Е>0 ’ >0: 00: -”1 при z>0, то aX aZ=(a1/N)M => a1/N>1 => (a1/N)M>1 => aX*(aZ-1)>1, (a>1 n>0)
5) при x0 aX1 (xR)
Т.к. Lim a1/N=1 (n), очевидно, что и Lim a-1/N=Lim1/a1/N=1 (n). Поэтому Е>0 n0: n>n0 1-E aX * aY = aX+Y
2) aX / aY = aX-Y
3) (aX)Y=aX*Y
xNx, yKy => (aXn)Yk = aXn*Yk => (n) (aX)Yk=aX*Yk =>(k) (aX)Y=aX*Y
4) x aX1) - монотонность.
x xN aXn < aX’n => (n) aXaX’- монотонна
x-x`>q>0 => aX-X’ aQ>1 => aX-X’1 => aX0 n0: n>n0 1-E0 k0: n>n0 0k0 => nK>n0 => 0 (1+1/zK+1)Zk+1/(1+1/zK+1) < (1+xK)1/Xk < (1+1/zK)Zk*(1+1/zK) kучитывая, что: (1+1/zK)1 (1+1/zK+1)1 => получаем:
eLim (1+xK)1/Xke => Lim (1+xK)1/Xk=e => Lim (1+x)1/X=e при x0+
Lim (1+xK)1/Xk при x0-:
yK=-xK0+ => доказываем аналогично предыдущему => получаем Lim (1+x)1/X=e при x0-
Видим что правый и левый пределы совпадают => Lim (1+x)1/X=e при x0
2) n lim (1+x/n)N = (lim (1+x/n)N/X)X = eX
3) xx R - непрерывна
x=(eLn x)=e*Ln x
непр непр непр непр
xLn x*Ln*Ln x => xe*Ln x
4) x0 Lim (Ln (1+x))/x = Lim Ln (1+x)1/X = Ln e = 1
4’) x0 Lim LogA(1+x)1/X = 1/Ln a
5) x0 Lim (eX-1)/x = {eX-1=t} = Lim t/Ln(1+t) => (4) = 1/1 = 1
5’) x0 Lim (aX-1)/x = Ln a
6) x0 Lim ((1+x)-1)/x = Lim ([e*Ln (1+x) -1/[Ln(1+x)]Ln (1+x)]/x = 11=
34.Теорема Вейрштрасса об ограниченности непрерывной функции на отрезке.
Функция хf(x) называется непрерывной на множестве Х если она непрерывна в каждой точке х этого множества.
Теорема: Функция непрерывная на отрезке [a,b], является ограниченной на этом отрезке (1 теорема Вейрштрасса) и имеет на нем наибольшее и наимень шее значение (2 теорема Вейрштрасса).
Доказательство: Пусть m=Sup{f(x):x[a,b]}. Если f не ограничена сверху на [a,b], то m=, иначе mR. Выберем произвольную возрастающую посл-ть (сN), такую что Lim cN=m. Т.к. nN: cN [a,b].
Для mR - по теореме о том, что предел произвольной подпосл-ти равен пределу посл-ти получаем cKnm.
Для m=+ - по Лемме о том что всякая подпосл-ть бб посл-ти явл-ся бб посл-тью получаем cKnm. Переходя к пределу в нер-вах cKn f()=m - что и означает что функция f ограничена сверху и достигает верхней
граница в точке . Существование точки =Inf{f(x):x[a,b]} доказывается аналогично.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
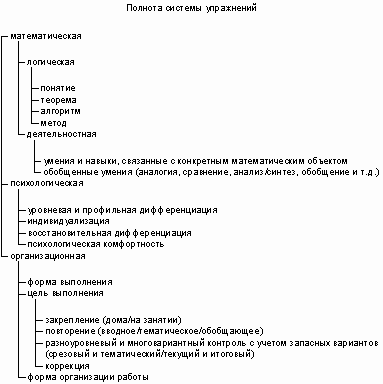
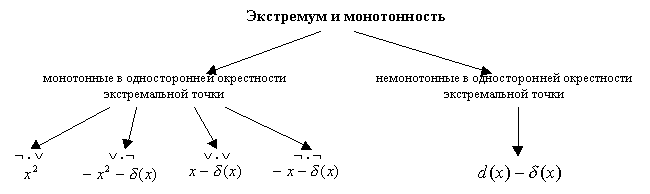
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
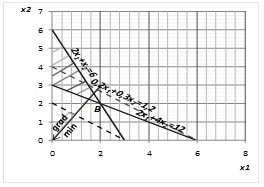
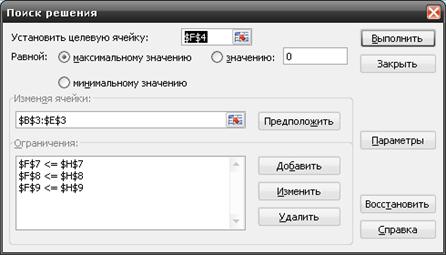
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





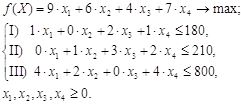
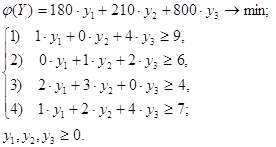
0 комментариев