Свойства функций от матриц

2. Свойства функций от матриц.

 

Свойство № 1. Если матрица имеет собственные значения  (среди них могут быть и кратные), а , то собственными значениями матрицы f(A) являются собственные значения многочлена f(x): .

Доказательство:

Пусть характеристический многочлен матрицы А имеет вид:

, , . Посчитаем . Перейдем от равенства к определителям:

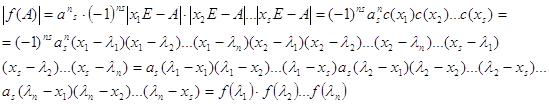
Сделаем замену в равенстве:

 (*)

Равенство (*) справедливо для любого множества f(x), поэтому заменим многочлен f(x) на , получим:

.

Слева мы получили характеристический многочлен для матрицы f(A), разложенный справа на линейные множители, откуда следует, что  – собственные значения матрицы f(A).

ЧТД.

Свойство № 2. Пусть матрица и  – собственные значения матрицы А, f(x) – произвольная функция, определенная на спектре матрицы А, тогда собственные значения матрицы f(A) равны .

Доказательство:

Т.к. функция f(x) определена на спектре матрицы А, то существует интерполяционный многочлен матрицы r(x) такой, что , а тогда f(A)=r(A), а у матрицы r(A) собственными значениями по свойству № 1 будут  которым соответственно равны .

ЧТД.

Свойство № 3. Если А и В подобные матрицы, , т.е. , и f(x) – произвольная функция, определенная на спектре матрицы А, тогда

Доказательство:

Т.к. А и В подобны, то их характеристические многочлены одинаковы Þ одинаковы и их собственные значения, поэтому значение f(x) на спектре матрицы А совпадает со значение функции f(x) на спектре матрицы В, при чем существует интерполяционный многочлен r(x) такой, что f(A)=r(A), ,  Þ .

ЧТД.

 

Свойство № 4. Если А – блочно-диагональная матрица , то

 

Следствие: Если , то , где f(x) – функция, определенная на спектре матрицы А.

4. Интерполяционный многочлен Лагранжа-Сильвестра.

Случай № 1.

Пусть дана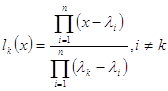 . Рассмотрим первый случай: характеристический многочлен  имеет ровно n корней, среди которых нет кратных, т.е. все собственные значения матрицы А различны, т.е. , Sp A – простой. В этом случае построим базисные многочлены l_k(x):

.

Пусть f(x) – функция, определенная на спектре матрицы А и значениями этой функции на спектре будут . Надо построить .

Построим:

.

Обратим внимание, что .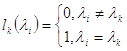

Пример: Построить интерполяционный многочлен Лагранжа-Сильвестра для матрицы .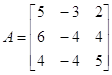

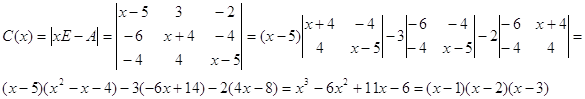Построим базисные многочлены:

Тогда для функции f(x), определенной на спектре матрицы А, мы получим:

.

Возьмем , тогда интерполяционный многочлен

.

 

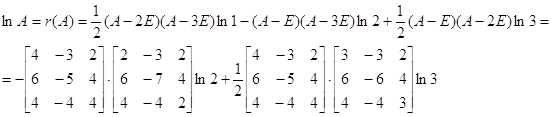Случай № 2.

Характеристический многочлен матрицы А имеет кратные корни, но минимальный многочлен этой матрицы является делителем характеристического многочлена и имеет только простые корни, т.е. . В этом случае интерполяционный многочлен строится так же как и в предыдущем случае.

Случай № 3.

Рассмотрим общий случай. Пусть минимальный многочлен имеет вид:

,

где m₁+m₂+…+m_s=m, deg r(x)<m.

Составим дробно-рациональную функцию:

 и разложим ее на простейшие дроби.

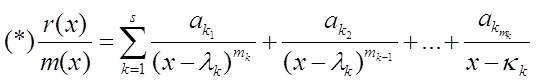
Обозначим: . Умножим (*) на  и получим

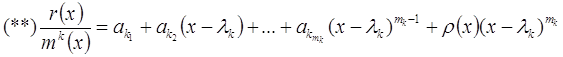
где – некоторая функция, не обращающаяся в бесконечность при .

Если в (**) положить , получим:

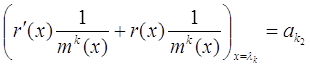
Для того, чтобы найти a_k3 надо (**) продифференцировать дважды и т.д. Таким образом, коэффициент a_ki определяется однозначно.

После нахождения всех коэффициентов вернемся к (*), умножим на m(x) и получим интерполяционный многочлен r(x), т.е.

.

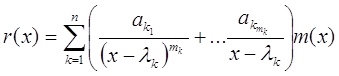Пример: Найти f(A), если , где t – некоторый параметр,

.

 

Найдем минимальный многочлен матрицы А:

.

Проверим, определена ли функция на спектре матрицы А

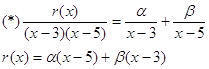
Умножим (*) на (х-3)

при х=3

Þ

Умножим (*) на (х-5)

.

Таким образом,  - интерполяционный многочлен.

 

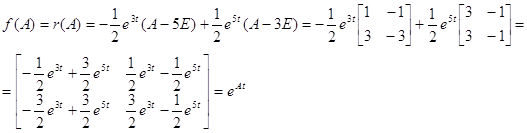
Пример 2.

Если 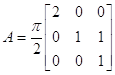, то доказать, что

Найдем минимальный многочлен матрицы А:

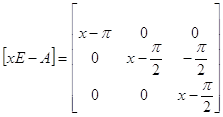- характеристический многочлен.

d₂(x)=1, тогда минимальный многочлен

.

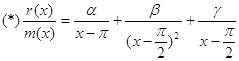Рассмотрим f(x)=sin x на спектре матрицы:

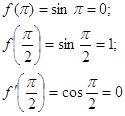Þ функция является определенной на спектре.

Умножим (*) на

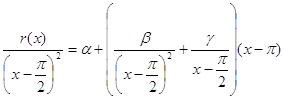Þ .

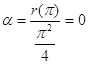Умножим (*) на :

.

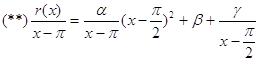
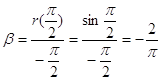Вычислим g, взяв производную (**):

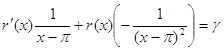. Полагая ,

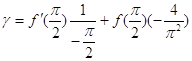, т.е. .

Итак, ,

,

,

.

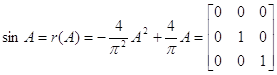ЧТД.

 

Пример 3.

Пусть f(x) определена на спектре матрицы, минимальный многочлен которой имеет вид . Найти интерполяционный многочлен r(x) для функции f(x).

Решение: По условию f(x) определена на спектре матрицы А Þ f(1), f’(1), f(2), f ‘(2), f ‘’ (2) определены.

.

 

.

Используем метод неопределенных коэффициентов:

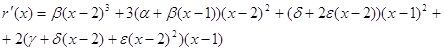
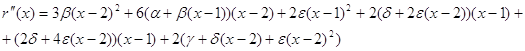
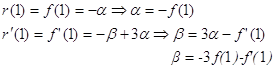
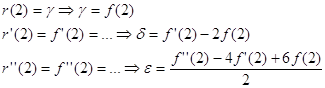
Если f(x)=ln x

f(1)=0 f’(1)=1

f(2)=ln 2 f’(2)=0.5 f’’(2)=-0.25