Навигация
1. f(x)=1
E=1Z11+0Z12+1Z21=Z11+Z21
2. f(x)=x-4
A-4E=0Z11+1Z12+(-2)Z21=Z12-2Z21
3. f(x)=(x-4)2
(A-4E)2=4Z21
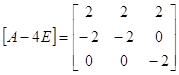
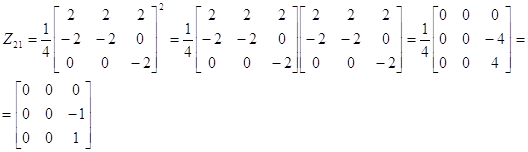
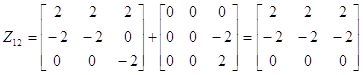
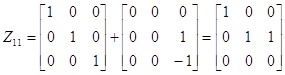 .
.
Таким образом, для любой функции f(x), определенное на спектре матрицы А
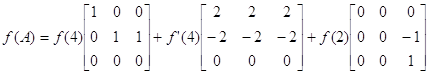
![]()
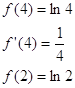
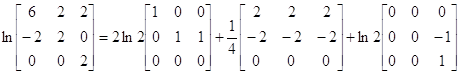
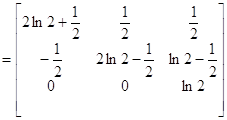 .
.
Пример 2.
Найти компоненты для матрицы
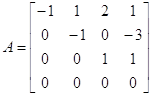 .
.
Найдем минимальный многочлен матрицы А.
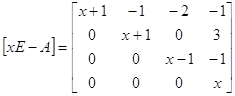
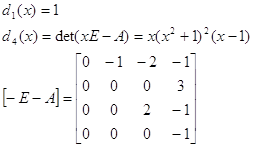
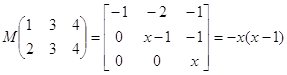
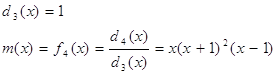
![]()
![]()
1. f(x)=1
E=Z11+Z21+Z31
2. f(x)=x+1
(A+E)=2Z21+Z31+Z12
3. f(x)=(x+1)2
(A+E)2=4Z21+Z31
4. f(x)=x-1
A-E=-2Z11+Z12-Z31
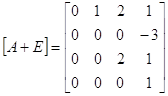
![]()
1. f(x)=1 E=Z11+Z21+Z31
2. f(x)=x+1 A+E=Z11Z22+2Z31
3. f(x)=(x+1)2 (A+E)2=Z11+4Z31
4. f(x)=x-1 (A-E)=-Z11-2Z21+Z22
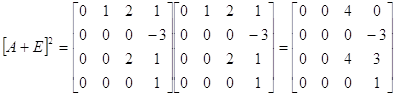
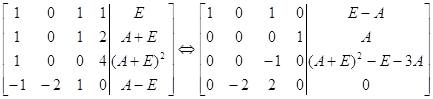
Z31=A
-Z22=(A+E)2-E-3A
Z12=Z22
Z11=(E-A)-Z22
6.Определенные матрицы.
Эрмитовы и квадратичные матрицы.
Пусть А – эрмитова матрица (А*=А).
Рассмотрим функцию h(x) – действительная функция комплексного аргумента.
Рассмотрим: ![]()
DF. Функция ![]() , где А – эрмитова матрица, называется эрмитовой формой от n переменных x1, …, xn, где А – матрица эрмитовой формы.
, где А – эрмитова матрица, называется эрмитовой формой от n переменных x1, …, xn, где А – матрица эрмитовой формы.
Очевидно, что если А – действительная симметрическая матрица, то в этом случае получаем квадратичную форму ![]() .
.
Для каждой эрмитовой (квадратичной) формы инвариантами являются: ранг (число не нулевых коэффициентов в квадратичной форме нормального вида совпадающих с рангом матрицы А), p (индекс) – число положительных коэффициентов в квадратичной форме нормального вида, оно совпадает с числом положительных собственных значений, сигнатура. Эти числа r, p, гр-r не зависят от тех преобразований, которые совершаются над данными формами.
В дальнейшем ограничимся рассмотрением только квадратичных форм. Нас интересуют 2 семейства матриц.
DF. Действительная симметрическая матрица А называется положительно определенной, если ![]() для
для ![]() .
.
DF. Действительная симметрическая матрица А называется неотрицательно определенной, если ![]() для
для ![]() .
.
Оба типа матриц относятся к классу определенных матриц. Заметим, что положительно определенная матрица невырожденная, т.е. если предположить, что она вырожденная, то ![]() ,
, ![]() , что противоречит условию.
, что противоречит условию.
Теорема № 1. Действительная симметрическая матрица n-го порядка будет определенной ранга ![]() тогда и только тогда , когда она имеет r положительных собственных значений, а остальные (n-r) – собственные значения равны 0.
тогда и только тогда , когда она имеет r положительных собственных значений, а остальные (n-r) – собственные значения равны 0.
Теорема № 2. Действительная симметрическая матрица положительна определена тогда и только тогда, когда все ее главные миноры положительны.
Теорема № 3. Действительная симметрическая матрица положительно определена тогда и только тогда, когда все ее главные миноры положительны.
7.Неотрицательные матрицы.
DF. Матрица ![]() называется неотрицательной, если каждый ее элемент положителен.
называется неотрицательной, если каждый ее элемент положителен.
Квадратные матрицы такого типа возникают во множестве задач и это определяющее свойство приводит к сильным результатам об их строении. Теорема Фробениуса-Перона является основным результатом для неотрицательных матриц.
Пусть матрицы ![]() . Будем говорить, что
. Будем говорить, что ![]() , если
, если ![]() б в частности A>B, если
б в частности A>B, если ![]() .
.
Вспомним матрицу перестановки ![]() , т.е. матрицы перестановки обязательно ортогональны. Произведение
, т.е. матрицы перестановки обязательно ортогональны. Произведение ![]() приводит
к перестановке столбцов матрицы А.
приводит
к перестановке столбцов матрицы А.
DF. При ![]() матрица
матрица ![]() называется приводимой матрицей, если существует такая матрица перестановки Р, что
называется приводимой матрицей, если существует такая матрица перестановки Р, что ![]() совподает с матрицей
совподает с матрицей 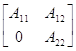 , где А11, А12, А22 – квадратные матрицы меньшего чем n порядка. Если матрица Р не существует, то матрица А называется неприводимой.
, где А11, А12, А22 – квадратные матрицы меньшего чем n порядка. Если матрица Р не существует, то матрица А называется неприводимой.
Понятие приводимости имеет значение при решении матричных уравнений ![]() , ибо если Ф – приводима, то осуществив замену переменных, которую подсказывают равенства
, ибо если Ф – приводима, то осуществив замену переменных, которую подсказывают равенства ![]() , получаем
, получаем
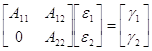 , где
, где 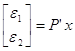 ,
, 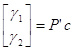 .
.
![]() и решаем матричное уравнение с матрицей более низкого порядка. Затем,
и решаем матричное уравнение с матрицей более низкого порядка. Затем, ![]() и решаем матричное уравнение. Таким образом, если А – приводима, то решение уравнения высокого порядка сводится к решению уравнений более низкого порядка, при чем собственные значения матриц А11 и А22 в своей совокупности составляет множество значений матрицы А.
и решаем матричное уравнение. Таким образом, если А – приводима, то решение уравнения высокого порядка сводится к решению уравнений более низкого порядка, при чем собственные значения матриц А11 и А22 в своей совокупности составляет множество значений матрицы А.
Интересно, что явление приводимости не связано с величиной матрицы, а зависит лишь от расположения нулевых элементов в матрице.
В связи с этим, используют идею направленного графа матрицы, которую можно взять в качестве характеризации неприводимости матрицы. Наметим первые шаги тоерии и получим вторую характеризацию неприводимости матриц.
DF. Пусть р1, р2, …, рn – n различных точек комплексной плоскости и ![]() . Для каждого нулевого элемента матрицы А
. Для каждого нулевого элемента матрицы А ![]() составим направленную линию от рi к рj
составим направленную линию от рi к рj![]() .
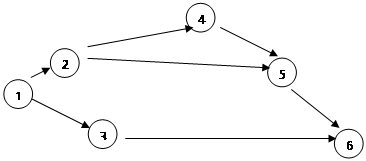
Получающаяся в результате фигура на комплексной плоскости называется направленным графом матрицы.
.
Получающаяся в результате фигура на комплексной плоскости называется направленным графом матрицы.
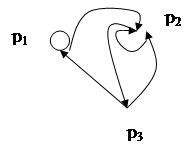
Например:
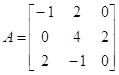
DF. Говорят, что любой направленный граф связен, если для каждой пары точек ![]() существует направленный путь
существует направленный путь ![]() .
.
Легко доказать, что квадратная матрица неприводима тогда и только тогда, когда ее граф является связным.
8.Теорема Фробениуса-Перона.
Очевидно, что если ![]() , то для
, то для ![]()
![]() . Более того, мы покажем, что для достаточно больших p
. Более того, мы покажем, что для достаточно больших p ![]() .
.
Лемма № 1. Если матрица ![]() неотрицательна и неприводима, то
неотрицательна и неприводима, то ![]() .
.
Доказательство:
Если взять произвольный вектор ![]() и
и ![]() , то
, то ![]() . И пусть вектор
. И пусть вектор ![]() имеет место, очевидно, что Z имеет по крайней мере столько же нулевых положительных элементов, что и y. В самом деле, если предположить, что Z имеет меньше нулевых компонент, то обозначим
имеет место, очевидно, что Z имеет по крайней мере столько же нулевых положительных элементов, что и y. В самом деле, если предположить, что Z имеет меньше нулевых компонент, то обозначим ![]() , тогда
, тогда ![]() и разбив матрицу А на блоки следующим образом
и разбив матрицу А на блоки следующим образом
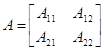 мы будем иметь
мы будем иметь 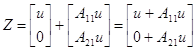 .
.
Учитывая, что ![]() , то
, то ![]() , тогда получаем, что
, тогда получаем, что ![]() , что противоречит неприводимости матрицы.
, что противоречит неприводимости матрицы.
Для следующего вектора повторим рассуждения и т.д. В итоге получим, что для некоторого ненулевого вектора y ![]() .
.
ЧТД.
Для ненулевой неприводимой матрицы А рассмотрим действительную функцию r(x), определенную для ненулевых векторов ![]() следующим образом:
следующим образом: ![]() , (Ax)i – i-я координата вектора Ах.
, (Ax)i – i-я координата вектора Ах.
![]() . Из определения следует, что
. Из определения следует, что ![]() и кроме того, r(x) –такое наименьшее значение
и кроме того, r(x) –такое наименьшее значение ![]() , что
, что ![]() .
.
Очевидно, что r(x) инвариантна относительна замены x на ![]() , поэтому в дальнейшем можно рассматривать замкнутое множество
, поэтому в дальнейшем можно рассматривать замкнутое множество ![]() , такое
, такое ![]() .
.
Однако, r(x) может иметь разрывы в точках, где координата x обращается в 0, поэтому рассмотрим множество векторов ![]() и обозначим
и обозначим ![]() . По лемме № 1 каждый вектор из N будет положительным, а поэтому
. По лемме № 1 каждый вектор из N будет положительным, а поэтому ![]() т.е.
т.е. ![]() для
для ![]() .
.
Обозначим через ![]() наибольшее число, для которого
наибольшее число, для которого ![]() ,
, ![]() .
. ![]() – спектральный радиус матрицы А. Если
– спектральный радиус матрицы А. Если ![]() Можно показать, что существует вектор y, что
Можно показать, что существует вектор y, что ![]() .
.
Замечание. Могут существовать и другие векторы в L для которых r(x) принимает значение r, поэтому любой такой вектор называется экстремальным для матрицы А (Az=rz).
Интерес к числу r объясняется следующим результатом.
Лемма № 2. Если матрица ![]() неотрицательна и неприводима, то число
неотрицательна и неприводима, то число ![]()
![]() является собственным значением матрицы А, кроме того каждый экстремальный вектор для А положителен и является правым собственным вектором для А, отвечающим собственному значению r.
является собственным значением матрицы А, кроме того каждый экстремальный вектор для А положителен и является правым собственным вектором для А, отвечающим собственному значению r.
Основным результатом является теорема Фробениуса-Перона для непрерывных матриц.
Теорема Фробениуса-Перона. Если матрица ![]() неотрицательна и неприводима, то:
неотрицательна и неприводима, то:
1. А имеет положительное собственное значение, равное спектральному радиусу матрицы А;
2. существует положительный правый собственный вектор, соответствующий собственному значению r.
3. собственное значение имеет алгебраическую кратность равную 1.
Эта теорема была опубликована в 1912 году Фробениусом и явилась обобщением теоремы Перона, которая является следствием.
Теорме Перона (следствие). Положительная квадратная матрица А имеет положительное и действительное собственное значение r, имеющее алгебраическую кратность 1 и превосходит модули всех других собственных значений матрицы А. Этому r соответствует положительный собственный вектор.
Используя теорему Фробениуса-Перона, можно найти максимальное действительное значение матрицы, не используя характеристического многочлена матрицы.
Похожие работы
... Тройка является решением игры <=>, когда является решением игры , где а – любое вещественное число, к>0 ГЛАВА 2. Игры с нулевой суммой в чистых стратегиях 2.1 Вычисление оптимальных стратегий на примере решения задач Используя теорему о минимаксе, можно утверждать, что каждая антагонистическая игра имеет оптимальные стратегии. Теорема: пусть А – матричная игра и строки данной ...
... -картину, не соответствующие ей, являются кандидатами на исключение из сферы деятельности корпорации. 5. Разработка корпоративной стратегии Предшествующий анализ подготовил почву для разработки стратегических шагов по улучшению деятельности диверсифицированной компании. Основное заключение о том, что делать, зависит от выводов, касающихся всего набора видов деятельности в хозяйственном ...
... систему сканирования, как средняя или даже крупная. Однако ряд других исследователей доказали наличие позитивной корреляционной взаимосвязи между размером фирмы и характером анализа макроокружения предприятия. Для эффективности деятельности организации чрезвычайно важно стратегическое видение ее руководителя, сложившееся на основе проведенного анализа макроокружения предприятия. С точки зрения, ...
... тенденции изменения показателя может быть единственным возможным способом прогнозирования (рис. 2.1) [4, c.35]. Рис. 2.1. Пример экстраполяции показателя 3. МЕТОДЫ ОПТИМИЗАЦИИ В ЭКОНОМИЧЕСКОМ АНАЛИЗЕ Основа всех приемов оптимизации – нахождение экстремума функции при заданных ограничениях. Например, нахождение максимума прибыли при ...
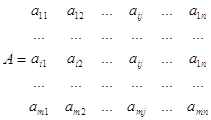
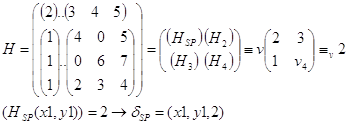
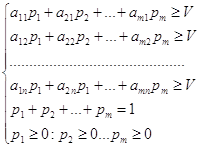
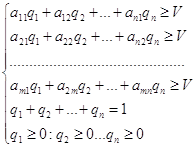




0 комментариев