Магнитогорский Государственный Технический Университет имени Г.И.Носова
Кафедра математики
Реферат
Тема: Метод прогонки решения систем с трехдиагональными
матрицами коэффициентов
Выполнил: студент группы ЭА-04-2
Романенко Н.А.
Проверил: Королева В.В.
Магнитогорск 2004
Часто возникает необходимость в решении линейных алгебраических систем, матрицы которых, являясь слабо заполненными, т.е. содержащими немного ненулевых элементов, имеют определённую структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов метод Гаусса можно трансформировать в более эффективные методы.
Рассмотрим наиболее простой случай ленточных систем, к которым, как увидим впоследствии, сводится решение задач сплайн-интерполяции функций, дискретизации краевых задач для дифференциальных уравнений методами конечных разностей, конечных элементов и др. А именно, будем искать решение такой системы, каждое уравнение которой связывает три “соседних” неизвестных:
bixi-1+cixi+dixi=ri (1)
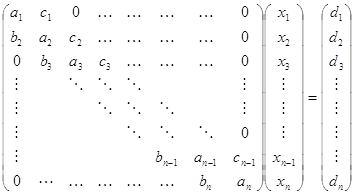
где i=1,2,...,n; b1=0, dn=0. Такие уравнения называются трехточечными разностными уравнениями второго порядка. Система (1) имеет трёхдиагональную структуру, что хорошо видно из следующего, эквивалентного (1), векторно-матричного представления:
![]()
![]()
![]()
![]()
![]()
![]() c1 d1 0 0 ... 0 0 0 x1 r1
c1 d1 0 0 ... 0 0 0 x1 r1
b2 c2 d2 0 ... 0 0 0 x2 r2
0 b3 c3 d3 ... 0 0 0 x3 r3
. . . . ... . . . * ... = ...
0 0 0 0 ... bn-1cn-1 dn-1 xn-1 rn-1
0 0 0 0 ... 0 bn cnxn rn
Как и в решении СЛАУ методом Гаусса, цель избавится от ненулевых элементов в поддиаганальной части матрицы системы, предположим, что существуют такие наборы чисел δi и λi (i=1,2,...,n), при которых
xi= δixi+1+ λi (2)
т.е. трехточечное уравнение второго порядка (1) преобразуется в двухточечное уравнение первого порядка (2). Уменьшим в связи (2) индекс на единицу и полученое выражение xi-1= δi-1xi+ λi-1 подставим в данное уравнение (1):
biδi-1 xi+ bi λi-1+ cixi+ dixi+1= ri
откуда
xi= -((di /( ci+ biδi-1)) xi-1+(ri - bi λi-1)/( ci - bi δi-1)).
Последнее равенство имеет вид (2) и будет точно с ним совпадать, иначе говоря, представление (2) будет иметь место, если при всех i=1,2,…,n выполняются рекуррентные соотношения
δi = - di /( ci+ biδi-1) , λ i=(ri - bi λi-1)/( ci - bi δi-1) (3)
Легко видеть, что, в силу условия b1=0, процесс вычисления δi, λi может быть начат со значений
δ1 = - d1/ c1 , λ1 = r1/ c1
и продолжен далее по формулам (3) последовательно при i=2,3,...,n, причем при i=n, в силу dn=0, получим δn=0.Следовательно, полагая в (2) i=n,будем иметь
xn = λn = (rn – bn λn-1)/( cn – bn δn-1)
(где λn-1 , δn-1 – уже известные с предыдущего шага числа). Далее по формулам (2) последовательно находятся xn-1 , xn-2 ,…, x1 при i=n-1, n-2,...,1 соответственно.
Таким образом, решение уравнений вида (1) описываем способом, называемым методом прогонки, сводится к вычислениям по трём простым формулам: нахождение так называемых прогоночных коэффициентов δi, λiпо формулам (3) при i=1,2,…,n (прямая прогонка) и затем неизвестных xi по формуле (2) при i=n-1, n-2,...,1 (обратная прогонка).
Для успешного применения метода прогонки нужно, чтобы в процессе вычислений не возникало ситуаций с делением на нуль, а при больших размерностях систем не должно быть строгого роста погрешностей округлений.
Будем называть прогонку корректной, если знаменатели прогоночных коэффициентов (3) не обращаются в нуль, и устойчивой, если |δi|<1 при всех i?{1,2,...,n }.
Приведем простые достаточные условия корректности и устойчивости прогонки, которые во многих приложениях метода автоматически выполняются.
Теорема
Пусть коэффициенты biи di уравнения (1) при i=2,3,...,n-1 отличны от нуля и пусть
|ci|>|bi|+|di| i=1,2,…,n. (4)
Тогда прогонка (3), (2) корректна и устойчива (т.е. сi+biδi-1≠0, |δi|<1).
Д о к а з а т е л ь с т в о. Воспользуемся методом математической индукции для установления обоих нужных неравенств одновременно.
При i=1, в силу (4), имеем:
|c1|>|d1|≥0
- неравенство нулю первой пары прогоночных коэффициентов, а так же
|δ1|=|- d1/ c1|<1
Предположим, что знаменатель (i-1)-x прогоночных коэффициентов не равен нулю и что |δi-1|<1. Тогда, используя свойства модулей, условия теоремы и индукционные предположения, получаем:
|сi+biδi-1|≥|ci| - |biδi-1|>|bi|+|di| - |bi|*|δi-1|= |di|+|bi|(1 - | δi-1|)> |di|>0
а с учетом этого
|δi|=|- di/ сi+biδi-1|=|δi|/| сi+biδi-1|<|δi|/|δi|=1
Следовательно, сi+biδi-1 ≠0 и |δi|<1 при всех i?{1,2,...,n }, т.е. имеет место утверждаемая в данных условиях корректность и устойчивость прогонки. Теорема доказана.
Пусть А – матрица коэффициентов данной системы (1), удовлетворяющих условиям теоремы, и пусть
δ1= - d1/ c1 , δi=|- di/ ci+biδi-1 (i=2,3,...,n-1), δn=0
- прогоночные коэффициенты, определяемые первой из формул (3), а
∆i= сi+biδi-1 (i=2,3,...,n)
- знаменатели этих коэффициентов (отличные от нуля согласно утверждению теоремы). Непосредственной проверкой легко убедится, что имеет место представление A=LU, где
![]()
![]() c1 0 0 0 ... 0 0 0
c1 0 0 0 ... 0 0 0
b2 ∆2 0 0 ... 0 0 0
L= 0 b3 ∆3 0 ... 0 0 0
…………………………
0 0 0 0 ... bn-1 ∆n-1 0
0 0 0 0 ... 0 bn ∆n
1 -δ1 0 0 ... 0 0 0
0 1 δ2 0 ... 0 0 0
U= 0 0 1δ3 ... 0 0 0
…………………………
0 0 0 0 ... 0 1 -δn-1
0 0 0 0 ... 0 0 1
Единственное в силу утверждение теоремы LU-разложения матриц. Как видим, LU-разложение трехдиагональной матрицы А может быть выполнено очень простым алгоритмом, вычисляющем ∆i δi при возрастающих значениях i. При необходимости попутно может быть вычислен
n
det A = c1 ∏ ∆i .
i=2
В заключение этого пункта заметим, что, во-первых, имеются более слабые условия корректности и устойчивости прогонки, чем требуется в теореме условие строгого диагонального преобладания в матрице А. Во-вторых, применяется ряд других, отличных от рассмотрения нами правой прогонки, методов подобного типа, решающих как поставленную здесь задачу (1) для систем с трехдиагональными матрицами (левая прогонка, встречная прогонка, немонотонная, циклическая, ортогональная прогонки и т.д.), так и для более сложных систем с матрицами ленточной структуры или блочно-матричной структуры (например, матричная прогонка).
Список используемой литературы
В.М. Вержбитский «Численные методы. Линейная алгебра и нелинейные уравнения», Москава «Высшая школа 2000».
Похожие работы
... уравнений (2) сводится к последовательному решению двух следующих систем уравнений с треугольными матрицами коэффициентов L Y = B; (6) U X = Y (7) линейный алгебраический уравнение численный где Y = - вектор вспомогательных переменных. Такой подход позволяет многократно решать системы линейных ...
... (19) где - матрица системы, - матрица правых частей, оценивается нормой: (20) Относительная погрешность оценивается по формуле: (21) где . 4. Итерационные методы решения систем линейных уравнений Рассмотрим систему линейных уравнений, которая плохо решается методами Гаусса. Перепишем систему уравнений в виде: ...
... лежащие на главной и двух побочных диагоналях, равны нулю при та В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных. Т.е. матрицу А можно записать Идея метода прогонки состоит ...
... неизвестных и матрица этой системы является трехдиагональной. Преобразуем уравнения (2.28): . (2.30) Введя обозначения получим , (i=0, 1,..., n-2). (2.31) Краевые условия по-прежнему запишем в виде . (2.32) Метод прогонки состоит в следующем. Разрешим уравнение (2.31) относительно : . (2.33) Предположим, что с помощью полной системы (2.31) из уравнения исключен член ...

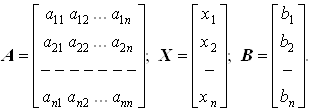



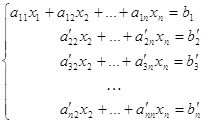
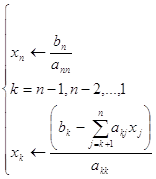
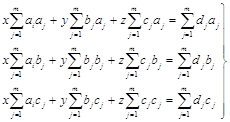
0 комментариев