Навигация
Методика обучения по курсу математики за 3 года
Работая над методической темой школы в течение трёх лет, МО учителей математики ставило перед собой следующие цели:
1. Строить учебный процесс с учетом индивидуальности каждого ребёнка: его потребностей, мотивов, активности, интеллекта.
2. научиться сотрудничать с учениками и научить сотрудничать между собой.
3. Добиваться взаимосвязи обучения и учения, обеспечивающей развитие личности как индивидуальности.
В процессе работы над темой решались следующие задачи:
- изучение индивидуальных особенностей каждого ребенка;
- определение формы дифференциации;
- воздействие на формирование творческого и интеллектуального потенциала каждого ребенка. Для достижения поставленных целей учителями МО был составлен план работы, в основу которого входило:
1. Изучение необходимой документации по личностно – ориентировочному подходу к процессу обучения и воспитания школьников.
2. Изучение индивидуальных особенностей каждого ребенка.
3. Обмен опытом работы по данной теме.
4. Уроки с личностно – ориентировочной направленностью.
5. Выступление на различных заседаниях по этой теме. Корректировка плана самообразования учителей с учетом методической темы школы. Приступая к работе по данной теме учителями МО были изучены следующие материалы:
1) И.С Якиманская «Личностно – ориентировочное обучение в современной школе», М , 1996г.
2) Р.Г. Карандашова методическая разработка «Дифференциация в образовании как средства реализации личностно – ориентировочного подхода к учащимся», Ставрополь, СКИППРО, 1999г.
3) «Культура современного урока» под редакцией Н.Е. Щурковой, М , 1998г.
4) И.М. Чередов «Формы учебной работы в средней школе», М, 1998г.
На заседаниях МО заслушивались и обсуждались следующие вопросы по данной теме;
«Развитие математических способностей как средство развития личности школьника» (Попова В.И.); «Дифференциация самостоятельных работ школьников» (Байш Н.П.); «Личностно – ориентировочный подход в обучении математики» (Позднякова И.В.); «Индивидуальная работа с учащимися как средство повышения интереса к предмету» (Семыкина С.В.); «Активизация познавательной деятельности на уроках математики» (Кузнецова О.Н.); « Развитие интереса на уроках математики» (Малышева Н.В.), «Моделирование урока математики» (Звягинцева Т.Б.).
Работая над темой учителя МО, используют следующие принципы педтехники:
- принцип свободы выбора;
- принцип открытости;
- принцип деятельности;
- принцип обратной связи;
- принцип идеальности;
Приступая к работе над темой школы «Личностно – ориентировочный подход к процессу обучения и воспитания учащихся», Кузнецова О.Н. изучила следующую литературу:
=2=
1. Дерзкие формулы творчества: сборник (составитель Селюцкий А.Б. – Петрозаводск: Карелия, 1987г.).
2. Правила игры без правил: сборник (составитель Селюцкий А.Б.,1989г.)
3. Злошин Б.Л., Зусман А.В. изобретатель пришел на урок,1989г.
4. Альтшулер Г.С. Найти идею, 1996г.
Для успешной работы Ольга Николаевна проводит тестирование учащихся в начале каждого учебного года. В тестирование она включает вопросы по определению базы математических знаний учащихся; определению типа внимания. По результатам этих тестов Ольга Николаевна планирует индивидуальную работу с каждым учащимся. В своём планировании она учитывает также результаты входных срезов.
На своих уроках, ориентированных на личность, использует следующие приёмы и методы:
- Опрос у доски. Но только, если уверена, что ответ этот будет блестящим, чтобы он выглядел как образец ответа, к которому нужно стремиться всем остальным.
- Опрос по цепочке. Его Ольга Николаевна использует чаще, чем предыдущий, но старается, чтобы получился логический, связанный, развернутый рассказ.
- Тихий опрос. Беседа проводится полушепотом с одним или несколькими учащимися, в то время как другие заняты работой.
- Работа в группах. Часто применятся при повторении и обобщении. Одним группам даются задания теоретические (составить конспект по определенной теме), а другим практические. Создаются также группы для выполнения творческих заданий.
- Взаимный опрос.
Развитию познавательной активности учащихся способствуют недели математики, которые ежегодно проводятся в нашей школе. В 1999-2000 учебном году Кузнецова А.В. в 7А классе проводила «парад геометрических фигур», который прошел в форме театрализованного представления, с вкраплением занимательных задач. Дети разбились самостоятельно на 3 команды (учитывалась психологическая совместимость учащихся):
1. Прямая и её родственники.
2. Углы.
3. Треугольники.
Каждая команда подготовила костюмы, сочинила песню о своей фигуре, частушки об одноклассниках и т.п.
Также мероприятия позволяют каждому школьнику проявить свои не только интеллектуальные, но и артистические способности; поверить в свои силы, способствуют повышению интереса к учебной деятельности; формируют положительные мотивы учения.
Основная цель современной школы – создать такую систему образования, - которая бы обеспечивала образовательные потребности личности в соответствии с её склонностями, интересами и возможностями, создавала бы условия для самореализации, готовила бы к творческому интеллектуальному труду.
Знания в области математики являются необходимой составной частью интеллектуального баланса каждого образованного человека.
Универсальный элемент мышления – логика. Искусство определять и умение работать с определениями; умение отличать известное от неизвестного, доказанное от недоказанного, искусство анализировать, классифицировать, ставить гипотезы,
=3=
пользоваться аналогиями – всё это и многое другое человек осваивает в значительной мере именно благодаря изучению математики.
В своей работе при изучении математики с учащимися Попова В.И. ставит следующие цели:
- интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для полноценной жизни в обществе;
- овладение конкретными математическими знаниями, умениями и навыками, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
- воспитание личности в процессе освоения математики и математической деятельности.
Хорошее значение возрастных психологических особенностей учащихся при широком использовании педагогики сотрудничества позволяет Валентине Ивановне осуществить личностный подход в воспитании и обучении.
Во-первых, она практикует планирование системы уроков по теме, в конце которой проводит зачёт.
При изучении темы, учитель анализирует количество часов, теоретический материал и практические задания; решает все задачи, предлагаемые в учебнике для того, чтобы выделить ключевые, к которым сводятся все остальные; выделяет, какие задачи нужны для коллективного решения, какие – для группового, какие – для индивидуального, для самостоятельной работы и домашнего задания.
Такие уроки организуют активную работу класса в целом и каждого ученика в отдельности, заставляют детей задумываться о своих способностях и возможностях, появляется желание мыслить и развивать свою память, смекалку.
Большое значение Валентина Ивановна придает усилению прикладной направленности математики. Для реализации поставленных задач каждая тема определена идеей.
Например, в 8 классах
Тема: Функция.
Идея: Моя функция в мире. Я функциональная единица великого целого – мироздания.
Похожие работы
... вероятностей совместимых событий; формулы: полной вероятности, Бейеса (Байеса). Одной из форм дифференцированного обучения по курсу теории вероятностей может являться факультативный курс. 2. Разработка программы факультативного курса по теории вероятностей в курсе математики 8 класса 2.1 Основные понятия о факультативном курсе Возможность 1-2 часа в неделю дополнительно работать со ...
... (вопросы а) и в)). Понятие функции, в системе формирования которого должны присутствовать такие задания, сразу выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения. Методика введения понятий: функции, аргумента, области определения. Не смотря на чрезвычайно большой объем, широту и сложность понятия функции, его ...
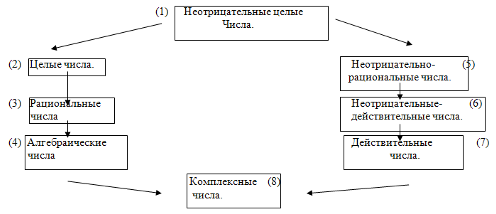
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
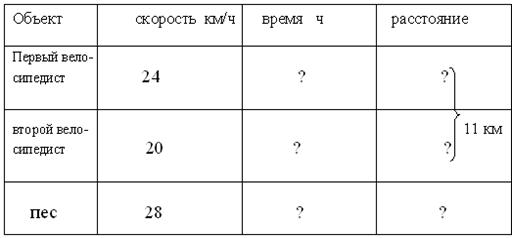
... способом аналитико – синтетический метод применяется на тех – же решениях. Единственное различие состоит в том , что на этапе поиска решения применяется анализ в нисходящей форме. Методика обучения решения технических задач. Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими, арифметическими и т.д) ...
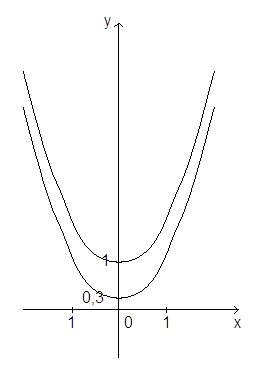
0 комментариев