Форма кусочно-постоянного (мозаичного) цветного изображения

4. Форма кусочно-постоянного (мозаичного) цветного изображения.

Во многих практически важных задачах форма объекта на изображении может быть охарактеризована специальной структурой излучения, достигающего поле зрения X в виде здесь  - индикаторные функции непересекающихся подмножеств А_i, i=1,…...,N, положительной меры поля зрения Х, на каждом из которых функции 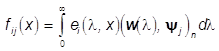, , j=1,...,n, i=1,...,N, непрерывны. Поскольку согласно лемме 2

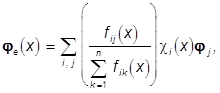
  , (3)

то цветное изображение f_e(×), такого объекта характеризует его форму непрерывным распределением яркости и цвета на каждом подмножестве A_i, i=1,...,N. Для изображения ,  где , также характерно напрерывное распределение яркости и цвета на каждом A_i, если , - непрерывные функции.

Если, в частности, цвет и яркость  постоянны на A_i, i=1,...,N, то это верно и для всякого изображения , если  не зависит явно от . Для такого изображения примем следующее представление:

, (4)

его черно-белый вариант

  (4*)

на каждом A_i имеет постоянную яркость , и цвет изображения 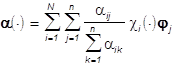(4)

  (4**)

не меняется на A_i и равен 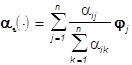, i=1,...,N.

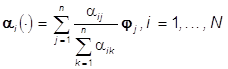Поскольку для реальных изображений должно быть выполнено условие физичности (2*), , то форму изображения (4), имеющего на различных множествах А_i имеет несовпадающие яркости  и различные цвета , определим как выпуклый замкнутый в конус:

 . (4***)

v(a), очевидно, содержится в n×N мерном линейном подпространстве

 , (4****)

 которое назовем формой a(×) в широком смысле.

Форму в широком смысле любого изображения a(×), у которого не обязательно различны яркости и цвета на различных подмножествах A_i ,i=1,...,N, определим как линейное подпространство , натянутое не вектор-функции Fa(×),FÎF, где F - класс преобразований , определенных как преобразования векторов a(x)®Fa(x) во всех точках xÎX; здесь F - любое преобразование . Тот факт, что F означает как преобразование , так и преобразование , не должен вызывать недоразумения.

Изображения из конуса(4***) имеют форму, которая не сложнее, чем форма a(×) (4), поскольку некоторые из них могут иметь одно и то же значение яркости или(и) цвета на различных множествах А_i, i=1,…………..,N. Также множества оказываются, по существу, объединенными в одно, что и приводит к упрощению формы изображения, поскольку оно отражает меньше деталей формы изображенного объекта, чем изображение (4). Это замечание касается и L(a(×)), если речь идет о форме в широком смысле.

Лемма 3. Пусть {А_i} - измеримое разбиение X: .

Изображение (3) имеет на каждом подмножестве A_i :

- постоянную яркость  и цвет  , если и только если выполняется равенство (4);

- постоянный цвет , если и только если в (3) ;

- постоянную яркость f_i , i=1,...,N, если и только если в (3)  не зависит от , i=1,…...,N.

Доказательство . На множестве A_i яркость и цвет изображения (3) равны соответственно[6]

 , , i=1,.…..,N.

Если выполнено равенство (4), то и  от  не зависят. Наоборот, если  и , то и , т.е. выполняется (4).

Если , то цвет  не зависит от  . Наоборот, пусть  не зависит от . В силу линейной независимости  координаты j_(i)(x) не зависят от  , т.е.  и, следовательно, где  - яркость на A _i и . Последнее утверждение очевидно n

Цвет изображения определяется как электродинамическими свойствами поверхности изображенного объекта, так и спектральным составом облучающего электромагнитного излучения в том диапазоне, который используется для регистрации изображения. Речь идет о спектральном составе излучения, покидающего поверхность объекта и содержащего как рассеянное так и собственное излучения объекта. Поскольку спектральный состав падающего излучения, как правило, пространственно однороден, можно считать, что цвет изображения несет информацию о свойствах поверхности объекта, о ее форме, а яркость в значительной степени зависит и от условий “освещения”. Поэтому на практике в задачах морфологического анализа цветных изображений сцен важное значение имеет понятие формы изображения, имеющего постоянный цвет и произвольное распределение яркости в пределах заданных подмножеств A_i , i=1,...,N, поля зрения X.

Итак, пусть в согласии с леммой 3

 , (5)

где,  - индикаторная функция A_i, , функция g_i(×) задает распределение яркости

(6)

в пределах A_i при постоянном цвете

, i=1,...,N, (7)

причем для изображения (5) цвета j_(i), i=1,.…..,N, считаются попарно различными, а функции g_(i), i=1,.…..,N, - удовлетворяющими условиям  i=1,.…..,N.

Нетрудно заметить, что в выражениях (5),(6) и (7) без потери общности можно принять условие нормировки , позволяющее упростить выражения (6) и (7) для распределений яркости и цвета. С учетом нормировки распределение яркости на A_i задается функцией  а цвет на A_i равен

(7*)

Форму изображения (5) определим как класс всех изображений

(8)

,

каждое из которых, как и изображение (5), имеет постоянный цвет в пределах каждого A_i, i=1,...,N. Форма таких изображений не сложнее, чем форма f(×) (5), поскольку в изображении  на некоторых различных подмножествах A_i, i=1,...,N, могут совпадать значения цвета, которые непременрно различны в изображении f(×) (5). Совпадение цвета  на различных подмножествах A_i, i=1,...,N ведет к упрощению формы изображения  по сравнению с формой f(×) (5). Все изображения , имеющие различный цвет на различных A_i, i=1,...,N, считаются изоморфными f(×) (и между собой), форма остальных не сложнее, чем форма f(×). Если , то, очевидно, .

Если в (8) яркость , то цвет  на A_i считается произвольным (постоянным), если же  в точках некоторого подмножества , то цвет  на A_i считается равным цвету  на , i=1,...,N.

Цвет изображения (8) может не совпадать с цветом (5). Если же по условию задачи все изображения , форма которых не сложнее, чем форма , должны иметь на A_i, i=1,...,N, тот же цвет, что и у  то следует потребовать, чтобы , в то время, как яркости  остаются произвольными (если , то цвет  на A_i определяется равным цвету f(×) на A_i, i=1,...,N).

Нетрудно определить форму любого, не обязательно мозаичного, изображения f(×) в том случае, когда допустимы произвольные изменения яркости  при неизменном цвете j(x) в каждой точке . Множество, содержащее все такие изображения

(9)

назовем формой в широком смысле изображения , у которого f(x)¹0, m-почти для всех , [ср. 2].  является линейным подпространством , содержащем любую форму

, (10)

в которой включение определяет допустимые значения яркости. В частности, если означает, что яркость неотрицательна: , то  - выпуклый замкнутый конус в , принадлежащий .

Более удобное описание формы изображения может быть получено на основе методов аппроксимации цветных изображений, в которых форма определяется как оператор наилучшего приближения. В следующем параграфе дано представление формы изображения в виде оператора наилучшего приближения.

Похожие работы

Применение материалов Аэрофотосъемки при инвентаризации лесов

Скачать

31041

0

2

... непосредственно в лесу, анализируя полученные в натуре таксационные характеристики и сопостав­ляя их с изображением всей площади таксационного выдела на аэрофотоснимках. ИНВЕНТАРИЗАЦИЯ ЛЕСОВ НА ОСНОВЕ СОЧЕТАНИЯ НАЗЕМНОЙ ТАКСАЦИИ С КАМЕРАЛЬНЫМ ДЕШИФРИРОВАНИЕМ АЭРОФОТОСНИМКОВ Метод предусматривает частичную замену наземной такса­ции камеральным дешифрированием ...

Ландшафтно-экологические методы исследований

Скачать

258002

3

0

... приходит, с карты начинается и картой кончается». «Карта... способствует выявлению географических закономерностей». «Карта является как бы вторым языком географии...». По К.А. Салищеву, картографический метод исследования заключается в использовании разнообразных карт для описания, анализа и познания явлений, для получения новых знаний и характеристик, изучения процессов развития, установления ...

Аналитическое дешифрование космических снимков

Скачать

40601

0

0

... возраста определяют (по снимкам высокого разрешения) на основе микроструктуры полога насаждений и их статистических характеристик; остальные таксационные показатели - расчетным путем на основе их взаимосвязей. По космическим снимкам с разрешением на местности 10 м и лучше после определения преобладающей и составляющих пород, типа леса или группы типов леса и класса бонитета, дешифрируют группу ...