ОПЕРАТОРЫ

4. ОПЕРАТОРЫ

Сжатие операторов или, другими словами, представление их в разреженном виде в ортонормированном базисе непосредственно влияет на скорость вычислительных алгоритмов.

Нестандартная форма оператора Т с ядром K(x,y) достигается вычислением следующих выражений:

(4.1)

(4.2)

   (4.3)

4.1 Оператор d/dx в вейвлетном базисе

Нестандартные формы некоторых часто используемых операторов могут быть вычислены явно. Построим нестандартную форму оператора d/dx. Матричные элементы , ,  матриц , ,  и  матрицы , где i, l, jÎ Z для оператора d/dx легко вычисляются как

 (4.4)

 (4.5)

  (4.6)

(4.7)

где

(4.8)

(4.9)

 (4.10)

(4.11)

Кроме того, используя (1.8) и (1.19), имеем

(4.12)

 (4.13)

 (4.14)

Таким образом представление d/dx полностью определяется величинами  или, другими словами, отображением d/dx на подпространство V₀.

Предложение 4.1. 1. Если существует интеграл (4.11), тогда коэффициенты , lÎ Z в (5.8) удлвлетворяют следующей системе линейных алгебраических уравнений:

 (4.15)

(4.16)

где

(4.17)

2. Если , тогда система (4.15)-(4.16) имеет единственное решение с конечным числом ненулевых , а именно с  и .

Замечание. Если М=1, тогда система (4.15)-(4.16) имеет единственное решение, но интеграл (4.11) может не быть абсолютно сходящимся. Для базиса Хаара () ,  мы получаем простейший конечный дифференциальный оператор .

Замечание 2. Заметим, что выражения (4.12) и (4.13) для  и  () могут быть упрощены с помощью смены порядка суммирования в (5.10) и (5.11) и введения коэффициентов корреляции ,  и . Выражение для  особенно просто: .

Для доказательства Предложения 4.1 можно обратиться к [2].

Для решения системы (4.15)-(4.16) можно также воспользоваться итерационным алгоритмом. Начать можно с и , а дальше итерировать, используя (4.15) для вычисления .

4.2 Оператор dⁿ/dxⁿ в вейвлетном базисе

 

Так же как и для оператора d/dx, нестандартная форма оператора dⁿ/dxⁿполностью определяется своим отображением на подпространство V₀, т.е. коэффициентами

, lÎ Z, (4.18)

если интеграл существует.

Предложение 4.2. 1. Если интеграл в выражении (4.18) существует, тогда коэффициенты , lÎ Z удовлетворяют следующей системе линейных алгебраических уравнений

(4.19)

(4.20)

где дано в формуле (4.17).

2. Пусть M ≥ (n+1)/2, где М – число исчезающих моментов. Если интеграл в (4.18) существует, тогда система (4.19)-(4.20) имеет единственное решение с конечным числом нулевых коэффициентов , а именно  для . Также для четных n

(4.21)

 (4.22)

 (4.23)

а для нечетных n

(4.24)

(4.25)

Замечание 3. Если M ≥ (n+1)/2, тогда решение линейной системы в Предложении 2 может существовать, когда интеграл в (4.18) не является абсолютно сходящимся.

       Интегральные уравнения второго рода

 

Линейное интегральное уравнение Фредгольма есть выражение вида

,

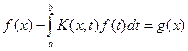где ядро , а неизвестная функция f(x) и функция в правой части , . Для простоты будем рассматривать интервал и введём следующее обозначение для всех  и :

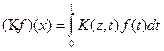
Предположим, что {φ₁, φ₁,…} – ортонормальный базис для ; ядро представимо в этом базисе в следующем виде:

где коэффициенты K_ij вычисляются по формуле

,

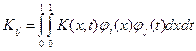Аналогично функции f и g представимы в виде

, ,

где коэффициенты f_i и g_i вычисляются по формулам:

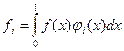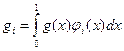, , i=1,2,…

Интегральное уравнение в этом случае соответствует бесконечной системе уравнений

, i=1,2,…

Представление ядра может быть урезано до конечного числа слагаемых, что приводит к представлению интегрального оператора R:

, , ,

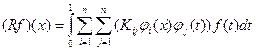который аппроксимирует K. Тогда интегральное уравнение аппроксимируется системой n уравнений с n неизвестными:

, i=1,2,…,n

ПРИЛОЖЕНИЕ 1

function [a,r]=dif_r(wname)

[LO_D,HI_D,LO_R,HI_R] = wfilters(wname);

% вычисление коэффициентов a_2k-1

len=length(LO_D);

a=zeros(len-1,1);

for k=1:len-1;

for i=0:len-2*k;

a(2*k-1)=a(2*k-1)+2*LO_D(i+1)*LO_D(i+2*k);

end;

end;

% вычисление коэффициентов r_l

f=zeros(len-2,1);

f(1)=-1/2;

R=zeros(len-2);

for l=len-2:-1:2;

R(l,l)=-1;

if (2*l<=len-2)

R(l,2*l)=2;

end;

for n=1:2:len-1;

if (abs(2*l-n)<len-2);

if ((2*l-n)<0);

R(l,abs(2*l-n))=-a(n)+R(l,abs(2*l-n));

else

R(l,2*l-n)=a(n)+R(l,2*l-n);

end;

end;

if (abs(2*l+n)<len-2);

if ((2*l+n)<0);

R(l,abs(2*l+n))=-a(n)+R(l,abs(2*l+n));

else

R(l,2*l+n)=a(n)+R(1,2*l+n);

end;

end;

end;

end;

for j=1:len-2;

R(1,j)=j;

end;

r=inv(R)*f;

ПРИЛОЖЕНИЕ 2

function [al, bet, gam]=difcoef(wname,N)

% извлечение коэффициентов r_l

[LO_D,HI_D,LO_R,HI_R] = wfilters(wname);

[a,r]=dif_r(wname);

L=length(LO_D);

% вычисление значений α_l, β_l, γ_l

J=length(r):-1:1;

R=[-r(J);0; r];

K=L+1;

al=zeros(2*L+1,1);

bet=al;

gam=al;

for i=-L+1:L+1;

for k=L+1:2*L;

for k1=L+1:2*L;

if(((2*i+k-k1+L)<length(R)+1)&&((2*i+k-k1+L)>0))

al(i+L)=HI_D(k-L)*HI_D(k1-L)*R(2*i+k-k1+L)+al(i+L);

bet(i+L)=HI_D(k-L)*LO_D(k1-L)*R(2*i+k-k1+L)+bet(i+L);

gam(i+L)=LO_D(k-L)*HI_D(k1-L)*R(2*i+k-k1+L)+gam(i+L);

end;

end;

end;

end;

ПРИЛОЖЕНИЕ 3

1.    Вейвлет Добеши с M=2.
a₁=1.1250 a₃=-0.1250
r₁=-0.6667 r₂=0.0833

2.    Вейвлет Добеши с M=3.
a₁=1.1719 a₃=-0.1953 a₅=0.0234

r₁=-0.7452 r₂=0.1452 r₃=-0.0146 r₄=-0.0003

3.    Вейвлет Добеши с M=4.
a₁=1.19628906249870 a₃=-0.23925781249914
a₅=0.04785156250041 a₇=-0.00488281249997

r₁=-0.79300950497055 r₂=0.19199897079726 r₃=-0.03358020705113

r₄= 0.00222404967066 r₅=0.00017220619000 r₆=-0.00000084085054

4.    Вейвлет Добеши с M=5.
a₁=1.21124267578280 a₃=-0.26916503906311 a₅=0.06921386718738

a₇=-0.01235961914130 a₉=0.00106811523422

r₁=-0.82590601185686 r₂=0.22882018706986 r₃=-0.05335257193327

r₄=0.00746139636621 r₅=-0.00023923581985 r₆=-0.00005404730164

r₇=-0.00000025241171 r₈=-0.00000000026960