Навигация
5. Вейвлет Добеши с M=6.
a1=1.22133636474683 a3=-0.29079437255810 a5=0.08723831176674
a7=-0.02077102661228 a9=0.00323104858448 a11=-0.00024032592766
r1=-0.85013666156022 r2=0.25855294414318 r3=-0.07244058999853
r4=0.01454551104340 r5=-0.00158856154379 r6=0.00000429689148
r7=0.00001202657519 r8=0.00000042069120 r9=-0.00000000289967
r10=0.00000000000070
6. Вейвлет Койфмана с M=2.
a1=1.20035616471068 a3=-0.24753371156550 a5=0.05401594511476
a7=-0.00724698442340 a9=0.00043220193586 a11=-0.00002361577240
r1=-0.80177838961957 r2=0.20214744976459 r3=-0.03943577686925
r4=0.00404789045961 r5=-0.00008445623632 r6=0.00000255044096
r7=0.00000088836508 r8=0.00000000237860 r9=-0.00000000002099
r10=0.00000000000000
7. Симлет с M=2.
a1=1.12499999999971 a3=-0.12499999999971
r1=-0.66666666666616 r2=0.08333333333308
8. Симлет с M=3.
a1=1.17187500000666 a3=-0.19531250000432 a5=0.02343749999766
r1=-0.74520547946903 r2=0.14520547945865 r3=-0.01461187214494
r4=-0.00034246575336
9. Симлет с M=4.
a1=1.19628906249990 a3=-0.23925781249985 a5=0.04785156249993
a7=-0.00488281249998
r1=-0.79300950497424 r2=0.19199897079876 r3=-0.03358020705098
r4=0.00222404967071 r5=0.00017220619000 r6=-0.00000084085054
ПРИЛОЖЕНИЕ 4
1. Вейвлет Добеши с M=2.
| α-3=-0.00520833333331 | β-3 =-0.00139556871057 | γ-3=0.01943776462271 |
| α-2=0.04687500000004 | β-2=0.02222890204378 | γ-2=-0.04027109795592 |
| α-1=0.71874999999873 | β-1=-0.03887552924536 | γ-1=0.00279113742108 |
| α1=-0.71874999999873 | β1=-0.00279113742108 | γ1=0.03887552924536 |
| α2=-0.04687500000004 | β2=0.04027109795592 | γ2=-0.02222890204378 |
| α3=0.00520833333331 | β3=-0.01943776462271 | γ3=0.00139556871057 |
2. Вейвлет Добеши с M=3.
| α-5= -0.00000401327055 | β-5 =0.00000042496289 | γ-5=-0.00003790058109 |
| α-4=0.00173507063342 | β-4=-0.00018594182937 | γ-4= 0.01618803080395 |
| α-3= -0.01438088613327 | β-3= 0.00249383057321 | γ-3= -0.05023776816965 |
| α-2= 0.09779091752885 | β-2=-0.02225975249164 | γ-2=0.03807446337594 |
| α-1=0.84450449488848 | β-1=0.05176823864378 | γ-1=0.02782997442973 |
| α1= -0.84450449488848 | β1= -0.02782997442973 | γ1=-0.05176823864378 |
| α2=-0.09779091752885 | β2= -0.03807446337594 | γ2= 0.02225975249164 |
| α3= 0.01438088613327 | β3= 0.05023776816965 | γ3= -0.00249383057321 |
| α4= -0.00173507063342 | β4=-0.01618803080395 | γ4=0.00018594182937 |
| α5=0.00000401327055 | β5=0.00003790058109 | γ5=-0.00000042496289 |
Вейвлет Добеши с M=4.
| α-7=0.00000000205286 | β-7 =0.00000000009443 | γ-7=-0.00000004462725 |
| α-6=-0.00000544992677 | β-6 =-0.00000025123058 | γ-6=0.00011822433115 |
| α-5=-0.00041543477135 | β-5 =-0.00001769213018 | γ-5=0.00969983443149 |
| α-4=0.00432716179594 | β-4=0.00030224225713 | γ-4= -0.04151919818136 |
| α-3=-0.02134228538239 | β-3=-0.00242879427312 | γ-3= 0.05677199535135 |
| α-2=0.14516544960962 | β-2=0.01699891329704 | γ-2=-0.00862627283270 |
| α-1=0.93050197130889 | β-1=-0.04758076037403 | γ-1=-0.04917088083201 |
| α1=-0.93050197130889 | β1= 0.04917088083201 | γ1=0.04758076037403 |
| a2=-0.14516544960962 | β2= 0.00862627283270 | γ2=-0.01699891329704 |
| a3=0.02134228538239 | β3= -0.05677199535135 | γ3=0.00242879427312 |
| α4=-0.00432716179594 | β4=0.04151919818136 | γ4=-0.00030224225713 |
| a5=0.00041543477135 | β5=-0.00969983443149 | γ5=0.00001769213018 |
| a6=0.00000544992677 | β6=-0.00011822433115 | γ6=0.00000025123058 |
| α7=-0.00000000205286 | β7= 0.00000004462725 | γ7=-0.00000000009443 |
3. Симлет с M=2.
| α-3=-0.00520833333331 | β-3 =-0.00139556871057 | γ-3=0.01943776462271 |
| α-2=0.04687500000004 | β-2=0.02222890204378 | γ-2=-0.04027109795592 |
| α-1=0.71874999999873 | β-1=-0.03887552924536 | γ-1=0.00279113742108 |
| α1=-0.71874999999873 | β1=-0.00279113742108 | γ1=0.03887552924536 |
| α2=-0.04687500000004 | β2=0.04027109795592 | γ2=-0.02222890204378 |
| α3=0.00520833333331 | β3=-0.01943776462271 | γ3=0.00139556871057 |
ЛИТЕРАТУРА
1. Beylkin G. Wavelets and Fast Numerical Algorithms
2. Beylkin G. Wavelets, Multiresolution Analysis and Fast Numerical Algorithms
3. Beylkin G. In The Representation.of Operators in Bases of Compactly Supported Wavelets
4. Bradley K. Alpert A Class of Bases in L2 for the Sparse Representation of Integral Operators
5. Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их использование // Успехи физических наук – 2001, №5. – С.465-500
Похожие работы
... функции j и y и, таким образом, многомасштабный анализ. Кроме того, в правильно построенных алгоритмах значения функций j и y почти никогда не вычисляются. Благодаря рекурсивному определению вейвлетного базиса, все операции проводятся с квадратурными зеркальными фильтрами H и G, даже если в них используются величины, связаные с j и y. 2. Быстрое вейвлет-преобразование После того, как вычислены ...
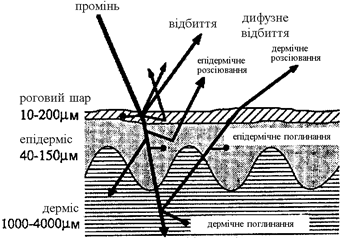
... ів у буферний ЗП контролера клавіатури та дисплея. Але під час виконання роботи був знайдений більш ефективний метод для аналізу пульсової хвилі – вейвлет-аналіз, якому і присвячений наступний розділ. 3. СУТНІСТЬ ВЕЙВЛЕТ-АНАЛІЗУ Вейвлет-перетвореня сигналів є узагальненням спектрального аналізу, типовий представник якого - класичне перетворення Фур'є. Застосовувані для цієї мети базиси ...
0 комментариев