А) При растяжении (сжатии) в p раз (p>0, p¹1) вдоль оси 0X относительно 0Y точка (x; y) переходит в точку (px; y);

3. а) При растяжении (сжатии) в p раз (p>0, p¹1) вдоль оси 0X относительно 0Y точка (x; y) переходит в точку (px; y);

б) При растяжении (сжатии) в q раз (q>0, q¹1) вдоль оси 0Y относительно 0X точка (x; y) переходит в точку (x; qy);

Применительно к графикам функций эти свойства дают те конкретные геометрические преобразования (табл. 1), использование которых позволяет из известного графика функции y=f(x) строить графики других функций (рис. 1 - 11).

Таблица №1

Рассмотрим несколько примеров построения графиков функций:

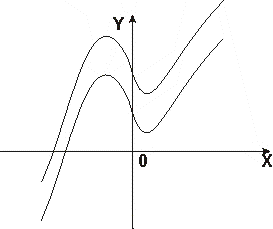Пример 1. График функции y=2x-3 получается из графика y=2x при помощи параллельного переноса его вдоль оси 0Y вниз на отрезок длины 3.

Переписав 2x-3 в виде 2(x-3/2), замечаем, что график функции  y=2(x-3/2) можно получить из графика функции y=2x при помощи

параллельного переноса его вдоль оси 0X вправо на отрезок длины 3/2 (рис. 12).

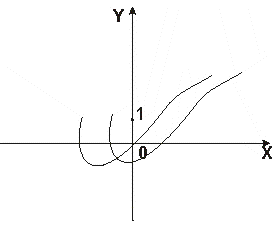
Пример 2. График функции y=4x²получается из графика функции y= x² растяжением последнего в 4 раза вдоль оси 0Y относительно оси 0X. Переписав 4x² в виде (2x)², замечаем, что график функции y= x²можно получить из графика функции y= x²сжатием последнего в 2 раза вдоль оси 0X относительно оси 0Y (рис. 13).

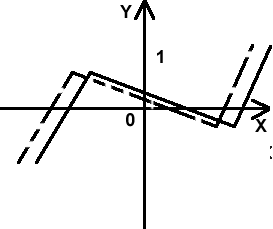
Пример 3. График функции y= 2^x-3 получается из графика y= 2^x при помощи параллельного переноса его вдоль оси 0X вправо на отрезок длины 3.

Переписав 2^x-3 в виде(1/8)*2^x, замечаем, что график функции y=(1/8)*2^x можно получить из графика функции y=2^xсжатием последнего в 8 раз вдоль оси 0X (рис. 14).

Пример 4. Построить график функции:

y=1/2arctg(i/4-x)

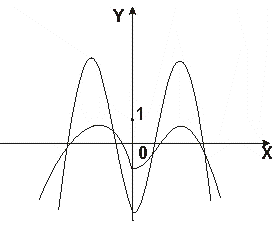Решение: построение графика данной функции может быть проведено по следующей схеме (рис. 13):

arctg ® arctg(-x) ® 1/2arctg(-x) ® 1/2arctg(-(x-1/4)).

Пример 5. Построить график функции:

y=ax²+bx+c, a¹0.

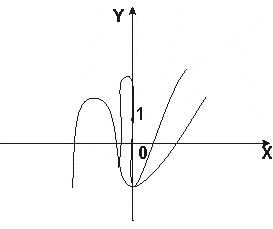Решение: квадратный трехчлен ax²+bx+c можно записать в виде a(x+(b/2a))²+(4ac-b²)/4a. Отсюда видно, что график функции y=ax²+bx+c, получается из параболы y=x² по следующей схеме:

x²® ax²® ax²+(4ac- b²)/4a ® a(x+b/(2a))²+(4ac-b²)/4a

т.е. для построения графика y=a x²+bx+c надо:

1.     Растянуть в |а | раз, если |а | >1 (сжать |1/а | раз, если |а | <1), вдоль оси0X график функции y=x² (с возможным последующим отображением полученного графика функции y=|a| x² относительно оси 0Y, если а<0).

2. 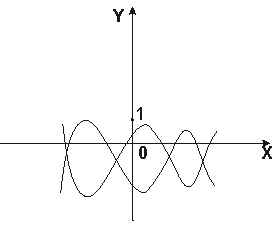    Параллельно перенести вдоль оси 0Y на отрезок длины |(4ac- b²)/4a| вверх (вниз) график функции y=ax², если величина (4ac- b²)/4a положительна (отрицательна).

3.     Полученный после предыдущего преобразования график параллельно перенести вдоль оси 0X на отрезок длины |b/2a| вправо, если b/2a<0, и влево, если b/2a>0.

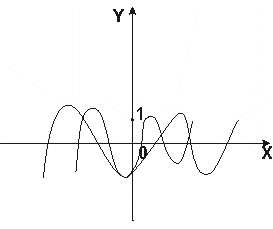
Пример 6. Построить график функции:

y=| x²-5x+6|

Решение: построим график функции y=x²-5x+6

x² ®(x-5/2)² ®(x-5/2)² -1/4= x² -5x+6

На рисунке изображен график функций y=| x²-5x+6|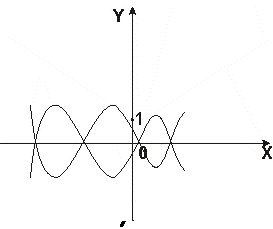

Иногда функция, график которой должен быть построен, представляется как сумма двух простейших функций, графики которых нам знакомы или легко могут быть построены. В этом случае можно применить приём графического сложения ординат этих графиков (для краткости говорят просто о сложении графиков.) покажем этот приём на примерах.

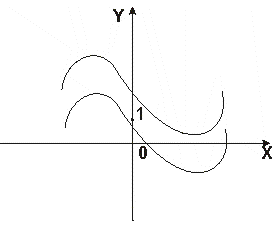
Пример 1. Построить график функций y=x³+2x+2.

Решение: можно представить данную функцию как сумму функций y=x³ и y=-2x+2, графики которых нам хорошо знакомы. Они изображены на рис. 16 тонкими линиями: это прямая y=-2x+2 и кубическая парабола y=x³. Далее производится суммирование ординат: к ординатам точек кубической параболы прибавляются (с учетом знака!) ординаты точек прямой. При выполнении этой операции удобно пользоваться мерительным циркулем; следует использовать наиболее важные и характерные точки каждого из графиков (в нашем примере – вершину O(0; 0) параболы, точки пересечения прямой с осями и т.д.). Итогом построения служит график, показанный жирной линией. Мы можем много сказать о функции: она имеет максимум и минимум, обращается в нуль в одной точке и т.д. Положение этих характерных точек её графика мы могли бы найти приближенно по чертежу.

Пример 2. Построить график функций y=2^ч-2x.

Решение: график данной функции можно получить сложением графиков показательной функции y=2^xи линейной функции y=-2x. Это сделано на рис. 17. График пересекает ось OX в точках x=1, x=2, являющихся нулями функции y=2^ч-2x.

Обратим ещё внимание на то, что прямая y=-2x является асимптотой графика (т.к. при x, стремящимся к минус бесконечности, разность между значениями функций y=2^ч-2x и y=-2x стремится к нулю). Из построения видно, что функция имеет точку минимума, найти её точное положение для нас затруднительно.

Пример 3. Построить график функций y=x²-x⁴.

Решение: график может быть построен вычитанием ординат графика y=x⁴  из ординат графика y=x² (рис. 18). В данном случае полезно дополнить это построение некоторым общим исследованием свойств функции y=x²-x⁴. Ясно, что функция определена для всех значений x и является четной. Она обращается в нуль при x=0, x= ±1. Как видно из построения графика методом вычитания, следует ожидать у функции наличия двух точек максимума. В данном случае их нетрудно найти; преобразуем выражение функции:

y=x²-x⁴=1/4-(1/4- x²+x⁴)=1/4-( x²-1/2) ² .

Теперь видно, что наибольшее значение y=1/4 функция имеет при х=±1/Ö2. Точка x=0 является точкой минимума данной функции (но значение функции в этой точке, равное нулю, не есть её наименьшее значение).

(книга 2)

Используя геометрические преобразования, рассмотренные выше, в их различных комбинациях, можно построить и графики более сложных функций.

Пример1. Построить график функций

y= |||x | - 1| -2|

Решение: график данной функции можно построить по графику функции y=||x|-1|, если последний параллельно перенести вдоль оси 0Y вниз на отрезок длины 2, а затем эту часть полученного графика функции y= ||x | - 1| -2, которая расположена в нижней полуплоскости, симметрично отобразить относительно оси 0X. График функции y= ||x | - 1| можно построить по графику функции y= |x| если последний параллельно перенести вдоль оси 0Y вниз на отрезок длинны 1, а затем ту часть полученного графика функции y= |x| - 1, которая расположена в нижней плоскости, симметрично отобразить относительно оси 0X.

Таким образом, график заданной функции может быть построен согласно схеме: x®|x|®|x|-1®||x|-1|® ||x|-1|-2®|||x|-1|2|

§3. Применение производной

к построению графика функции

Графики функций строятся по точкам. Обычно из уравнения y=f(x) находят несколько точек графика функций y=f(x) и соединяют эти точки плавной кривой. Однако при таком методе легко пропустить какие-то особенности графика и допустить ошибку в построении.

Для построения графика функции нужно исследовать её свойства. Прежде всего надо найти область определения функции, а потом исследовать функцию на честность и периодичность. Т.к. график четной функции симметричен относительно оси Оу, а график нечетной - относительно начала координат, то для четных и нечетных функций можно ограничится исследованием их свойств лишь при х³0. Если периодическая и Т – её основной период, то можно ограничится исследованием свойств функции на промежутке длинны Т.

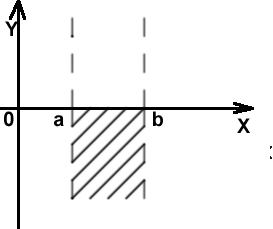Далее полезно найти точки пересечения графика с осями координат и определить интервалы знакопостоянства функции. Дело в том , что если, скажем, на интервале (a; b) функция y=f(x) принимает только положительные значения, то график её на этом интервале лежит выше оси Ох. Значит, часть плоскости, лежащею под указанным интервалом, можно заштриховать – там графика нет. Эта часть исследования позволяет указать области, где может лежать график функции. После этого можно изучить поведения функции на границах области определения, установить характер точек разрыва (если они есть), найти асимптоты. Наконец следует найти промежутки возрастания и убывания функции и исследовать её на экстремум.

Подводя итог всему сказанному выше, получаем следующую схему исследования свойств функции и построения ее графика.

1.  Найти область определения функции,

2.  Исследовать функцию на четность.

3.  Исследовать функцию на периодичность.

4.  Найти точки пересечения графика с осями координат.

5.  Определить промежутки знакопостоянства.

6.  Исследовать функцию на границах области. Найти асимптоты.

7.  Исследовать функцию на экстремум.

8.  Составить таблицу значений функции для некоторых значений аргумента.

9.  Используя все полученные результаты ,построить график функции.

Пример 1. Построить график функции y= x⁴-2 x²-8.

Решение. 1.Функция определена при любом значении  x,т.е. D=(f)=R.

2. Так как область определения функции - симметричное множество и f(-x)=f(x),то функция четна .Следовательно график функции симметричен относительно оси Оy и для дальнейшего исследования можно ограничится промежутком [0,+ ]. Но в данном примере мы этого делать не будем.

3Функция непериодическая.

4.   Найдем точки пересечения графика с осью Ох. Для этого решим уравнение x⁴- x²-8=0. Пологая u= x²,получим квадратное уравнение u²- u-8=0. Пологая u= x², получим квадратное уравнение u²- u-8=0, имеющее корни 4 и –2. Из уравнения x²=4 находим х=2, х=-2, уравнение x²=-2 не имеет решений. Мы нашли две точки пересечения с осью Ох:(2;0) и (-2;0).

С осью Оу график функции пересекается в точке(0;-8).

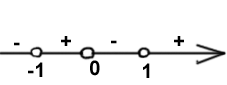
5.     Найдем интервалы знакопостоянства функции. Заданная функция не прерывна на всей числовой прямой обращается в 0 в точках 2 и –2. Значит, в промежутках (- ,-2). (-2;2) и (2; ) она сохраняет постоянный знак Чтобы определить знак функции на каждом из указанных промежутков, достаточно взять по одной “пробной” точке из каждого промежутка.

Имеем –100 (- ,2), f(-100)=(-100)⁴-2(-100)²-8>0. Значит, f(x)>0 в промежутке (- ; -2). Далее, 0Î(-2; 2), f(0)=-8<0. Поэтому f(x)<0 в промежутке(-2; 2). Наконец, 100Î(2; + ), f(100)=f(-100), а выше мы видели, что f(-100)>0. Следовательно, f(100)>0, а потом f(x)>0 в промежутке (2; + ).

На рисунке представлена геометрическая иллюстрация тех сведений о графике, которыми мы располагаем к настоящему моменту. Заштрихованы те участки координатной плоскости, где графика нет, отмечены известные точки(0; -8), (2; 0), (-2; 0). Это – ответ на вопрос, где расположен график. Дальнейшее исследование позволяет ответить на вопрос, как строить график.

6) Изучим поведение функции вблизи границ области определения. Поскольку D(f)=(- ; + ), такими «границами»можно считать - и + . преобразовав выражение x⁴-2x²-8 к виду x²-( x²-2-8/ x²), замечаем, что если х®- или х®+ , то у®+ .

Асимптот график не имеет.

7) Исследуем функцию на экстремум; имеем

y’=4 x³-4x=4x(x-1)(x+1)

Прировняв производную нулю, находим три корня: 0, 1, -1. Эти точки разбивают числовую прямую на промежутки (- ; -1), (-1;0), (0;1), (1; + ). Если х>1, то у'>0, а в остальных промежутках знаки чередуются справа на лево, смотри рисунок.

Составим таблицу:

x	- <x<-1	-1	-1<x<0	0	0<x<1	1	1<x<+
f’(x)	-	0	+	0	-	0	+
f(x)	Убыв.	-9 min	Возр.	-8 max	Убыв.	-9 min	Возр.

Итак, в точках (-1; -9) и (1; -9) функция имеет минимум, а в точке (0; -8) - максимум.

8) Составим таблицу значений функции для некоторых значений аргумента, включая те, что были уже отмечены в ходе исследования:

X	-2	-1	0	1	2	-2,5	2,5
Y	0	-9	-8	-9	0	»6	»6

9) Строим график функции y= x⁴-2 x²-8.

 

 

 

 

 

 

 

 

 

 

 

Пример 2. Построить график функции y=( x²-1)/x.

Решение:

1.   Функция не определена только в точке х=0, т.е. D(f)=(- ; 0)È(0; + ).

2.  Множество D(f) является симметричным; кроме того f(-х)=((-х)²-1)/-х=-(x²-1)/-х=-f(х). Значит, y=f(x) – нечетная функция. Поэтому график симметричен относительно начала координат и для дальнейшего исследования можно ограничится промежутком (0; + ), что мы и сделаем.