Навигация
Функция непериодическая
3. Функция непериодическая.
4. Найдем точки пересечения графика с положительным лучом оси Ох. Из уравнения ( x2-1)/x=0 находим x=1 (корень х=-1 пока не принемаем во внимание). Итак, точка пересичения с осью Ох – точку (1; 0).
С осью Оу график не пересекается, т.к. точка х=0 не принадлежит к области определения функции: 0 D(f).
5. Находим промежутки знакопостоянства: (0; 1) и (1; + ). В первом из них f(x)<0, во втором f(x)>0/
На рисунке представлена геометрическая иллюстрация тех сведений о графике, которыми мы располагаем к настоящему моменту.
6. Изучим поведение функции вблизи границ области определения, т.е. вблизи точки ноль и при х®+ . Если х®0 (напомним, что мы рассматриваем случай где х>0), то (x2-1)/x®. Если же х®+ , то ( x2-1)/x=х-1/х®+ .
Прямая х=0 является вертикальной асимптотой. Далее, т.к. степень числителя выражается (x2-1)/x на единицу больше степени знаменателя, то должна существовать и наклонная асимптота. В самом деле, поскольку (x2-1)/x=х-1/х и 1/х стремятся к нулю при х®+ , наклонной асимптотой служит прямая у=х.
7. Исследуем функцию на экстремум; имеем
y’=((x2-1)/x)’=([-1/x)’=1+1/ x2.
Замечаем, что у’>0при любых х. Значит на луче (0; + ) функция возрастает и экстремумов не имеет.
8. Составим таблицу значения функции:
| x | 1 | 0.5 | 0.25 | 2 | 3 | 4 |
| y | 0 | -1.5 | -3.75 | 1.5 | 2.67 | 3.75 |
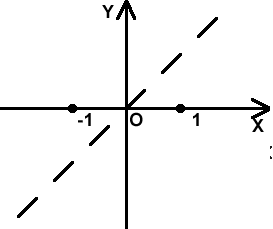
9. отметив найденные точки на координатной плоскости и учитывая результаты исследования, строим ветвь графика при х>0, смотри рисунок.
Т.к. график функции y=(x2-1)/x, симметричен относительно начала координат, то добавив к построенной ветви симметричную ей относительно начала координат, получим искомый график.
10. Глава 3. ФОРМИРОВАНИЕ УМЕНИЯ
САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПРИ ИЗУЧЕНИИ ФУНКЦИЙ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ
В настоящее время каждый учитель математики ставит перед собой задачу не только сообщить школьникам определенную сумму знаний, наполнить их память некоторым набором фактов и теорем, но и научить учащихся думать, развить их мысль, творческую инициативу, самостоятельность. Привитие ученикам навыков самостоятельной работы, умения ориентироваться в поступающей информации, умения самостоятельно пополнять свои знания — это сложный и длительный процесс, требующий специально организованной и целенаправленной работы учителя, в которой, так же как и в любой другой работе. выделяются определенные этапы.
Среди совокупности умений и способов деятельности, которыми овладевают учащиеся при изучении математики, существуют такие, которыми должен прочно овладеть каждый ученик, для того чтобы учебный процесс протекал нормально.
Изучению функций и их свойств посвящена значительная часть курса алгебры. И это не случайно. Понятие функции имеет огромное прикладное значение. Умения, приобретаемые школьниками при изучении функций, имеют прикладной и практический характер. Они широко используются при изучении, как курса математики, так и других школьных предметов — физики, химии, географии, биологии, находят широкое применение в практической деятельности человека. От того, как усвоены учащимися соответствующие умения, зависит успешность усвоения многих разделов школьного курса математики.
При выделении обязательных задач по теме «Функции», следует ориентироваться на то, что обучение в VI—VIII классах представляет собой не завершающий, а промежуточный этап в системе математического образования каждого школьника: На базе полученной им математической подготовки строится его дальнейшее обучение. Поэтому для определения реально необходимого уровня сформированности умений по каждому вопросу, в первую очередь, следует проанализировать характер и уровень использования этих умений на следующих ступенях обучения. Кроме того, важное значение имеет характер применения математических знаний учащихся в смежных школьных предметах.
Применительно к функциональному материалу естественным представляется проанализировать характер его применения в курсе алгебры и начал анализа, геометрии, а также школьного курса физики. Анализ теоретического и задачного материала этих курсов позволяет выделить две группы умений, за формированием которых следует тщательно следить при изучении всех видов конкретных функций,— умения работать с формулой, задающей функцию, и умения работать с графиком этой функции.
К умениям работать с формулами относятся "следующие.
Если функции вида y=kx+b, у=k/x, y=ax2+bx+c, у=х3, y=Öx заданы формулами с конкретными значениями параметров, то учащиеся должны уметь:
— указать область определения функции;
— вычислить значение функции, соответствующее заданному значению аргумента;
—вычислить значение аргумента, при котором функция принимает заданное значение;
— определить, принадлежит ли точка с заданными координатами графику функции,
Все эти умения широко используются в разной деятельности учащихся, входят в качестве составных в большое число других умений. Так, например, умение найти значение функции при заданном значении аргумента используется при построении графиков функций, нахождении наибольшего и наименьшего значений функции, вычислении пределов функций, интегралов и др. В курсе физики оно используется практически при изучении всех вопросов. Это так называемые вычисления по формулам: длины пройденного пути при равномерном прямолинейном движении, силы тока в проводнике, координаты тела при равномерном и равноускоренном движении и т.. д. Умение записать нужное равенство, зная, что заданная точка принадлежит графику функции (а также графику уравнения), требуется учащимся, например, в курсе геометрии при выводе уравнений прямой, окружности, плоскости.
Важнейшее значение в функциональной подготовке учащихся - имеет формирование графических умений. График — это средство наглядности, широко используемое при изучении многих вопросов в школе.
График функции выступает основным опорным образом при формировании целого ряда понятий — возрастания и убывания функции, четности и нечетности, обратимости функции, понятия экстремума. Без четких и сознательных представлений учащихся о графике невозможно привлечение геометрической наглядности при формировании таких центральных понятий курса алгебры и начал анализа, как непрерывность, производная, интеграл. Поэтому заниматься формированием графических представлений в старших классах уже поздно. К этому времени у учащихся должны быть выработаны прочные умения как в построении, так и в чтении графиков функций. Прежде всего учащиеся должны уметь свободно строить графики основных функций:
y=kx+b, у=k/x, y=ax2+bx+c, (при конкретных значениях параметров), у=х3, y=Öx
Необходимой базой последующего применения функционального материала являются прочные самостоятельные умения учащихся в чтении графиков функций. Они должны уметь уверенно и свободно отвечать с помощью графика на целый ряд вопросов: ,
— по заданному значению одной из переменных х или у определить значение другой;
— определять промежутки возрастания и убывания функции;
— определять промежутки знакопостоянства;
— для квадратичной функции указывать значение аргумента, при котором функция принимает наибольшее (наименьшее) значение, а также определять это значение.
Ученики должны хорошо представлять себе вид графиков некоторых функций, а именно: у=х, у=—х, у=х2, и уметь без специального построения по точкам показать их расположение в координатной плоскости.
И наконец, учащиеся должны применять графики изученных перечисленных выше функций для графического решения уравнений, систем уравнений, неравенств вида f(x)³0.
Достижение„всеми учащимися выделенных результатов обучения требует специальной ориентации процесса обучения, серьезной и тщательной работы учителя по обеспечению такого усвоения. При этом правильно организованная работа по обучению учащихся решать основные типы задач не только не противоречит тезису о развитии самостоятельности учащихся в учебной деятельности, но и способствует такому развитию, закладывает основы обучения школьников обще учебным умениям, умениям самостоятельной работы. Остановимся на некоторых из этих вопросов.
Прежде всего, одним из условий эффективности этой работы является своевременное ознакомление учащихся с основными требованиями к их знаниям и умениям. Это может делаться в различной форме. Приступая к изучению какой-либо функции, целесообразно сообщить учащимся в самом общем виде, какими умениями они должны овладеть в обязательном порядке. Например, начав изучать функцию вида y=ax2+bx+c, можно указать учащимся, что усвоение этого материала будет оценено положительно только в
том случае, если они научатся строить график квадратичной функции и по графику отвечать на некоторые вопросы. В ходе изучения материала следует уточнить требования, конкретизировав их вторую часть. При этом, если имеется такая возможность, полезно указать номера упражнений, отражающих основные требования.
Сформировать прочные умения в построении и чтении графиков функций, добиться, чтобы каждый ученик мог выполнять основные виды заданий самостоятельно, можно только при условии выполнения учащимися достаточного числа тренировочных упражнений. Но было бы большой ошибкой, если бы эта работа ограничивалась только тренировкой. Обоснованность действий, сознательность при их выполнении, внимание к формированию умений обще учебного характера — непременное условие прочности в овладении умениями. Рассмотрим это на примере отработки умения строить графики функций.
Часто приходится наблюдать, особенно в практике работы неопытных учителей, что при формировании этого умения они ограничиваются исключительно тренировочными упражнениями, не уделяя должного внимания овладению понятиями, изучению свойств функций. Результатом является то, что при затрате больших сил и времени учащиеся так и не приобретает умения свободно и уверенно строить графики. Проанализируем один пример. В итоговой контрольной работе по алгебре за курс VI класса учащимся было предложено построить график функции, заданной формулой у=2х—1. Многие учащиеся справились с заданием. Однако среди ошибок были такие, которые свидетельствовали о несформированности не только умения строить график линейной функции, но и строить график вообще. В некоторых работах на рисунке вместо прямой можно было видеть некое подобие параболы или гиперболы. Иногда это была и прямая, но проходящая через другие координатные углы. Ученики, таким образом выполнившие задание, усвоили только одно: для того чтобы построить график функции, надо находить координаты точек, принадлежащих графику. Допущенные в вычислениях ошибки не Позволили им верно выполнить задание, однако проконтролировать себя в ходе его решения они не смогли. Это свидетельствуемо том, что в ходе обучения построению графиков функций акцент делался на механическое повторение способов построения графиков отдельных функций и недооценивалось значение теоретических знаний.
При обучении учащихся построению графиков функций следует ориентироваться не на формальное повторение школьниками отдельных приемов построения графиков, а на сознательное усвоение материала. Необходимо уделять серьезное внимание усвоению соответствующих понятий, изучению свойств функций и формированию на этой основе способов построения графиков.
При изучении всех видов функций построение графика полезно проводить по одному и тому же общему плану, добиваясь от учащихся его непременного соблюдения:
1. по формуле распознать вид функции (линейная, квадратичная и т. д.)
2. вспомнить, что является графиком функции такого вида (прямая, парабола и т. д.)
3. выяснить, исходя из формулы, некоторые характерные особенности этого графика (так как k>0, то угол наклона прямой к оси х острый; так как а<0, то ветви параболы направлены вниз;
4. приступать к построению графика по точкам, используя для каждого вида функции свой специфический способ.
При выполнении упражнения всем классом, сопровождающемся построением графика на доске, надо непременно требовать от отвечающего ученика вслух комментировать ход решения, выделяя каждый из этих этапов, не пропуская ни один из них. Такая планомерная работа приводит к тому, что соблюдение этого плана становится привычным для ученика, и каждый ученик самостоятельно обращается к нему при построении любого графика.
Обучаясь построению графиков конкретных функций, ученик обучается составлению определенного плана действий. Приступая к решению поставленной перед ним задачи, ученик не берется за ее выполнение «в лоб», а предварительно намечает исходную идею решения. Иными словами, у него появляется основа для ориентировочных действий. А это, в свою очередь, способствует приобретению навыков самоконтроля. Причем подход к самоконтролю здесь не формальный, в отличие от широко распространенного в практике, когда ученикам, уже выполнившим задание, предлагают:
«Проверьте свое решение». В такой ситуации ученик, как правило, не знает, что ему при этом надо делать и в лучшем случае просто прочитывает свое решение еще раз. Однако ему трудно увидеть ошибки и немудрено, что ошибочное решение часто остается неисправленным. Анализ же условия и обдуманная наметка пути решения на первоначальном этапе более эффективны в плане самоконтроля, так как ученик получает возможность контролировать свои действия на каждом этапе выполнения задания. Так, например, установив, что графиком функции является прямая, ученик уже не станет изображать на рисунке параболу. Зная, что угол наклона прямой к оси х должен быть острым, он насторожится, если у него на рисунке получится тупой угол, и это может заставить его пересмотреть некоторые моменты своего решения. Базу для такого самоконтроля создает твердое знание основного теоретического материала, знание свойств функций.
Для прочного усвоения свойств изучаемых функций необходимо включать специальные упражнения, заставляющие учащихся актуализировать имеющиеся у них знания о функциях, выполнять некоторый перебор знаний с целью выбора нужных в данной ситуации. С этой точки зрения эффективны упражнения на соотнесение графика функции с формулой, задающей эту функцию. Например, после изучения свойств линейной функции можно предложить учащимся задание такого типа: «На рисунке изображены графики линейных функций и приведены формулы, задающие эти функции: y=-0,5x+1; у=3; у=2х+2; y=3x. Установите, какая формула соответствует каждому из представленных графиков». Эти упражнения легко варьировать, увеличивая, например, число приводимых формул, после изучения новых видов функций, включая графики различных функций. Например, предложить учащимся соотнести каждый из графиков, изображенных на рисунке, с формулами:
y=2х—1; у=2х; у=х2; y=3/x; y=х3.
Подобные задания можно выполнять устно при фронтальной работе с классом и письменно в виде самостоятельной работы. В первом случае следует непременно требовать от учащихся обоснования своего выбора. Не отнимая много времени на уроке, эти упражнения приносят существенный эффект и помогают добиться прочных умений. в построении графиков функций.
В заключение отметим, что, хотя работа по обучению учащихся умению самостоятельно решать основные виды задач еще не решает проблемы развития самостоятельности учащихся в целом и ее, конечно, недостаточно для достижения такой цели, все же эта работа является важным этапом в ее достижении. Обучение деятельности по образцу имеет в математике свою специфику, так как в большинстве случаев такая деятельность не сводится к чисто воспроизводящей. Воспроизводится именно способ решения, сама же задача, ее конкретные данные всегда варьируются. При решении любой задачи, при выполнении каждого упражнения ученик осуществляет хотя бы элементарный перенос знаний, актуализирует необходимый способ действий, определяет путь решения. Таким образом, целенаправленная и тщательная работа по организации овладения всеми учащимися необходимым набором умений создает основу для перехода на более высокий уровень самостоятельности, является необходимой базой такого перехода. Кроме того, эта работа не только не противоречит идее развития у учеников общеучебных умений, составляющих основу самостоятельной деятельности каждого ученика, но включает в себя большие возможности в этом плане и, правильно организованная, служит начальным этапом формирования этих умений.
ЛИТЕРАТУРА
1. С.И. Демидова, Л.О. Денищева «Самостоятельная деятельность учащихся при обучении математике»-М:,Просвищение-1985г.-192с.
2. Народное образование№6-1990г.,с.62
3. «Математика в школе»№3-1998г.,с.37
4. «Математика в школе»№2-1999г.,с.53
5. Газета «Математика»№33-1999г.
6. Газета «Математика»№16-1998г.
7. В.В. Вавилов, И.И. Мельников, С.Н. Олехник, П.И. Пасеченко «Задачи по математике. Начало анализа: Справочное пособие» - М:, Наука. Гл. ред. Физ. - мат. лит.,1990-608с.
8. Газета «Математика»№39-1997г.
9. В.Г. Болтянский, Ю.В. Сидоров, М.И, Шабунин, А.Б. Марткович «Математика. Лекции, задачи, решение» - Минск, Издательство»Альфа»-1994г.-638с.
10. Алгебра и начало анализа. Учебник для 10-11 кл. сред. шк./ А.Н. Колмагоров, А.М. Абрамов, Ю.П. Дубницин и д.р.: Под ред. А.Н. Колмагорова-2-е изд.-М.:Просвещение, 1991г.-320с.
11. Алгебра; Учебник для 9 класса средней школы-/Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под ред. .А. Теляковского.–2-е изд.–М.:Просвещение, 1992г.-271с.
12. Дидактические материалы по алгебре и начале анализа для 11 кл. /Б.М. Ивлев, С.М.Саакян, С.И. Шварцбурд. - М.: Просвещение, 1991г. – 192с.
13. Дидактические материалы по алгебре и начале анализа для 9 кл.: Пособие для учителя /Б.М. Ивлев, С.М.Саакян, С.И. Шварцбурд. - 2-е изд. перераб. - М.: Просвещение, 1987г.
14.Программа общеобразовательных учреждений «Математика» - М; Просвещение, 1994г.
15. «Математика в школе» №6 – 1996г. 21с.
16. «Математика в школе» №5 – 1999г. 2с.
17. А.Д. Мышкис «Лекции по высшей математике» - М;, 1969г.
18. В.В. Зайцев, В.В. Рыжков, М.И. Сканави, «Элементарная математика» - М;, Наука 1976г., 591с.
19. Г.И. Багатырев, О.А. Боковнев, «Математика для подготовительных курсов техникумов»
20. Я.Б. Зельдович «Высшая математика для начинающих и ее приложение к физике.» М.,Физматгиз-1963г.-560с.
21. В.А. Слабодская «Краткий курс высшей математики. Изд. 2-е,переработ. и доп. Учеб. Пособие для втузов. М., Высшая школа-1969г.-544с.
22. А.Я. Симонов, Д.С. Бакаев, А.Г. Эпельман «Система тренировочных задач и упражнений по математике» М.:Просвещение,1991г.-208с.
23. П.П. Коровкин «Математический анализ» М.: Просвещение, 1974г.-464с.
Похожие работы
... работа оказывает значительное влияние на глубину и прочность знаний учащихся по предмету, на развитие их познавательных способностей, на темп усвоения нового материала. Практический опыт учителей многих школ показал, что: 1. Систематически проводимая самостоятельная работа (с учебником по решению задач, выполнению наблюдений и опытов) при правильной ее организации способствует получению ...
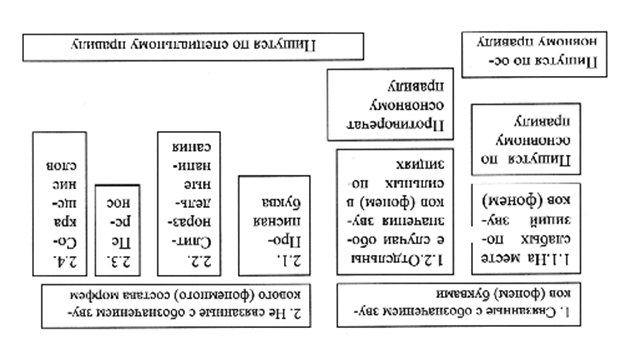
... восприятие. Контролирующий компонент складывается на основе самопроверки написанного в результате сличения воспринимаемых зрительных образов с их следом в памяти. Таким образом, на формирование орфографической зоркости оказывают большое влияние следующие психические процессы: а) активное зрительное и слуховое восприятие, включающее в себя целенаправ ленный анализ; б) логические операции сравнения ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
... эксперимент. В ходе эксперимента подтверждена эффективность данной методики. Так же установлено, что для достижения активизации познавательной деятельности учащихся в процессе обучения технологии необходимо: использовать проблемно- поисковый метод обучения в комплексе с методами стимулирования, контроля, самоконтроля и самооценки. Данная работа может оказаться полезной для учителя применяющего ...
0 комментариев