Навигация
УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ
2. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ
Рассмотрим уравнение первой степени с двумя неизвестными
|
| (3) |
где ![]() и
и ![]() - целые числа, отличные от нуля, а
- целые числа, отличные от нуля, а ![]() - произвольное целое. Будем считать, что коэффициенты
- произвольное целое. Будем считать, что коэффициенты ![]() и
и ![]() не имеют общих делителей, кроме единицы. Действительно, если общий наибольший делитель этих коэффициентов
не имеют общих делителей, кроме единицы. Действительно, если общий наибольший делитель этих коэффициентов ![]() отличен от единицы, то справедливы равенства
отличен от единицы, то справедливы равенства ![]() ,
, ![]() ; уравнение (3) принимает вид
; уравнение (3) принимает вид
|
|
и может иметь целые решения только в том случае, когда ![]() делится на
делится на ![]() . Таким образом, в случае
. Таким образом, в случае ![]() - все коэффициенты уравнения (3) должны делиться нацело на
- все коэффициенты уравнения (3) должны делиться нацело на ![]() , и, сокращая (3) на
, и, сокращая (3) на ![]() , придем к уравнению
, придем к уравнению
|
|
коэффициенты которого ![]() и
и ![]() взаимно просты.
взаимно просты.
Рассмотрим сначала случай, когда ![]() . Уравнение (3) перепишется так:
. Уравнение (3) перепишется так:
|
| (3') |
Решая это уравнение относительно![]() , получим
, получим
|
|
Ясно, что ![]() будет принимать целые значения в том и только в том случае, когда
будет принимать целые значения в том и только в том случае, когда ![]() делится на
делится на ![]() без остатка. Но всякое целое
без остатка. Но всякое целое ![]() , кратное
, кратное ![]() , можно записать в виде
, можно записать в виде
|
|
где ![]() принимает произвольные целые значения
принимает произвольные целые значения ![]() . Подставим это значение
. Подставим это значение ![]() в предыдущее уравнение, тогда
в предыдущее уравнение, тогда
|
|
и мы получаем формулы, содержащие все целые решения уравнения (3'):
|
|
Перейдем теперь к случаю ![]() .
.
Покажем, прежде всего, что для нахождения всех целых решений уравнения (3) достаточно найти какое-нибудь одно его решение, т. е. найти такие целые числа![]() ,
, ![]() , для которых
, для которых
|
|
Т е о р е м а I. Пусть а и b взаимно просты и ![]() - какое-нибудь решение уравнения
- какое-нибудь решение уравнения
|
| (3) |
Тогда формулы
|
| (4) |
при ![]() дают все решения уравнения (3).
дают все решения уравнения (3).
Д о к а з а т е л ь с т в о. Пусть ![]() - произвольное решение уравнения (3). Тогда из равенств
- произвольное решение уравнения (3). Тогда из равенств
|
|
получаем
|
|
Так как ![]() - целое число и числа
- целое число и числа ![]() и
и ![]() взаимно просты, то
взаимно просты, то ![]() должно нацело делиться на
должно нацело делиться на ![]() , т. е.
, т. е. ![]() имеет вид
имеет вид
|
|
где ![]() - целое. Но тогда
- целое. Но тогда
|
|
и получаем
|
|
Таким образом доказано, что всякое решение ![]() имеет вид (4). Остается еще проверить, что всякая пара чисел
имеет вид (4). Остается еще проверить, что всякая пара чисел ![]() , получаемая по формулам (4) при целом
, получаемая по формулам (4) при целом ![]() , будет решением уравнения (3). Чтобы провести та кую проверку, подставим величины
, будет решением уравнения (3). Чтобы провести та кую проверку, подставим величины ![]() ,
, ![]() в левую часть уравнения (3):
в левую часть уравнения (3):
|
|
но так как ![]() -решение, то
-решение, то ![]() и, следовательно,
и, следовательно, ![]() , т.е.
, т.е. ![]() - решение уравнения (3), чем теорема полностью доказана.
- решение уравнения (3), чем теорема полностью доказана.
Итак, если известно одно решение уравнения ![]() , то все остальные решения найдутся из арифметических прогрессий, общие члены которых имеют вид:
, то все остальные решения найдутся из арифметических прогрессий, общие члены которых имеют вид:
![]() ,
, ![]()
![]() .
.
3аметим, что в случае, когда ![]() , найденные раньше формулы решений
, найденные раньше формулы решений
|
|
могут быть получены из только что выведенных формул ![]() ,
, ![]() , если выбрать
, если выбрать ![]() , что можно сделать, так как значения
, что можно сделать, так как значения ![]() ,
, ![]() являются, очевидно, решением уравнения
являются, очевидно, решением уравнения
|
|
Как же найти какое-нибудь одно решение ![]() уравнения (3) в общем случае, когда
уравнения (3) в общем случае, когда ![]() . Начнем с примера.
. Начнем с примера.
Пусть дано уравнение ![]()
Преобразуем отношение коэффициентов при неизвестных.
Прежде всего, выделим целую часть неправильной дроби ![]() ;
; ![]()
Правильную дробь ![]() заменим равной ей дробью
заменим равной ей дробью ![]() .
.
Тогда получим 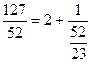 . Проделаем такие же преобразования с полученной в знаменателе неправильной дробью
. Проделаем такие же преобразования с полученной в знаменателе неправильной дробью ![]() .
.
Теперь исходная дробь примет вид: 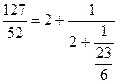
Повторяя те же рассуждения для дроби ![]() получим
получим 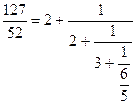 .
.
Выделяя целую часть неправильной дроби![]() , придем к окончательному результату:
, придем к окончательному результату:
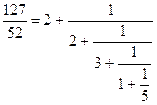
Мы получили выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби - одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем ее из исходной дроби ![]() :
:
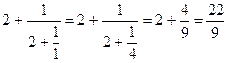 ,
, ![]() .
.
Приведем полученное выражение к общему знаменателю и отбросим его, тогда
![]() .
.
Из сопоставления полученного равенства с уравнением ![]() следует, что
следует, что ![]() ,
, ![]() будет решением этого уравнения и согласно теореме все его решения будут содержаться в прогрессиях
будет решением этого уравнения и согласно теореме все его решения будут содержаться в прогрессиях ![]() ,
, ![]()
![]() .
.
Полученный результат наводит на мысль о том, что и в общем случае для нахождения решения уравнения ![]() надо разложить отношение коэффициентов при неизвестных в цепкую дробь, отбросить ее последнее звено и проделать выкладки, подобные тем, которые были проведены выше.
надо разложить отношение коэффициентов при неизвестных в цепкую дробь, отбросить ее последнее звено и проделать выкладки, подобные тем, которые были проведены выше.
Для доказательства этого предположения будут нужны некоторые свойства цепных дробей.
Рассмотрим несократимую дробь ![]() . Обозначим через
. Обозначим через ![]() частное и через
частное и через ![]() остаток от деления а на b. Тогда получим:
остаток от деления а на b. Тогда получим: ![]() ,
, ![]() .
.
Пусть, далее, ![]() - частное и
- частное и ![]() - остаток от деления
- остаток от деления ![]() на
на ![]() Тогда
Тогда ![]() ,
, ![]() ; точно так же
; точно так же
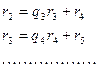
![]()
![]()
Величины ![]() ,
, ![]() ,… называются неполными частными. Приведенный выше процесс образования неполных частных называется алгоритмом Евклида. Остатки от деления
,… называются неполными частными. Приведенный выше процесс образования неполных частных называется алгоритмом Евклида. Остатки от деления ![]() ,
, ![]() ,…удовлетворяют неравенствам
,…удовлетворяют неравенствам
|
| (5) |
т. е. образуют ряд убывающих неотрицательных чисел.
Так как количество неотрицательных целых чисел, не превосходящих b, не может быть бесконечным, то на некотором шаге процесс образования неполных частных оборвется из-за обращения в ноль очередного остатка r. Пусть ![]() - последний отличный от нуля остаток в ряде (5); тогда
- последний отличный от нуля остаток в ряде (5); тогда ![]() и алгоритм Евклида для чисел a и b примет вид
и алгоритм Евклида для чисел a и b примет вид
![]()
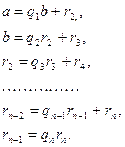 (6)
(6)
Перепишем полученные равенства в виде
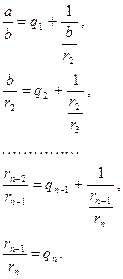
Заменяя значение ![]() в первой строке этих равенств соответствующим значением из второй строки значение
в первой строке этих равенств соответствующим значением из второй строки значение ![]() - выражением из третьей, строки и т. д., получим разложение
- выражением из третьей, строки и т. д., получим разложение ![]() в цепную дробь:
в цепную дробь:
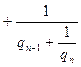
![]()
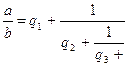
Выражения, получающиеся из цепной дроби при отбрасывании всех ее звеньев, начиная с некоторого звена, назовем подходящими дробями. Первая: подходящая дробь ![]() получится при отбрасывании всех звеньев, начиная с
получится при отбрасывании всех звеньев, начиная с ![]() :
: ![]() .
.
Вторая подходящая дробь ![]() получается отбрасыванием всех звеньев, начиная с
получается отбрасыванием всех звеньев, начиная с ![]() :
: ![]() . Точно так же
. Точно так же
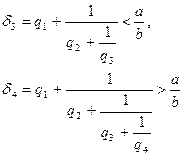
и т. д.
В силу способа образования подходящих дробей возникают очевидные неравенства:
![]() ;
; ![]() .
.
Запишем k-ю подходящую дробь ![]() в виде
в виде ![]()
![]() ,
,
и найдем закон образования числителей и знаменателей подходящих дробей, Преобразуем первые подходящие дроби ![]() ,
, ![]() ,
, ![]() :
:
![]() ;
; ![]() ,
, ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
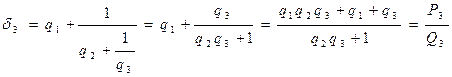 ;
;
![]() ;
; ![]()
Отсюда получаем:
![]() ;
; ![]() .
.
Применяя индукцию, докажем, что соотношения того же вида
![]() ,
, ![]() (7).
(7).
выполняются для всех ![]() .
.
Действительно, пусть равенства (7) выполняются для некоторого ![]() . Из определения подходящих дробей непосредственно следует, что при замене в выражении
. Из определения подходящих дробей непосредственно следует, что при замене в выражении ![]() величины
величины ![]() на
на ![]() перейдет в
перейдет в ![]() . Согласно индукционному предположению
. Согласно индукционному предположению
![]() .
.
Заменяя здесь ![]() на
на ![]() , получим:
, получим:
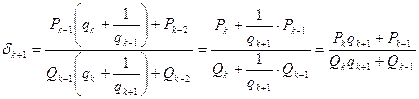 .
.
Отсюда, так как ![]() , следует, что
, следует, что
![]() ,
, ![]() .
.
Таким образом, из выполнения равенств (7) для некоторого ![]() следует выполнение их для
следует выполнение их для ![]() Но для
Но для ![]() равенства (7) - выполняется и, следовательно, их справедливость установлена для всех
равенства (7) - выполняется и, следовательно, их справедливость установлена для всех ![]() .
.
Покажем теперь, что разность соседних подходящих дробей ![]() удовлетворяет соотношению
удовлетворяет соотношению
![]()
![]() .
(8)
.
(8)
Действительно,
![]() .
.
Пользуясь формулами (7), преобразуем числитель полученной дроби:
![]() .
.
Выражение, стоящее в скобках, получается из исходного заменой ![]() на
на ![]() . Повторяя такие же преобразования для получающихся выражений, получим, очевидно, цепь равенств:
. Повторяя такие же преобразования для получающихся выражений, получим, очевидно, цепь равенств:
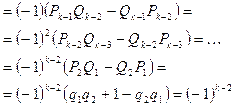
![]()
![]()
Отсюда следует, что
Если разложение ![]() в цепную дробь имеет
в цепную дробь имеет ![]() звеньев, то п-я подходящая дробь
звеньев, то п-я подходящая дробь ![]() совпадает с
совпадает с ![]() . Применяя равенство (8), при
. Применяя равенство (8), при ![]() получим
получим
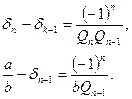 (9)
(9)
Вернемся теперь к решению уравнения
![]() ,
, ![]() (10)
(10)
Перепишем соотношение (9) в виде ![]() .
.
Приводя к общему знаменателю и отбрасывая его, получим
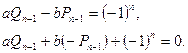
Умножим это соотношение на ![]() . Тогда
. Тогда
![]()
Отсюда следует, что пара чисел ![]() ,
,
![]() ,
, ![]() , (11)
, (11)
является решением уравнения (10) и согласно теореме все решения этого уравнения имеют вид
![]() ,
, ![]()
![]()
Полученный результат полностью решает вопрос о нахождении всех целочисленных решений уравнения первой степени с двумя неизвестными. Перейдем теперь к рассмотрению некоторых уравнений второй степени.
Похожие работы
... в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, • в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. . Как составлял и решал Диофант квадратные уравнения , В “Арифметике” Диофанта нет систематического изложения алгебры, однако в ней содержится ...
дробно рассмотрено преобразование групп общих решений тригонометрических уравнений. В третьем разделе рассматриваются нестандартные тригонометрические уравнения, решения которых основано на функциональном подходе. В четвертом разделе рассматриваются тригонометрические неравенства. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и ...
... ; , т.е. . ; Получили общее решение: , где . Способ 2. Рассмотрим еще один способ нахождения решения ЛДУ с двумя неизвестными, а для этого рассмотрим уравнение вида . Уравнения такого вида называются линейными однородными диофантовыми уравнениями (ЛОДУ). Выражая неизвестную , через неизвестную приходим к . Так как x должен быть целым числом, то, где - произвольное целое число. Значит. ...
... если точка начального приближения далека от точки решения, то метод Ньютона - Рафсона может не сходиться совсем. Геометрическая интерпретация не сходящегося метода Ньютона - Рафсона приведена на рис. 1б. Алгоритм Назначение: поиск решения уравнения (1) Вход: Начальное приближение x0 Точность (число итераций I) Выход: xI - решение уравнения (1) Инициализация: calculate f’(x0) Шаги ...
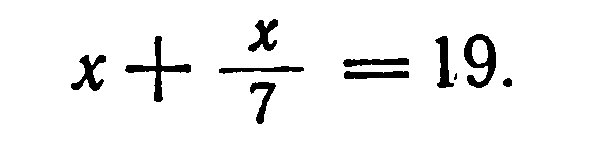
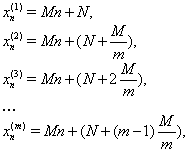

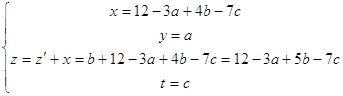
0 комментариев