Навигация
ПРИМЕРЫ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ С ТРЕМЯ НЕИЗВЕСТНЫМИ
3. ПРИМЕРЫ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ С ТРЕМЯ НЕИЗВЕСТНЫМИ
П р и м е р I. Рассмотрим уравнение второй степени с тремя неизвестными:
![]() (12)
(12)
Геометрически решение этого уравнения в целых числах можно истолковать как нахождение всех пифагоровых треугольников, т. е. прямоугольных треугольников, у которых и катеты ![]() ,
, ![]() и гипотенуза
и гипотенуза ![]() выражаются целыми числами.
выражаются целыми числами.
Обозначим через ![]() общий наибольший делитель чисел
общий наибольший делитель чисел ![]() и
и ![]() :
: ![]() . Тогда
. Тогда
![]() ,
, ![]() ,
,
и уравнение (12) примет вид
![]() .
.
Отсюда следует, что ![]() делится на
делится на ![]() и, значит,
и, значит, ![]() кратно
кратно ![]() :
: ![]() .
.
Теперь уравнение (12) можно записать в виде
![]() ;
;
сокращая на ![]() , получим
, получим
![]() .
.
Мы пришли к уравнению того же вида, что и исходное, причем теперь величины ![]() и
и ![]() не имеют общих делителей, кроме 1. Таким образом, при решении уравнения (12) можно ограничиться случаем, когда
не имеют общих делителей, кроме 1. Таким образом, при решении уравнения (12) можно ограничиться случаем, когда ![]() и
и ![]() взаимно просты. Итак, пусть
взаимно просты. Итак, пусть ![]() . Тогда хотя бы одна из величин
. Тогда хотя бы одна из величин ![]() и
и ![]() (например,
(например, ![]() ) будет нечетной. Перенося
) будет нечетной. Перенося ![]() в правую часть уравнения (12), получим
в правую часть уравнения (12), получим
![]() ;
; ![]() . (13)
. (13)
Обозначим через ![]() общий наибольший делитель выражений
общий наибольший делитель выражений ![]() и
и ![]() . Тогда
. Тогда
![]() ,
, ![]() , (14)
, (14)
где ![]() и
и ![]() взаимно просты.
взаимно просты.
Подставляя в (13) значения ![]() и
и ![]() , получим
, получим
![]() .
.
Так как числа ![]() и
и ![]() не имеют общих делителей, то полученное равенство возможно только в том случае, когда
не имеют общих делителей, то полученное равенство возможно только в том случае, когда ![]() и
и ![]() будут полными квадратами:
будут полными квадратами:
![]() ,
, ![]() .
.
Но тогда
![]()
и
![]() (15)
(15)
Найдем теперь ![]() и
и ![]() из равенств (14). Сложение этих равенств дает:
из равенств (14). Сложение этих равенств дает:
![]() ;
; ![]() . (16)
. (16)
Вычитая второе из равенств (14) из первого, получим
![]() ;
; ![]() (17)
(17)
В силу нечетности ![]() из (15) получаем, что
из (15) получаем, что ![]() ,
, ![]() и
и ![]() также нечетны. Более того,
также нечетны. Более того, ![]() , так как иначе из равенств
, так как иначе из равенств
![]() и
и ![]()
следовало бы, что величины ![]() и
и ![]() имеют общий делитель
имеют общий делитель ![]() , что противоречит предположению об их взаимной простоте. Числа
, что противоречит предположению об их взаимной простоте. Числа ![]() и
и ![]() связаны с взаимно простыми числами
связаны с взаимно простыми числами ![]() и
и ![]() равенствами
равенствами
![]() ,
, ![]()
и в силу этого сами взаимно просты; ![]() , так как
, так как ![]() , что ясно из равенств (14).
, что ясно из равенств (14).
Подставляя в равенства (15) - (17) ![]() , получим формулы:
, получим формулы:
![]() ,
, ![]() ,
, ![]() , (18)
, (18)
дающие при нечетных взаимно простых ![]() и
и ![]()
![]() все свободные от общих делителей тройки целых положительных чисел
все свободные от общих делителей тройки целых положительных чисел ![]() ,
, ![]() ,
, ![]() , удовлетворяющие уравнению (12). Простой подстановкой
, удовлетворяющие уравнению (12). Простой подстановкой ![]() ,
, ![]() и
и ![]() в уравнение (12) легко проверить, что при любых
в уравнение (12) легко проверить, что при любых ![]() и
и ![]() числа (18) удовлетворяют этому уравнению.
числа (18) удовлетворяют этому уравнению.
Для начальных значений ![]() и
и ![]() формулы (18) приводят к следующим часто встречающимся равенствам:
формулы (18) приводят к следующим часто встречающимся равенствам:
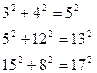
![]()
![]()
Как уже было сказано, формулы (18) дают только те решения уравнения
![]() ,
,
в которых числа ![]() ,
, ![]() и
и ![]() не имеют общих делителей. Все остальные целые положительные решения-этого уравнения получаются умножением решений, содержащихся в формулах (18), на произвольный общий множитель
не имеют общих делителей. Все остальные целые положительные решения-этого уравнения получаются умножением решений, содержащихся в формулах (18), на произвольный общий множитель ![]() .
.
Тем же путем, каким мы получили все решения уравнения (12), могут быть получены и все решения других уравнений того же типа.
П р и м е р II. Найдем все решения уравнения
![]() (19)
(19)
в целых положительных попарно взаимно простых числах ![]() ,
, ![]() ,
, ![]() .
.
Заметим, что если ![]() ,
, ![]() ,
, ![]() есть решение уравнения (19) и
есть решение уравнения (19) и ![]() ,
, ![]() ,
, ![]() не имеют общего делителя, отличного от 1, то они и попарно взаимно просты. Действительно, если
не имеют общего делителя, отличного от 1, то они и попарно взаимно просты. Действительно, если ![]() и
и ![]() кратны простому числу
кратны простому числу ![]() , то из равенства
, то из равенства
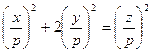
следует, так как его левая часть - целое число, что ![]() кратно
кратно ![]() . То же самое будет, если
. То же самое будет, если ![]() и
и ![]() или
или ![]() и
и ![]() делятся на
делятся на ![]() .
.
Заметим, что ![]() должно быть числом нечетным для того, чтобы общий наибольший делитель
должно быть числом нечетным для того, чтобы общий наибольший делитель ![]() ,
, ![]() ,
, ![]() был равен 1. Действительно, если
был равен 1. Действительно, если ![]() четно, то левая часть уравнения (19) будет четным числом и, значит, z также будет четным. Но
четно, то левая часть уравнения (19) будет четным числом и, значит, z также будет четным. Но ![]() и
и ![]() будут тогда кратны 4. Отсюда следует, что
будут тогда кратны 4. Отсюда следует, что ![]() должно делиться на 4, другими словами, что
должно делиться на 4, другими словами, что ![]() тоже должно быть четным числом. Значит, если
тоже должно быть четным числом. Значит, если ![]() четно, то все числа
четно, то все числа ![]() ,
, ![]() ,
, ![]() должны быть четными. Итак, в решении без общего отличного от 1 делителя
должны быть четными. Итак, в решении без общего отличного от 1 делителя ![]() должно быть нечетным. Отсюда уже следует, что и
должно быть нечетным. Отсюда уже следует, что и ![]() должно быть тоже нечетным. Перенося
должно быть тоже нечетным. Перенося ![]() в правую часть, мы получаем:
в правую часть, мы получаем:
![]() .
.
Но ![]() и
и ![]() имеют общим наибольшим делителем 2. Действительно, пусть их общий наибольший делитель будет
имеют общим наибольшим делителем 2. Действительно, пусть их общий наибольший делитель будет ![]() . Тогда
. Тогда
![]() ,
, ![]() ,
,
где ![]() и
и ![]() - целые числа. Складывая и вычитая эти равенства, мы будем иметь:
- целые числа. Складывая и вычитая эти равенства, мы будем иметь:
![]() ,
,![]() .
.
Но ![]() и
и ![]() нечетны и взаимно просты. Поэтому общий наибольший делитель
нечетны и взаимно просты. Поэтому общий наибольший делитель ![]() и
и ![]() будет 2. Отсюда следует, что
будет 2. Отсюда следует, что ![]() .
.
Итак, или ![]() , или
, или ![]() нечетно. Поэтому или
нечетно. Поэтому или
числа
![]() и
и ![]()
взаимно просты, или взаимно просты числа
![]() и
и ![]() .
.
В первом случае из равенства
![]()
следует, что
![]() ,
, ![]() ,
,
а во втором случае из равенства
![]()
следует
![]() ,
, ![]() ,
,
где ![]() и
и ![]() целые,
целые, ![]() - нечетное число и
- нечетное число и ![]() ,
, ![]() . Решая эти две системы уравнений относительно
. Решая эти две системы уравнений относительно ![]() и
и ![]() и находя
и находя ![]() , мы получаем или
, мы получаем или
![]() ,
, ![]() ,
, ![]() или
или
![]() ,
, ![]() ,
, ![]() ,
,
где ![]() нечетно. Объединяя эти две формы представления решения
нечетно. Объединяя эти две формы представления решения ![]() ,
, ![]() ,
, ![]() мы получаем общую формулу
мы получаем общую формулу
![]() ,
, ![]() ,
, ![]() ,
,
где ![]() нечетно. Но для того чтобы
нечетно. Но для того чтобы ![]() и
и ![]() были целыми числами, необходимо, чтобы
были целыми числами, необходимо, чтобы ![]() было четным. Полагая
было четным. Полагая ![]() и
и ![]() , мы получим окончательно общие формулы, дающие все решения уравнения (19) в целых положительных без общего делителя, большего 1, числах
, мы получим окончательно общие формулы, дающие все решения уравнения (19) в целых положительных без общего делителя, большего 1, числах![]() ,
, ![]() ,
, ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
(19')
,
(19')
где ![]() и
и ![]() положительны, взаимно просты и
положительны, взаимно просты и ![]() нечетно. При этих условиях величины
нечетно. При этих условиях величины ![]() и
и ![]() выбираются произвольно, но так, чтобы
выбираются произвольно, но так, чтобы ![]() было положительно. Формулы (19') действительно дают все решения в целых положительных и взаимно простых числах
было положительно. Формулы (19') действительно дают все решения в целых положительных и взаимно простых числах ![]() ,
, ![]() ,
, ![]() , так как, с одной стороны, мы доказали, что
, так как, с одной стороны, мы доказали, что ![]() ,
, ![]() ,
, ![]() в этом случае должны представляться по формулам (19'), а с другой стороны, если мы зададим числа
в этом случае должны представляться по формулам (19'), а с другой стороны, если мы зададим числа ![]() и
и ![]() , удовлетворяющие нашим условиям, то
, удовлетворяющие нашим условиям, то ![]() ,
, ![]() ,
, ![]() будут действительно взаимно просты и будут решением уравнения (19).
будут действительно взаимно просты и будут решением уравнения (19).
Похожие работы
... в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, • в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. . Как составлял и решал Диофант квадратные уравнения , В “Арифметике” Диофанта нет систематического изложения алгебры, однако в ней содержится ...
дробно рассмотрено преобразование групп общих решений тригонометрических уравнений. В третьем разделе рассматриваются нестандартные тригонометрические уравнения, решения которых основано на функциональном подходе. В четвертом разделе рассматриваются тригонометрические неравенства. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и ...
... ; , т.е. . ; Получили общее решение: , где . Способ 2. Рассмотрим еще один способ нахождения решения ЛДУ с двумя неизвестными, а для этого рассмотрим уравнение вида . Уравнения такого вида называются линейными однородными диофантовыми уравнениями (ЛОДУ). Выражая неизвестную , через неизвестную приходим к . Так как x должен быть целым числом, то, где - произвольное целое число. Значит. ...
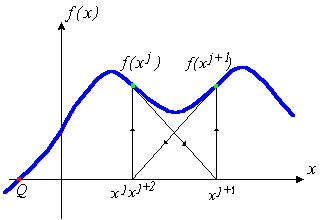
... если точка начального приближения далека от точки решения, то метод Ньютона - Рафсона может не сходиться совсем. Геометрическая интерпретация не сходящегося метода Ньютона - Рафсона приведена на рис. 1б. Алгоритм Назначение: поиск решения уравнения (1) Вход: Начальное приближение x0 Точность (число итераций I) Выход: xI - решение уравнения (1) Инициализация: calculate f’(x0) Шаги ...

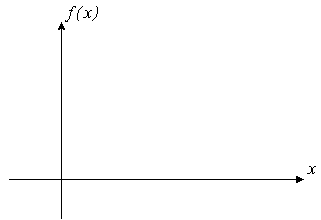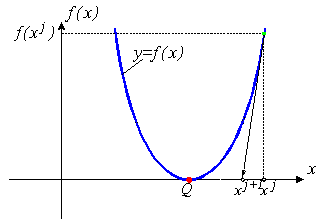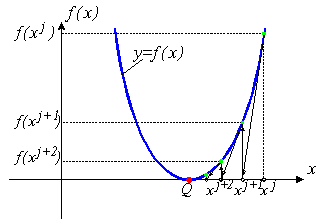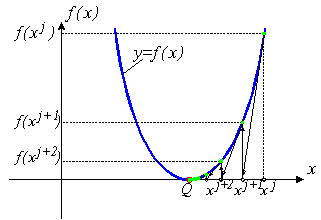
0 комментариев