По следующим данным распределения рабочих цеха по проценту выполнения месячного задания определить моду и медиану

2. По следующим данным распределения рабочих цеха по проценту выполнения месячного задания определить моду и медиану.

Таблица 5.2

Данные о выполнении производственного задания

Выполнение месячного задания, процент	Число рабочих, чел.	Накопленные частоты от начала ряд
95-100	3	3
100-105	20	23
105-110	10	33
110-115	5	38
115-120	4	42
Итого	42	–

Модой в статистике называют наиболее часто встречающееся в исследуемой совокупности значение признака. Следовательно, в данной задаче модальным будет интервал от 100 до 105 процентов, так как на него приходится наибольшее число рабочих (20 чел.).

Моду определяют по формуле:

Mo = x₀ + ∙ (x₁ – x₀),

где x₀ и x₁ - соответственно нижняя и верхняя границы модального интервала;

m₂ - частота модального интервала;

m₁ и m₃ - частоты интервала, соответственно, предыдущего и следующего за модальным.

Подставим значения в формулу:

Mo = 100 + ´ (105 – 100) = 103,1%.

Иначе говоря, наибольшее число рабочих выполняют месячное задание на 103,1%.

Медианой в статистике называют срединное значение признака в исследуемой совокупности. Следовательно, медианным является интервал, на который приходится 50% накопленных частот данного ряда, что по условию задачи 42 : 2 = 21.

В нашей задаче медиана находится в интервале от 100 до 105% , так как на данный интервал приходится накопленная частота 23.

Медиану определяют по формуле:

Me = x₀ + ∙ (x₁ – x₀),

где x₀ и x₁ - соответственно нижняя и верхняя границы медианного интервала;

N - сумма частот ряда;

N₀ - сумма частот, накопившаяся до начала медианного интервала;

N₁ - частота медианного интервала.

Подставим соответствующее значение в формулу:

Me = 100 +  ´ 5 = 104,5%.

Таким образом, 50% всех рабочих выполняют производственное задание менее чем на 104,5%; 50% - более чем на 104,5%.

Тема 6. Ряды динамики

Рядами динамики называют ряды, которые характеризуют изменение явления во времени. Ряды динамики бывают моментные и интервальные. Моментные ряды характеризуют изменение явления в динамике на определенный момент времени (чаще - на начало или конец периода). Интервальные ряды характеризуют изменение явления в динамике за определенный период времени (месяц, квартал, год).

В экономическом анализе используют аналитические показатели динамики. К ним относят абсолютный прирост, средний абсолютный прирост, темп роста, темп прироста, средний темп роста, абсолютное значение одного процента прироста. Данные показатели широко используются в статистической практике, что вызывает необходимость тщательного изучения порядка их расчета.

Рассмотрим на примере расчет аналитических показателей ряда динамики (табл. 6.1).

Таблица 6.1

Данные о производстве в цехе

Месяц	Выпуск цехом товарной продукции, тыс. руб.	Показатели динамики
		Абсо­лютный прирост (D), тыс. руб.	Темп роста (Тр)		Темп прироста (Тпр)		Абсолютное значение 1% прироста (А), тыс. руб.
			Цепной	Базис­ный	Цепной	Базис­ный
1	236	–	–	100,0	–	–	–
2	244	8	103,4	103,4	3,4	3,4	2,4
3	246	2	100,8	104,2	0,8	4,2	2,5
4	249	3	101,2	105,5	1.2	5,5	2,5
5	250	1	100,4	105,9	0,4	5,9	2,5
6	252	2	100,8	106,8	0,8	6,8	2,5

Абсолютный прирост (D) определяется как разность между отчетным и предыдущим уровнями ряда динамики, т.е. по формуле:

D = y_i – y_i–1,

где y_i, y_i–1 - уровни ряда динамики.

Так, например, абсолютный прирост продукции цеха в феврале по сравнению c январем составил: 244 – 236 = 8 тыс. руб., а в марте по сравнению с февралем: 246 – 244 = 2 тыс. руб. и т.д.

Средний абсолютный прирост () определяется на основе данных абсолютных приростов по следующей формуле:

 или ,

где n - число уровней ряда динамики;

y₁ и y_n - соответственно первый и последний уровни ряда динамики.

Темп роста (Т_р) определяется по формуле:

Т_р =  ´ 100%,

где y₀ - уровень ряда динамики, взятый за базу сравнения.

Темп роста рассчитывается по принципу цепных и базисных соотношений. В том числе, когда за базу сравнения принимается предыдущий период - это цепные показатели темпа роста, когда сравнение осуществляется с любым другим уровнем ряда динамики, взятым за базу сравнения - базисные темпы роста.

Так, в феврале по сравнению с январем выпуск продукции в цехе составил: Т_р2 = (244 : 236) ´ 100% = 103,4%, а в марте по сравнению с февралем: Т_р3 = (246 : 244) ´ 100% = 100,8% и т.д.

Если за базу сравнения взять январь, то выпуск продукции в цехе в марте по сравнению с январем составил: (246 : 236) ´ 100% = 104,2%, а в апреле по сравнению с январем: (249 : 236) ´ 100% = 105,5% и т.д.

Темп прироста (Т_пр) в отличие от темпа роста характеризует относительный прирост явления в отчетном периоде по сравнению с тем уровнем, с которым осуществляется сравнение и определяется:

Т_пр = Т_р – 100.

Так, в марте объем продукции цеха по сравнению с февралем увеличился на 0,8% (100,8 – 100), а по сражению с январем - на 4,2% (104,2 – 100) и т.д.

Абсолютное значение одного процента прироста (А) характеризует абсолютный эквивалент одного процента прироста и определяется по формуле:

А = .

Так, в марте абсолютное значение одного процента прироста составило: (2 : 0,8) = 2,4 млн. руб. и т.д.

Средний темп роста () за период динамики определяют по формуле средней геометрической двояким способом - на основе данных цепных коэффициентов динамики, либо на основе данных абсолютных уровней ряда динамики по формуле:

∙100

или

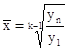∙100,

где x₁, x₂, …, x_n - коэффициенты динамики по отношению к предыдущему периоду;

n - число коэффициентов динамики;

k - число абсолютных уровней ряда динамики.

Так, за первое полугодие средний годовой темп роста продукции в цехе составил:  =  =  = 1,014 ´ 100 = 101,4% или  =  =  = 1,014 ´ 100 = 101,4%.

Один из важнейших вопросов, возникающих при изучении рядов динамики - это выявление тенденции развития экономической закономерности в динамике. Для этой цели применяются разнообразные статистические методы, в частности, метод укрупнения интервалов, метод скользящей средней, метод аналитического выравнивания.

Наиболее простым в использовании является метод укрупнения интервалов, основанный на укрупнении периодов времени, к которым относятся уровни ряда. Выявление тенденции осуществляется по новому укрупненному ряду динамики.

Другой метод - метод скользящей средней заключается в замене первоначальных уровней ряда динамики средними арифметическими, найденными по способу скольжения, начиная с первого уровня ряда с постепенным включением последующих уровней.

Наиболее совершенным методом выявления тенденции ряда динамики является метод аналитического выравнивания, который заключается в замене первоначальных уровней ряда новыми, найденными во времени "t" построением аналитического уравнения связи.

Рассмотрим на примере возможности применения каждого из методов выравнивания при выявлении тенденции ряда динамики.

Известны следующие данные выполнения программы участком "молдинги" цеха ЗИЛ-130 прессового корпуса за 1989 г. (табл.6.2).

Таблица 6.2

Месяц	Выполнение программы, млн. руб.	t	t2	ty	= 18,6 + 0,09t
I	18,6	-6	36	-111,6	18,1
II	17,3	-5	25	-86,5	18,2
III	18,9	-4	16	-75,6	18,3
IV	18,2	-3	9	-54,6	18,3
V	17,9	-2	4	-35,8	18,4
VI	19,1	-1	1	-19,1	18,5
VII	19,6	1	1	19,6	19,2
VIII	17,5	2	4	35,0	19,1
IX	19,2	3	9	57,6	19,0
X	19,8	4	16	79,2	18,9
XI	18,3	5	25	91,5	18,8
XII	19,4	6	36	116,4	18,7
Итого:	223,8	0	182	16,1	223,5

1. По методу укрупнения интервалов имеем новые укрупненные поквартально уровни ряда динамики:

у₁ = 18,6 + 17,3 + 18,9 = 54,8;

y₂ = 18,2 + 17,9 + 19,1 = 55,2 и т.д.

Выровненный ряд динамики примет вид: 54,8 55,2 56,3 57,5.

То есть наблюдается четно выраженная тенденция увеличения выпуска молдингов цехом за 1989 г.

2. Употребляя те же данные, применим метод скользящей средней, используя семичленную скользящую среднюю. Тогда:

 =  = 18,5;

 =  = 18,4 и т.д.

Выравненный с помощью семичленной скользящей средней ряд динамики примет вид: 18,5 18,4 18,6 18,7 18,8 19,0.

Таким образом, подтверждается тенденция увеличения выпуска молдингов в течение 1989 г.

3. Используя метод отсчета от условного нуля введем условное обозначение времени "t", придав ему определенные значения так, чтобы ∑t = 0 (см. табл. 6.2).

Судя по выявленной с помощью двух предыдущих методов тенденции выпуска молдингов в течение года, можно сказать, что наиболее вероятна линейная зависимость данного распределения от времени "t" и данному распределению соответствует уравнение прямой  = a₀ + a₁t.

Для нахождения параметров a₀ и a₁ используем систему уравнений

 ,

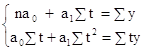так как ∑t = 0, о имеем

a₀ =  =  = 18,6;

a₁ =  =  = 0,09.

Следовательно, уравнение прямой примет вид:

 = 18,6 + 0,09t и будет в данном случае искомым, так как ∑y = ∑.

Тема 7. Показатели вариации

Наряду со средней величиной, характеризующей типичный уровень варьирующего признака, около которого колеблются отдельные значения признака, рассматривают показатели вариации (колеблемости) признака, позволяющие количественно измерить величину этой колеблемости.

К показателям вариации относят: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Простейшим показателем вариации является размах вариации, который рассчитывается по следующей формуле:

R = Xmax – Xmin,

где Xmax, Xmin - соответственно, максимальное и минимальное значения признака в исследуемой совокупности.

Размах вариации характеризует диапазон колебаний признака в изучаемой совокупности и измеряется в тех же единицах, в которых выражен признак.

Рассчитывают среднее линейное отклонение, которое бывает невзвешенное и взвешенное. Если каждое значение признака встречается в совокупности один раз, то применяется формула среднего линейного отклонения невзвешенного:

,

где x - значение признака;

n - количество вариант.

Если имеется некоторая повторяемость значений признака, то применяется формула среднего линейного отклонения взвешенного:

,

где m - частота.

Среднее линейное отклонение характеризует абсолютный размер колеблемости признака около средней и измеряется в тех же единицах, в которых выражен признак.

Наиболее точным показателем вариации является среднее квадратическое отклонение. Для его определения предварительно рассчитывают показатель дисперсии. Дисперсия невзвешенная определяется по формуле:

σ² =.

Дисперсия взвешенная определяется по формуле:

σ² =.

Тогда, соответственно, для расчета среднего квадратического отклонения невзвешенного используют формулу:

σ =,

а для расчета среднего квадратического отклонения взвешенного - следующую формулу:

σ =.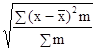

Как и среднее линейное отклонение, среднее квадратическое отклонение характеризует абсолютный размер колеблемости признака около средней, однако является более точной характеристикой.

В отличие от среднего линейного и среднего квадратического отклонения коэффициент вариации является мерой относительной колеблемости признака около средней и характеризует степень однородности признака в изучаемой совокупности. Он определяется по формуле:

υ_σ =  ´ 100%.

Если исследуемую совокупность единиц расчленить на группы, то вправе считать, что общая дисперсия всей совокупности варьирует (изменяется) под влиянием дисперсий для каждой отдельной группы, так называемых групповых или частных дисперсий и межгрупповой дисперсии. Эти дисперсии связаны между собой правилом сложения дисперсий. При использовании правила сложения дисперсий в экономическом анализе по величине частной дисперсии может решаться задача выявления наиболее эффективной в производстве системы (формы, структуры и т.п.) организации труда, его оплаты и т.п.

Частные или групповые дисперсии характеризуют колеблемость изучаемого признака в каждой отдельной группе и определяются по следующей формуле:

и их средняя величина

,

где i = 1, 2, …, n - номер группы;

m_i - численность единиц в группе.

Межгрупповая дисперсия характеризует колеблемость частных средних около общей средней  и определяется следующим образом:

γ² =.

При соблюдении правила сложения дисперсий должно соблюдаться равенство:

σ² = + γ².

Проиллюстрируем расчет показателей вариации по данным о распределении рабочих по стажу работы (табл. 7.1).