R = Xmax – Xmin = 14 – 10 = 4 года, т.е. диапазон колебания стажа рабочих в исследуемой совокупности составляет 4 года

1. R = Xmax – Xmin = 14 – 10 = 4 года, т.е. диапазон колебания стажа рабочих в исследуемой совокупности составляет 4 года.

2.  =  = 11,4 года

 =  = 1,1 года.

Таблице 7.1

Стаж работы рабочих

Стаж работы рабочего, лет (x)	Число рабочих, чел. (m)	x∙m	x –	| x –|m	(x –)2	(x –)2m
10	14	140	-1,4	19,6	1,96	27,44
11	11	121	-0,4	4,4	0,16	1,76
12	8	96	0,6	4,8	0,36	2,88
13	6	78	1,6	9,6	2,56	15,36
14	4	56	2,6	10,4	6,76	24,04
Итого	43	491	–	48,8	11,80	74,48

В среднем на 1,1 года отклоняется стаж отдельных рабочих от среднего стажа по совокупности.

3. σ² = =  = 1,73;

σ =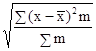=  = 1,3 года.

Величина σ = 1,3 года характеризует колеблемость стажа работы рабочих в данной совокупности:

υ_σ =  ´ 100 =  ´ 100 = 11,4%.

Таким образом, на 11,4% варьирует состав рабочих по стажу работы в исследуемой совокупности.

Тема 8. Индексы

В статистике индексами называют относительные величины, показывающие соотношение показателей во времени, пространстве, а также фактических показателей с плановыми.

Индексы измеряются в процентах.

Для некоторых простых, единичных явлений, которые допускают непосредственное сравнение, строят индивидуальные индексы. Дня явлений сложных, состоящих из непосредственно несоизмеримых элементов, строят сводные индексы. Так, для характеристики динамики производства конкретного вида продукции, применяется индивидуальный индекс. Если же исследователя интересует динамика выпуска всей продукции предприятия, то в этом случае строится сводный индекс, так как отдельные виды продукции предприятия непосредственно несоизмеримы.

Разработанная статистикой теория индексов позволяет решить следующие задачи:

1) определять соотношение показателей во времени, пространстве, фактических данных с плановыми;

2) выявлять абсолютные результаты измерения показателей в аналогичных направлениях;

3) определять относительное и абсолютное влияние отдельных факторов на такое изменение при условии, что факторы представлены в виде произведения.

В теории индексов наиболее часто используются следующие обозначения: I - индивидуальный индекс; J - сводный индекс.

Порядок построения индивидуальных индексов весьма прост: в числителе дроби записывается показатель на уровне отчетного периода, в знаменателе - на уровне базисного периода. Например:

I_p = ; I_t = ; I_q =  и т.д.,

где I_p - индивидуальный индекс цен;

I_t - индивидуальный индекс трудоемкости;

I_q - индивидуальный индекс продукции;

p₁ и p₀ - цена единицы продукции, соответственно, в отчетном и базисном периодах, руб.;

t₁ и t₀ - трудоемкость изготовления единицы продукции, соответственно, в отчетном и базисном периодах, ч;

q₁ и q₀ - количество произведенной продукции, соответственно, в отчетном и базисном периодах, шт.

Существуют цепные и базисные индивидуальные индексы. В цепных индексах каждый последующий период сравнивается с предыдущим, например:

; ;  и т.д.

Нетрудно заметить, что перемножение цепных индексов дает в итоге сравнение явлений, разделенных рядом промежутков времени (базисные индексы):

 =  ´  ´ .

Естественно, если в задаче известен базисный индекс и какие-то из цепных, то для нахождения других цепных индексов необходимо производить деление.

Следует знать, что индексы динамики, планового задания и выполнения плана связаны между собой известным из теории относительных величин соотношением:

Iдинамики = Iпл. задания ´ Iвыполнения плана.

Если в задаче требуется найти абсолютное изменение какого-то явления, то оно определяется как разница между числителем и знаменателем индекса:

(p₁ – p₀); (t₁ – t₀) и т.д.

Если при этом ставится задача определить, как влияет это изменение на какое-то многофакторное явление, то найденная разность между числителем и знаменателем качественного индекса (цен, трудоемкости и т.п.) умножается на соответствующий количественный фактор (количество продукции, численность работающих и т.п.) на уровне отчетного периода. Разность между числителем и знаменателем количественного индекса (продукции, численности работающих и т.п.) умножается на соответствующий качественный фактор (трудоемкость и т.п.) на уровне базисного периода:

(p₁ – p₀)q₁ - размер экономии (перерасхода) денежных средств от снижения (повышения) цен;

(t₁ – t₀)q₁ - размер увеличения (уменьшения) затрат труда на производство продукции от повышения (снижения) трудоемкости;

(q₁ – q₀)p₀ - размер экономии (перерасхода) денежных средств от изменения объема выпуска продукции;

(q₁ – q₀)t₀ - размер увеличения (уменьшения) затрат труда на производство продукции от изменения объема выпуска продукции и т.д.

В отличие от индивидуальных индексов, сводные индексы представляют собой результат сравнения сложных явлений, состоящих из непосредственно несоизмеримых элементов.

Сводные индексы представляют собой соотношение сумм произведений индексируемых величин и их соизмерителей. В качестве соизмерителей могут выступать: трудоемкость изготовления продукции (t), цена единицы продукции (p), себестоимость единицы продукции (z). Название сводного индекса определяется изменяющимся (индексируемым) показателем. Индексируемый показатель записывают в числителе на уровне отчетного периода, в знаменателе - на уровне базисного периода или на уровне планового задания. Если индексируется качественный показатель (цена, трудоемкость, себестоимость), то соответствующий ему количественный соизмеритель фиксируется на уровне отчетного периода. Если индексируется количественный показатель, то соответствующий ему качественный соизмеритель фиксируется на уровне базисного периода или на уровне планового задания. Исходя из этого, сводный индекс цен запишется:

J_p =;

сводный индекс трудоемкости: J_t =;

сводный индекс себестоимости: J_z =;

сводный индекс физического объема продукции:

J_q = (при наличии соизмерителя p);

J_q = (при наличии соизмерителя t);

J_q = (при наличии соизмерителя z).

Индексы цен, трудоемкости и себестоимости продукции относятся к индексам постоянного состава, так как q = const. Индексы физического объема продукции независимо от соизмерителя относятся к индексам структурных сдвигов, так как учитывается изменение в ассортименте и объеме продукции. В том случае, когда в сводном индексе индексируется сам показатель и его соизмеритель, оба составляющих в числителе записываются на уровне отчетного периода, в знаменателе - на уровне базисного периода, а название сводного индекса определяется индексируемыми составляющими. Так, сводный индекс объема продукции в стоимостном выражении запишется J_qp =; индекс затрат труда на производство продукции J_qt =; индекс денежных затрат на производство продукции J_qz =.

Такие индексы относятся к индексам переменного состава, так как варьируют оба составляющих.

В статистическом анализе используется взаимосвязь индексов переменного состава и структурных сдвигов, которая проявляется в виде двух свойств индексов.

Первое свойство индексов: индекс переменного состава равен произведению индексов постоянного состава и структурных сдвигов:

J_qp = J_q ∙ J_p;  = ;

J_qt = J_q ∙ J_t;  = ;

J_qz = J_q ∙ J_z;  = .

Второе свойство индексов: разность числителя и знаменателя индекса переменного состава равна сумме разностей числителя и знаменателя индексов постоянного состава и структурных сдвигов:

Dqp_(qp) = Dqp_(q) + Dqp_(p); ∑q₁p₁ – ∑q₀p₀ = (∑q₁p₀ – ∑q₀p₀) + (∑q₁p₁ – ∑q₁p₀);

Dqt_(qt) = Dqt_(q) + Dqt_(t); ∑q₁t₁ – ∑q₀t₀ = (∑q₁t₀ – ∑q₀t₀) + (∑q₁t₁ – ∑q₁t₀);

Dqz_(qz) = Dqz_(q) + Dqz_(z); ∑q₁z₁ – ∑q₀z₀ = (∑q₁z₀ – ∑q₀z₀) + (∑q₁z₁ – ∑q₁z₀).

Рассмотрим пример:

По одному из подразделений промышленного предприятия известны следующие данные (табл. 8.1).

Таблица 8.1

Вид продукции	Количество произведенной продукции, тыс. шт.		Цена 1 шт., руб.
	Базисный период	Отчетный период	Базисный период	Отчетный период
А	15	20	0,8	0,7
Б	1,5	2	2,0	1,5
В	5	10	1,0	0,8

Рассчитаем индивидуальные индексы продукции и индивидуальные индексы цен.

Индивидуальные индексы по соответствующим видам продукции составят:

I_q(А) =  =  ´ 100 = 133,3%;

I_q(Б) =  =  ´ 100 = 133,3%;

I_q(В) =  =  ´ 100 = 200%.

То есть в отчетном периоде по сравнению с базисным произведено продукции вида "А" и "Б", соответственно, на 33,3% больше, а вида "В" - на 100% больше.

Индивидуальные индексы цен по соответствующим видам продукции составят:

I_p(А) =  =  ´ 100 = 87,5%;

I_p(Б) =  =  ´ 100 = 75,0%;

I_p(В) =  =  ´ 100 = 80,0%.

То есть цена единицы продукции вида "А" в отчетном периоде по сравнению с базисным снизилась на 12,5% (100 – 87,5), вида "Б" - на 25% (100 – 75) и вида "В" - на 20% (100 – 80).

Индивидуальные индексы конкретного вида продукции в стоимостном выражении, соответственно, составят:

I_p(А) =  =  ´ 100 =  ´ 100 = 116,7%;

I_p(Б) =  =  ´ 100 =  ´ 100 = 100%;

I_p(В) =  =  ´ 100 =  ´ 100 = 160%.

Таким образом, объем продукции в стоимостном выражении вида "А" в отчетном периоде по сравнению с базисным увеличится на 16,7% (116,7 – 100), вида "В" - на 60% (160 – 100) и вида "Б" - останется без изменения (100 – 100).

Для того, чтобы ответить на вопрос, как уменьшился объем всей продукции предприятия в отчетном периоде по сравнению с базисным, необходимо рассчитать сводные индексы продукции, цен и физического объема продукции.

Сводный индекс объема продукции в стоимостном выражении составит:

J_qp =  =  ´ 100 =  ´ 100 = 125%;

Сводный индекс цен составит:

J_p =  =  ´ 100 =  ´ 100 = 83,3%;

Сводный индекс физического объема продукции составит:

J_q =  =  ´ 100 =  ´ 100 = 150%.

Используя первое свойство индексов, имеем:

J_qp = J_q ∙ J_p; 125% = 1,5 ´ 0,833 ´ 100%.

Используя второе свойство индексов, имеем:

Dqp_(qp) = Dqp_(q) + Dqp_(p), т.е. (25 – 20) = (30 – 20) + (25 – 30) или (+5) = (+10) + (-5).

Таким образом, можно сделать вывод: объём продукции в стоимостном выражении увеличился в целом на 25%, или на 5´(25 – 20) тыс. руб., в том числе за счет снижения цен на 16,7% (83,3 – 100) объем снизился на 5 тыс. руб. (25 – 30), а за счет увеличения физического объема продукции на 50% (150 – 100) объем продукции в стоимостном выражении увеличился на 10 тыс. руб.

Тема 9. Взаимосвязи явлений

Первый этап изучения связи явлений - выделение основных причинно-следственных связей и отделение их от второстепенных. Второй этап - построение модели. Последний этап - интерпретация результатов.

Признаки-аргументы называются факторами, а признаки-функции - результатами (результативными признаками).

Связи между явлениями делят по степени тесноты связи (полная или функциональная связь, неполная или статистическая связь), по направлению (прямая, обратная), по аналитическому выражению (линейная, нелинейная).

Для выявления связи, ее характера, направления используют методы приведения параллельных данных, балансовый, аналитических группировок, графический. Суть метода приведения параллельных данных: приводят два ряда данных о двух признаках, связь между которыми хотят выявить, и по характеру изменений делают заключение о наличии связи. Балансовый метод заключается в построении балансов - таблиц, где итог одной части равен итогу другой.

Методы аналитических группировок и графический изложены в соответствующих темах.

Удобная форма изложения данных - корреляционная таблица (табл. 9.1).

Таблица 9.1

Корреляционная таблица

Часовая выработка ткани, м	Количество станков, обслуживаемых одной работницей, шт.
	5-7	7-9	9-11	11-13	13-15	15-17	17-19	Итого
10 - 15	7	4		2	1			14
15 - 20	3	8	5	4				20
20 - 25		2	11	8		2		23
25 - 30			5	13	7	1		26
30 - 35				1	16	3		20
35 - 40				2	6	19	3	30
40 - 45					3	7	18	28
Итого:	10	14	21	30	33	32	21	161

Таблица показывает, что частоты концентрируются у диагонали, идущей из левого верхнего угла в правый нижний. Это указывает на то, что связь между количеством обслуживаемых работницей станков и ее часовой выработкой ткани прямая (с увеличением числа обслуживаемых станков увеличивается выработка) или близкая к прямой (концентрация частот идет почти по прямой линии).

По данным таблицы можно рассчитать среднюю выработку по каждой из семи групп работниц, выделенных по числу обслуживаемых станков. Обозначив эти средние значения через  и произведя расчеты, получаем:  = 14,0;  = 16,79;  = 22,51;  = 24,67;  = 32,65;  = 36,88;  = 41,79.

Данные таблицы и результаты расчетов можно изобразить графически с помощью поля корреляции. Ломаная линия на графике (линия значений ) называется эмпирической линией регрессии.

Показатели тесноты связи. Для оценки тесноты связи применяется ряд показателей, одни из которых называются эмпирическими или непараметрическими, другие (выводимые строго математически) - теоретическими.

Коэффициент знаков (коэффициент Фехнера) вычисляется на основании определения знаков отклонений вариантов двух взаимосвязанных признаков от их средних величин.

Если число совпадений знаков обозначать через a, число несовпадений - через b, а сам коэффициент - через i , то можно записать формулу этого коэффициента так:

.

Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается не по значениям двух взаимосвязанных признаков, а по их рангам следующим образом:

ρ_x/y = 1 – ,

где d_i - разности рангов; n - число пар рангов.

Для определения тесноты связи между тремя и более признаками применяется ранговый коэффициент согласия - коэффициент конкордации, который вычисляется по формуле:

w = ,

где m - количество факторов;

n - число наблюдений;

S - сумма квадратов отклонений рангов.

Величина коэффициента конкордации более 0,5 показывает, что между исследуемыми величинами имеется тесная зависимость.

Если при определении тесноты связи с помощью приведенных ранговых коэффициентов имеются связные ранги, т.е. если двум или более показателям присвоен один и тот же ранг, то расчеты проводятся по формулам:

коэффициент Спирмена: ρ_x/y = 1 – ;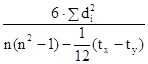

коэффициент конкордации: w = ,

где T = (t³ – t), а t - количество связных рангов по отдельным показателям.

При исследовании социальных явлений и процессов большое значение имеет изучение качественных показателей и признаков, не имеющих количественной оценки:

a	b	a + b
c	d	c + d
a + c	b + d	a + b + c + d

Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака (например, хороший, плохой).

Коэффициенты вычисляются по формулам:

A =  - ассоциации;

K =  - контингенции.

Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если A ³ 0,5, или K ³ 0,3.

Если каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициента взаимной сопряженности Пирсона. Этот коэффициент вычисляется по формуле:

C = ,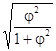

где j² - показатель взаимной сопряженности.

Расчет коэффициента взаимной сопряженности проводится по следующей схеме:

Группа признака A	Группа признака В			Итого
	B1	B2	B3
A1	f1	f2	f3	n1
A2	f4	f5	f6	n2
A3	f7	f8	f9	n3
	m1	m2	m3

Расчет j² проводится так:

по первой строке 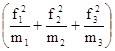 : n₁ = L₁;

по второй строке 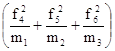 : n₂ = L₂;

по третьей строке 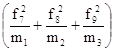 : n₃ = L₃;

Следовательно, j² = L₁ + L₂ + L₃ – 1.

Интерпретация непараметрических коэффициентов связи в некоторых случаях, особенно когда они имеют отрицательное значение, затруднительна. Их абсолютные значения могут изменяться в пределах от 0 до 1. Чем ближе абсолютные значения к единице, тем теснее связь между исследуемыми признаками.

Корреляция и регрессия. Традиционные методы корреляционно-регрессионного анализа позволяют не только оценить тесноту связи, но и выразить эту связь аналитически. Применению корреляционно-регрессионного анализа должен предшествовать качественный, теоретический анализ исследуемого социально-экономического явления или процесса.

Связь между двумя факторами аналитически выражается уравнениями:

прямой = a₀ + a₁x;

гиперболы = a₀ + ;

параболы = a₀ + a₁x + a₂x² (или другой ее степени);

степенной функции .

Параметр a₀ показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов. Параметр a₁ - коэффициент регрессии показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу. На основе этого параметра вычисляются коэффициенты эластичности, которые показывают изменение результативного признака в процентах в зависимости от изменения факторного признака на 1%:

Э = a₁∙.

Для определения параметров уравнений используется метод наименьших квадратов, на основании которого строится соответствующая система уравнений.

Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции:

r = ,

а при криволинейной зависимости с помощью корреляционного отношения:

h = .

Расчет коэффициентов регрессии несколько осложняется, если ряды по исследуемым факторам сгруппированы, а связь криволинейная.

Если зависимость между двумя факторами выражается уравнением гиперболы

= a₀ + ,

то система уравнений для определения параметров a₀ и a₁ такова:

na₀ + a₁∑ = ∑y;

a₀∑ + a₁∑ = ∑y.

Для определения параметров уравнения регрессии, выраженного степенной функцией , приводят функцию к линейному виду: lg= lga₀ + a₁lgx, отсюда система уравнений для определения параметров запишется:

n∙lga₀ + a₁∑lgx = ∑lgy;

lga₀∑lgx + a₁∑(lgx)² = ∑lgy∙lgx.

Зависимость между тремя и более факторами называется множественной или многофакторной корреляционной зависимостью. Линейная связь между тремя факторами выражается уравнением:

 = a₀ + a₁x + a₂z,

а система нормальных уравнений для определения неизвестных параметров a₀, a₁, a₂ будет следующей:

na₀ + a₁∑x + a₂∑z = ∑y;

a₀∑x + a₁∑x² + a₂∑zx = ∑yx;

a₀∑z + a₁∑xz + a₂∑z² = ∑yz.

Теснота связи между тремя факторами измеряется с помощью множественного (совокупного) коэффициента корреляции:

R = ,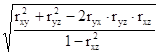

где r_ij - парные коэффициенты корреляции между соответствующими факторами.

Для более углубленного анализа вычисляются частные коэффициенты корреляции.

Дисперсионный анализ связи. При небольшом числе наблюдений исследовать влияние одного или нескольких факторных признаков на результативный можно, используя методы дисперсионного анализа. Дисперсионный анализ проводится расчетом дисперсий: общей, межгрупповой и внутригрупповой. Общую дисперсию называют дисперсией комплекса, межгрупповую - факторной, внутригрупповую - остаточной.

Дисперсионный анализ заключается в сравнении факторной и остаточной дисперсий. Если различие между ними значимо, то факторный признак, т.е. признак, положенный в основание группировки, оказывает существенное влияние на результативный. При исследовании воздействия на результативный признак только одного факторного, т.е. однофакторного комплекса дисперсии вычисляются:

дисперсия комплекса ;

факторная дисперсия ;

остаточная дисперсия ,

где n – 1, r – 1, n – r - соответствующие числа степеней свободы;

r - число уровней (групп).

На основании дисперсий проводится расчет критерия Фишера F_p. Если расчетное значение больше табличного, т.е. F_p > F_a, то существенность влияния факторного признака подтверждается.

Тема 10. Выборочное наблюдение

Главными вопросами теории выборочного наблюдения, требующими практического закрепления на основе решения задач и выполнения упражнений, являются:

- определение предела случайной ошибки репрезентативности для различных типов выборочных характеристик с учетом особенностей отбора;

- определение объема выборки, обеспечивающего необходимую репрезентативность выборочной характеристики, с учетом особенностей отбора.

Ошибка репрезентативности, или разность между выборочной и генеральной характеристикой (средней, долей), возникающая в силу несплошного наблюдения, в основе которого лежит случайный отбор, рассчитывается как предел наивероятной ошибки. В качестве уровня гарантийной вероятности обычно берется 0,954 или 0,997. Тогда предел ошибки определяется величиной удвоенной или утроенной средней ошибки выборки: D = 2m при P = 0,954; D = 3m при P = 0,997, или в общем виде D = tm (t - коэффициент, связанный с вероятностью, гарантирующей результат).

Величина средней ошибки выборки различна для отдельных разновидностей случайного отбора. При наиболее простой системе - собственно-случайном повторном отборе - средняя ошибка определяется следующими формулами:

индивидуальный отбор:

m =  = ,

где σ² - общая дисперсия признака;

n - число отобранных единиц наблюдения;

групповой (гнездовой, серийный) отбор:

m =  = ,

где δ² - межгрупповая дисперсия;

r - число отобранных групп (гнезд, серий) единиц наблюдения.

При практических расчетах ошибок репрезентативности необходимо учитывать следующее:

1. Вместо генеральной дисперсии используется соответствующая выборочная дисперсия. Так, вместо общей дисперсии доли в генеральной совокупности берется общая дисперсия частости:

 = w(1 – w) вместо  = pq.

2. В случае бесповторного способа отбора (а также механического) следует иметь в виду поправки (K) к ошибке повторной выборки на бесповторность отбора:

K =  < 1 или K = < 1.

Очевидно, что пользоваться этой поправкой целесообразно лишь тогда, когда относительный объем выборки составляет заметную часть генеральной совокупности (не менее 10%, тогда K £ 0,95).

3. При районированном отборе из типических групп единиц генеральной совокупности используется средняя из частных (групповых) дисперсий. Так, при индивидуальном отборе, пропорциональном размерам типических групп, имеем:

D = 2m = =  при P = 0,954,

где  - частная дисперсия i-й группы;

n_i - объем выборки в i-й группе.

Определение ошибок выборочных характеристик позволяет установить наивероятные границы нахождения соответствующих генеральных показателей:

для средней: ,

где  - генеральная средняя;

 - выборочная средняя;

 - ошибка выборочной средней;

для доли: p = w ± Dw,

где p - генеральная доля;

w - выборочная доля (частость);

Dw - ошибка выборочной доли.

Пример. С вероятностью 0,954 нужно определить границы среднего веса пачки чая для всей партии, поступившей в торговую сеть, если контрольная выборочная проверка дала следующие результаты (первые две графы табл. 10.1).

Таблица 10.1

Результаты взвешивания чая

Вес, г (x)	Количество пачек (m)	Расчетные графы
		x¢	m¢	x¢m¢	(x¢)2m¢
48 - 49	20	-1	2	-2	2
49 - 50	50	0	5	0	0
50 - 51	20	+1	2	2	2
51 - 52	10	+2	1	2	4
Итого:	100	–	10	2	8

1. Средний вес пачки чая по выборке:

 = ´ K + x₀ =  ´ 1 + 49,5 = 49,7 г.

2. Выборочная дисперсия веса пачки чая:

σ² = 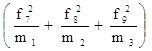= = 0,76.

3. Средняя ошибка выборочной средней:

=  =  = 0,087 г.

4. Предел для ошибки с вероятностью 0,954:

D = 2m = 0,174 г » 0,2 г.

5. Границы генеральной средней:

 = ± D = 49,7 ± 0,2 г.

Таким образом, с вероятностью 0,954 можно утверждать, что вес пачки чая в среднем для всей партии не более 49,9 г и не менее 49,5 г.

Определение объема выборки при заданной ее точности является проблемой, обратной рассмотренной нами - определению ошибки выборки при данном ее объеме. Формула объема выборки получается из соответствующей формулы предельной ошибки. Так, получаем для индивидуального бесповторного отбора:

n =;

группового бесповторного отбора:

r =.

При решении задач на определение необходимого объема выборки следует иметь в виду, что вместо генеральной дисперсии определенного вида берется ее оценка - примерное значение, полученное из того или иного источника. Рассмотрим следующий общий пример.

Пример. Нужно определить абсолютный и относительный объемы индивидуального отбора для исследования генеральной доли, чтобы ошибка частости с вероятностью 0,954 не превышала 0,02, если выборка производится из генеральной совокупности объема: а) 1000; б) 100000 единиц.

Используя формулу n =, в которой полагаем t = 2 (гарантийная вероятность равна 0,954), а pq = 0,25, имеем:

а) n =  = 714, или 71,4%;

б) n =  = 2439, или 2,44%.

Тема 11. Законы распределения

Конечной целью обработки информации методами математической статистика, если речь идет о больших выборках, является получение закона распределения исследуемой случайной величины. Это связано с тем, что закон распределения является фактически, тем аппаратом, который позволяет определить вероятность появления (или, наоборот, непоявления) случайной величины в тот или иной период времени или вероятность того, что случайная величина попадет в тот или иной интервал ее возможных значении. Этот этап статистической обработки является одним из наиболее важных, так как ошибка при выборе того или иного закона распределения приводит к ошибкам при дальнейшем решении практических задач.

Если проанализировать все этапы статистической обработки, то можно сделать вывод, что влекущими за собой наиболее существенные ошибки, а, следовательно, наиболее ответственными, являются этапы, на которых решаются следующие задачи:

1. Возможно ли объединение нескольких малых или средних выборок в одну.

2. Отбрасывать или учитывать резко отличающиеся результаты.

3. Справедливо ли сделанное предположение о законе распределения случайной величины.

Рассмотрим эти этапы более подробно.

1. Так как для установления закона распределения необходимы большие выборки, то на практике часто встает вопрос об объединении нескольких выборок, каждая из которых мала для решения поставленной задачи и получения одной общей выборки, удовлетворяющей предъявленным к ней требованиям. Поэтому, что вообще свойственно для статистической обработки, любое из неправильных решений (как положительное, так и отрицательное) по поводу объединения выборок приводит к нежелательным результатам, или к невозможности установить закон распределения, если выборки не объединяются, или к неправильному выводу о характере закона распределения.

Для решения этой задачи используют критерии, с помощью которых с разной формулировкой фактически дается ответ на один и тот же вопрос: принадлежат или не принадлежат исследуемые выборки одной генеральной совокупности, то есть автоматически решается задача о возможности или невозможности их объединения. Как правило, все эти критерии основаны на сравнении выборочных характеристик (выборочных дисперсий или средних величин) между собой или с соответствующими генеральными характеристиками. В большинстве случаев использование этих критериев предполагает нормальный или логарифмически-нормальный закон распределения для каждой выборки. При других же законах распределения эти критерии некорректны и их использование может привести к ошибочным результатам.

Наиболее используемыми являются следующие критерии:

а) критерии, основанные на сравнении дисперсий: критерий , критерий Фишера (F = ), критерий Хартлея (F_max = ), критерий Кочрена (G_max = ), критерий Бартлета (χ²);

б) критерии, основанные на сравнениях средних величин: критерий Стьюдента (t), критерий Z и другие.

Для всех критериев в качестве нулевой гипотезы (H₀) выдвигается предположение о принадлежности выборки генеральной совокупности или об однородности выборок между собой.

2. При наличии выборки, удовлетворяющей требованиям относительно ее пригодности для установления закона распределения перед тем, как приступить к определению статистических характеристик, необходимо проверить, принадлежат ли к данной выборке ее члены, резко отличающиеся от большинства данных, если таковые имеются. Такая проверка строго обязательна, так как любое неверное решение в отношении резко отличающихся результатов приводит к искажению вида кривой закона распределения и к последующим ошибкам, о которых уже говорилось выше. Описанная проверка также осуществляется с помощью соответствующих критериев: критерия Груббса (для малых выборок), критерия Ирвина и некоторых других. В качестве нулевой гипотезы во всех случаях принимается предположение о том, что резко выделяющиеся результаты принадлежат данной выборке.

3. Заключительной и самой трудоемкой проверкой является проверка гипотез о виде функции распределения или, что то же, о соответствии предполагаемого закона теоретического распределения эмпирическому. Эта проверка осуществляется с помощью так называемых критериев согласия. Существуют критерии для проверки соответствия как предполагаемому нормальному или логарифмически-нормальному закону распределения, так и любому другому закону распределения.

Наиболее используемыми при практических расчетах являются следующие критерии:

а) критерий Пирсона (χ²); он справедлив при больших объемах выборок и для любых законов распределения;

б) критерий Колмогорова-Смирнова (Du); этот критерий используется для проверки гипотезы о соответствии эмпирического распределения любому теоретическому закону распределения с заранее известными параметрами, что накладывает ограничения на его использование. В то же время Du является более мощным, чем критерий χ²;

в) критерий Крамера-Мизеса (w²); данный критерий используется для объемов выборок 50 £ n £ 200 и является более мощным, чем χ², однако, при его применении требуется больший объем вычислений. Поэтому при n > 200 этот критерий целесообразно использовать только в тех случаях, когда проверки гипотезы по другим критериям не приводят к безусловным результатам;

г) критерий Шапиро-Уилкса (W); он предназначен для проверки гипотезы о нормальном или логарифмически нормальном законе распределения при ограниченном объеме выборки (n £ 50) и является более мощным, чем другие критерии.

Укрупненно порядок проведения статистической обработки информации можно представить следующим образом: после решения вопроса об объеме выборки и принадлежности к ней резко отличающихся результатов, строится гистограмма, рассчитываются статистические характеристики исследуемой случайной величины, и устанавливается закон ее распределения.

При решении технических и экономических задач существует достаточно широкий круг законов распределения, которым подчиняются те или иные процессы. К ним относятся законы Вейбулла, Релея, экспоненциальный, гамма-распределения, однако, самыми распространенными являются нормальный (Гаусса) и логарифмически-нормальный законы распределения. Получив математическое выражение закона распределения, то есть соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, можно утверждать, что с вероятностной точки зрения, случайная величина описана полностью.