Навигация
Методы решения транспортной задачи
3. Методы решения транспортной задачи.
Транспортная задача может быть решена симплекс методом. Однако специфическая форма системы ограничений позволяет упростить симплекс метод.
МЕТОД СЕВЕРО-ЗАПАДНОГО УГЛА. Заполнение клеток происходит последовательно по следующему алгоритму: сначала вывозится груз из пункта А1 и завозится в пункт В1, и этой перевозке х11 присваивается максимально возможное значение. Если заявка пункта В1 выполнена, а в пункте А1 еще остается груз, то он вывозится в пункт В2 и т.д. Если в пункте А1 недостаточно было груза для В1, то недостающий груз берется из А2 и т.д.
После того как спрос потребителя А1 удовлетворен, он выпадает из рассмотрения и т.д.
| В1 | В2 | В3 | В4 | Запасы | |
| А1 | 15 5 | 5 7 | 6 | 8 | 20 |
| А2 | 6 | 25 7 | 8 | 5 | 25 |
| А3 | 5 | 5 4 | 25 6 | 7 | 30 |
| А4 | 6 | 5 | 10 7 | 5 4 | 15 |
| А5 | 5 | 6 | 6 | 10 6 | 10 |
| Заявки | 15 | 35 | 35 | 15 | 100 |
Стоимость перевозки: W=5*15+5*7+25*7+5*4+25*6+10*7+5*4+10*6=605
Существенным недостатком метода северо-западного угла является то, что он построен без учета стоимости перевозок.
МЕТОД МИНИМАЛЬНОГО ЭЛЕМЕНТА. Заполнение клеток транспортной таблицы начинается с той клетки, в которой значение минимально. В нее записывается максимально возможное значение перевозки хij, которое может быть равно либо запасу аi, либо заявке вj. Если заявка вj выполнена полностью, то j-й столбец больше не рассматривается. Если не вывезенный груз еще остался, то он вывозится в пункт с наименьшим тарифом.
| В1 | В2 | В3 | В4 | Запасы | |
| А1 | 15 5 | 7 | 5 6 | 8 | 20 |
| А2 | 6 | 7 | 25 8 | 5 | 25 |
| А3 | 5 | 30 4 | 6 | 7 | 30 |
| А4 | 6 | 5 | 7 | 15 4 | 15 |
| А5 | 5 | 5 6 | 5 6 | 6 | 10 |
| Заявки | 15 | 35 | 35 | 15 | 100 |
Стоимость перевозки: W = 30*4+5*6+15*4+15*5+5*6+25*8+5*6 = 545.
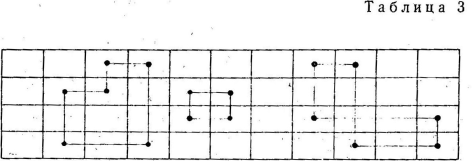
РАСПЕРЕДЕЛЕННЫЙ МЕТОД УЛУЧШЕНИЯ ПЛАНА ПЕРЕВОЗОК. Для улучшения плана используют цикл транспортной таблицы. Цикл – это несколько клеток, соединенных замкнутой ломанной с прямыми углами.
Изобразим два цикла: А1В1, А1В2, А2В2, А2В1; А1В3,А1В4, А2В4, А2В6, А1В5, А4В5, А4В3.
| поставщики | потребители | В1 | В2 | В3 | В4 | В5 | B6 | Мощность поставщиков |
| A1 | С11 | С12 | С13 | С14 | С15 | С16 | a1 | |
| A2 | С21 | С22 | С23 | С24 | С25 | С26 | a2 | |
| A3 | С31 | С32 | С33 | С34 | С35 | С36 | a3 | |
| А4 | С41 | С42 | С43 | С44 | С45 | С46 | а4 | |
| A5 | С51 | С52 | С53 | С54 | С55 | С56 | a5 | |
| Спрос потребителей | b1 | b2 | в3 | b4 | в5 | b6 |
| |
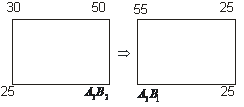
Каждый цикл имеет четное число вершин и ребер, то есть в таблице в каждой строке или столбце может находтся только четное число клеток, содержащих вершины. Поэтому в клетках-вершинах можно менять значения петевозки так, что в сумма по строкам и столбцам не изменяется. Вершины цикла, в которых увеличиваем перевозки «+», а в которых уменьшаем перевозки «-». Величину изменения обозначим ∆, ее будем перемещать по циклу. Максимальное значение ∆, на которое можно уменьшить перевозку, определяется условием неотрицательности перевозок.
Цена цикла q – это изменение стоимости перевозок при перемещении ∆ по циклу, которая равна разности между суммой стоимостей перевозок, соответствующих «+»-ым вершинам и суммой стоимостей «-» -ых вершин.
Q1= (с11+с22)-(с12+с21)
Q2 = (с13+с24+с16+с45)-(с14+с26+с15+с43)
При переносе по циклу к единиц груза, стоимость цикла и стоимость плана перевозок измениться на к единиц. Для улучшения плана перевозок нужно найти «-» цикл и переместить по нему максимально возможное количество груза, до тех пор пока таких циклов не останется. Количество груза, которое можно переместить определяется минимальным значением перевозок в «-» вершинах цикла.
Похожие работы
... продукции второго вида. В этом случае предприятие получит прибыль денежных единиц. 2. Решить транспортную задачу распределительным методом, оценивая свободные клетки по методу потенциалов. 60 50 85 75 65 8 10 6 5 65 80 4 30 3 50 5 9 35 11 25 4 4 8 10 90 5 5 5 3 85 6 Проверим необходимое ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... , является линейной функцией переменных : (2.4) Требуется в области допустимых решений системы уравнений (2.1) и (2.1.1) найти решение, минимизирующее линейную функцию (2.4). Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без ...
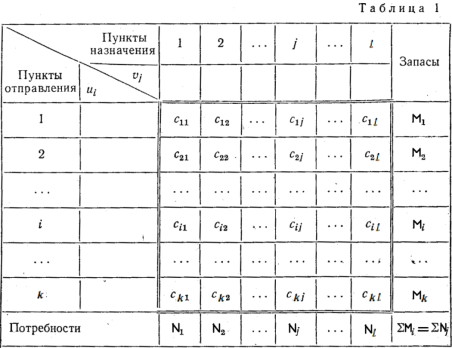
... метод потенциалов. Однако на распределительном методе основаны некоторые другие способы решения задач, что и вызывает необходимость его изучения. [5] 9. Метод потенциалов Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид. Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая ...





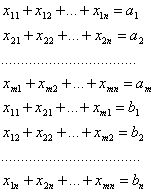



0 комментариев