Навигация
Аппроксимация переходного процесса по каналу внешнего возмущения
6.1.3. Аппроксимация переходного процесса по каналу внешнего возмущения.
Также по аналогии проводим аппроксимацию переходного процесса по каналу внешнего возмущения. Значение функции нормированной кривой заносятся в программу Linreg, после чего производится расчет передаточной функции объекта по каналу внешнего возмущения. Значения функций заносим в таблицу 6.1.3. График нормированной кривой по каналу внешнего возмущения на рисунке 6.1.3.
Таблица 6.1.3.
| Время с. | Значен. функц. | Время с. | Значен. функц. | Время с. | Значен. функц. | Время с. | Значен. функц. |
| 0 | 0,001 | 10 | 0,3131 | 20 | 0,6762 | 30 | 0,9162 |
| 1 | 0,0095 | 11 | 0,3486 | 21 | 0,7067 | 31 | 0,9314 |
| 2 | 0,019 | 12 | 0,3867 | 22 | 0,7371 | 32 | 0,9467 |
| 3 | 0,04 | 13 | 0,4267 | 23 | 0,7676 | 33 | 0,9619 |
| 4 | 0,0743 | 14 | 0,4686 | 24 | 0,7905 | 34 | 0,9771 |
| 5 | 0,1162 | 15 | 0,5105 | 25 | 0,8133 | 35 | 0,9867 |
| 6 | 0,1543 | 16 | 0,5467 | 26 | 0,8362 | 36 | 0,9924 |
| 7 | 0,1886 | 17 | 0,581 | 27 | 0,861 | 37 | 0,9962 |
| 8 | 0,2293 | 18 | 0,6114 | 28 | 0,88 | 38 | 0,9981 |
| 9 | 0,2712 | 19 | 0,6457 | 29 | 0,899 | 39 | 1,000 |
После проведения расчета передаточной функции получаем передаточную функцию следующего вида:
![]()
Коэффициент передачи в данном случае будет равен:
Кпер.= (12,7-3,95)/8,75=1
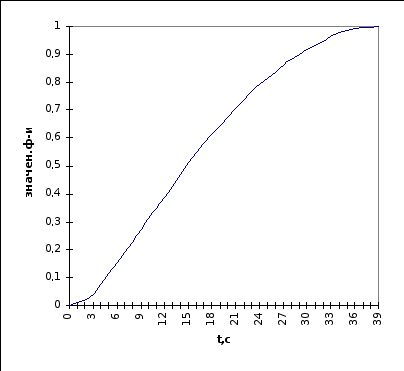
рис.6.1.3. График нормированной кривой по каналу внешнего возмущения
6.2. Проверка аппроксимации переходных процессов. 6.2.1. Проверка аппроксимации переходного процесса по основному каналу.
Проверку аппроксимации переходных процессов проводим с целью определения точности аппроксимации, путём получения переходного процесса "обратным путём". То есть - по полученным в разделе 6.1 передаточным функциям получаем кривую переходного процесса и сравниваем эту кривую с исходной. В идеальном случае - обе кривые должны совпасть.
Передаточная функция объекта по основному каналу равна:
![]()
Для определения переходного процесса воспользуемся программой Aproc - нахождение уравнения реакции системы на ступенчатое возмущение методом Карсона-Хевисайда. После ввода в программу коэффициентов передаточной функции, получим следующее математическое выражение
реакции системы на единичное ступенчатое воздействие y(t):
y(t) = 1 + 1.89 * Cos(4,15 - 0,07 * t) * exp(-0,11 * t).
Оформляем таблицу 6.2.1, в которой :
1 столбец - значения времени, с.
2 столбец - значения исходной кривой разгона, приведенной к безразмерной форме.
Хнорм. - значения точек нормированной кривой, приведенных в таблице 6.1.1
3 столбец - значения функции y(t)
4 столбец - абсолютная погрешность А, вычисленная по формуле:
А = Хнорм.(t) - y(t);
5 столбец - абсолютное значение разности квадратов Хнорм.(t) и y(t).
На рисунке 6.2.1 изображены исходная кривая переходного процесса и кривая, полученная преобразованием передаточной функции объекта (по данным столбцов 1 - 3 таблицы 6.2.1).
В 6 столбец записываем среднеквадратичное отклонение для двух функций, СКО = 0,007. Максимальная абсолютная погрешность составляет 2,4%.
Таблица 6.2.1.
| Время t,с | Хнормир.(t) | Y(t) | Абс.погрешн-ть А | Раз-ть квадратов Х2норм.-Y2(t) | СКО |
| 0 | 0.000 | 0.000 | 0.000 | 0.000 | 0.007 |
| 1 | 0.000 | 0.0078 | -0.0078 | 0.000 | |
| 2 | 0.0017 | 0.011 | 0.006 | 0.000 | |
| 3 | 0.0167 | 0.027 | 0.014 | 0.0005 | |
| 4 | 0.0467 | 0.059 | -0.0123 | 0.001 | |
| 5 | 0.0933 | 0.101 | -0.0077 | 0.002 | |
| 6 | 0.1433 | 0.165 | -0.0217 | 0.006 | |
| 7 | 0.2083 | 0.233 | -0.0247 | 0.01 | |
| 8 | 0.277 | 0.2988 | -0.0218 | 0.012 | |
| 9 | 0.346 | 0.3517 | -0.0057 | 0.004 | |
| 10 | 0.411 | 0.4039 | 0.01 | 0.005 | |
| 11 | 0.4713 | 0.4548 | 0.019 | 0.01 | |
| 12 | 0.5293 | 0.5038 | 0.02 | 0.02 | |
| 13 | 0.5763 | 0.574 | 0.002 | 0.003 | |
| 14 | 0.624 | 0.619 | 0.005 | 0.006 | |
| 15 | 0.6687 | 0.666 | 0.002 | 0.004 | |
| 16 | 0.709 | 0.7117 | -0.002 | 0.004 | |
| 17 | 0.7457 | 0.745 | 0.0007 | 0.001 | |
| 18 | 0.7787 | 0.7756 | 0.003 | 0.004 | |
| 19 | 0.808 | 0.8036 | 0.005 | 0.007 | |
| 20 | 0.8297 | 0.8289 | 0.0006 | 0.001 | |
| 21 | 0.8517 | 0.8519 | -0.0002 | 0.0001 | |
| 22 | 0.8723 | 0.8725 | -0.0002 | 0.0001 | |
| 23 | 0.889 | 0.887 | 0.002 | 0.003 | |
| 24 | 0.904 | 0.911 | -0.007 | 0.01 | |
| 25 | 0.9173 | 0.920 | -0.003 | 0.005 | |
| 26 | 0.931 | 0.934 | -0.003 | 0.005 | |
| 27 | 0.9393 | 0.935 | 0.004 | 0.008 | |
| 28 | 0.947 | 0.9463 | 0.001 | 0.001 | |
| 29 | 0.9533 | 0.9562 | -0.002 | 0.005 | |
| 30 | 0.9597 | 0.9648 | -0.005 | 0.01 | |
| 31 | 0.9653 | 0.9723 | -0.007 | 0.01 | |
| 32 | 0.9707 | 0.9787 | -0.008 | 0.01 | |
| 33 | 0.976 | 0.9841 | -0.008 | 0.01 | |
| 34 | 0.98 | 0.9887 | -0.008 | 0.01 | |
| 35 | 0.983 | 0.9926 | -0.009 | 0.008 | |
| 36 | 0.9847 | 0.9958 | -0.011 | 0.02 | |
| 37 | 0.9867 | 0.9985 | -0.012 | 0.01 | |
| 38 | 0.9883 | 1.0006 | -0.012 | 0.009 | |
| 39 | 0.992 | 1.0023 | -0.01 | 0.01 | |
| 40 | 0.994 | 1.0037 | -0.009 | 0.01 | |
| 41 | 0.996 | 1.0047 | -0.008 | 0.009 | |
| 42 | 0.9963 | 1.0054 | -0.009 | 0.01 | |
| 43 | 0.9967 | 1.006 | -0.009 | 0.01 | |
| 44 | 0.9977 | 1.0063 | -0.002 | 0.01 | |
| 45 | 1.000 | 1.0065 | -0.0065 | 0.01 | |
| Сумма | 0.3327 |
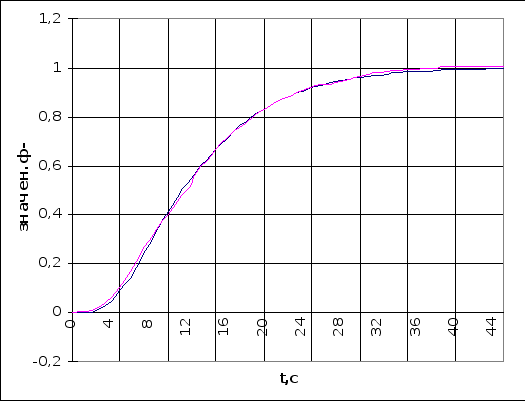
рис 6.2.1. Проверка аппроксимации переходного процесса по основному каналу.
6.2.2. Проверка аппроксимации кривой переходного процесса по внутреннему каналу.
Для получения математического выражения реакции внутреннего канала на единичное воздействие воспользуемся программой Aproc. Передаточная функция объекта по внутреннему каналу имеет вид:
![]()
Вводим в программу коэффициенты передаточной функции и после расчёта получаем следующее выражение реакции внутреннего канала на единичное ступенчатое воздействие:
y(t) = 1 + 1,57 * Cos(4,02 - 0,14 * t) * exp(-0,17 * t).
Далее, аналогично таблице 6.2.1 оформляем таблицу 6.2.2. Значения столбцов 1, 2 заполняем в соответствии с таблицей 6.1.2.
По значениям первых трёх столбцов строим исходную кривую переходного процесса, а так же кривую полученную путём перехода к оригиналу по Карсону-Хевисайду (рисунок 6.2.2).
Таблица 6.2.2.
| Время t,c | Хнор.(t) | Y(t) | Абс.погр. А | Разность Х2нор.(t)-Y2(t) | СКО |
| 0 | 0 | 0.000 | 0.000 | 0.000 | 0.02 |
| 1 | 0.0256 | 0.0206 | 0.005 | 0.0002 | |
| 2 | 0.0513 | 0.065 | -0.01 | 0.001 | |
| 3 | 0.0798 | 0.12 | -0.04 | 0.008 | |
| 4 | 0.1311 | 0.19 | -0.047 | 0.01 | |
| 5 | 0.2194 | 0.264 | -0.04 | 0.02 | |
| 6 | 0.3476 | 0.37 | -0.02 | 0.01 | |
| 7 | 0.4786 | 0.5086 | -0.03 | 0.02 | |
| 8 | 0.5983 | 0.63 | -0.03 | 0.03 | |
| 9 | 0.698 | 0.737 | -0.039 | 0.05 | |
| 10 | 0.8006 | 0.837 | -0.036 | 0.05 | |
| 11 | 0.8989 | 0.93 | -0.031 | 0.05 | |
| 12 | 0.9993 | 1.000 | -0.0007 | 0.001 | |
| 13 | 1 | 1.02 | 0.02 | 0.04 | |
| Сумма | 0.2902 |
Из таблицы видно, что среднеквадратичное отклонение исходной кривой от полученной из передаточной функции по Карсону-Хевисайду составляет 0,02 %, максимальная абсолютная погрешность - 4,7 %. Следовательно, можно считать что исходная кривая аппроксимирована с достаточной точностью.
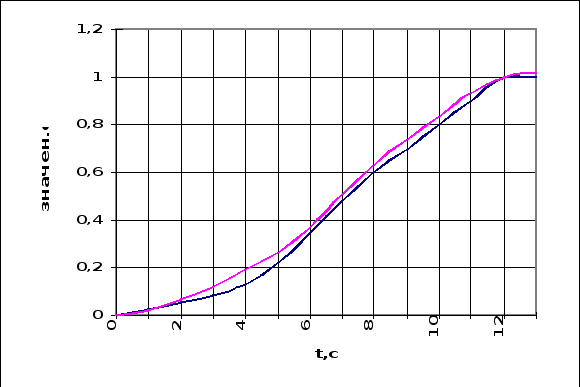
рис.6.2.2.Проверка аппроксимации переходного процесса по внутреннему каналу.
6.2.3. Проверка аппроксимации переходного процесса по каналу внешнего возмущения.
Проверку аппроксимации переходного процесса по каналу внешнего возмущения проводим в такой же последовательности, как и в разделах, описанных выше.
Передаточная функция объекта по каналу внешнего возмущения равна:
![]()
Для определения переходного процесса воспользуемся программой Apron - нахождение уравнения реакции системы на ступенчатое возмущение методом Карсона-Хевисайда. После ввода в программу коэффициентов передаточной функции, получим следующее математическое выражение реакции системы на единичное ступенчатое воздействие y2(t):
y(t) = 1 + 1,94 * Cos(4,17 - 0,06 * t) * exp(-0,09 * t).
Оформляем таблицу 6.2.3 (аналогично таблице 6.2.1). По значениям столбцов 1-3 строим графики исходной кривой разгона объекта по каналу
внешнего возмущения и кривую, полученную из передаточной функции по Карсону-Хевисайду.
Среднеквадратичное отклонение исходной кривой от полученной составляет 0,01 %, максимальная абсолютная погрешность - 2%. Следовательно, можно считать что исходная кривая аппроксимирована с достаточной точностью.
Таблица 6.2.3.
| Время t,c | Хнорм.(t) | Y(t) | Абс.погр. А | Разность Х2н.(t)-Y2(t) | СКО |
| 0 | 0.001 | 0.000 | 0.001 | 0.000 | 0.01 |
| 1 | 0.0095 | 0.0055 | 0.004 | 0.000 | |
| 2 | 0.019 | 0.0205 | -0.0015 | 0.000 | |
| 3 | 0.04 | 0.0434 | -0.003 | 0.000 | |
| 4 | 0.0743 | 0.0726 | 0.0017 | 0.000 | |
| 5 | 0.1162 | 0.1066 | 0.009 | 0.002 | |
| 6 | 0.1543 | 0.1444 | 0.0099 | 0.003 | |
| 7 | 0.1886 | 0.1849 | 0.004 | 0.001 | |
| 8 | 0.2293 | 0.2272 | 0.002 | 0.001 | |
| 9 | 0.2712 | 0.2705 | 0.0007 | 0.0004 | |
| 10 | 0.3131 | 0.3143 | -0.001 | 0.0007 | |
| 11 | 0.3486 | 0.3579 | -0.009 | 0.006 | |
| 12 | 0.3867 | 0.401 | -0.01 | 0.01 | |
| 13 | 0.4267 | 0.4432 | -0.01 | 0.01 | |
| 14 | 0.4686 | 0.4841 | -0.015 | 0.015 | |
| 15 | 0.5105 | 0.5237 | -0.01 | 0.014 | |
| 16 | 0.5467 | 0.5616 | -0.015 | 0.016 | |
| 17 | 0.581 | 0.5977 | -0.0167 | 0.02 | |
| 18 | 0.6114 | 0.632 | -0.02 | 0.025 | |
| 19 | 0.6457 | 0.6645 | -0.02 | 0.02 | |
| 20 | 0.6762 | 0.695 | -0.018 | 0.02 | |
| 21 | 0.7067 | 0.7236 | -0.017 | 0.02 | |
| 22 | 0.7371 | 0.7503 | -0.013 | 0.02 | |
| 23 | 0.7676 | 0.7752 | -0.007 | 0.01 | |
| 24 | 0.7905 | 0.7983 | -0.007 | 0.01 | |
| 25 | 0.8133 | 0.8196 | -0.006 | 0.01 | |
| 26 | 0.8362 | 0.8392 | -0.003 | 0.005 | |
| 27 | 0.861 | 0.8572 | 0.004 | 0.006 | |
| 28 | 0.88 | 0.8737 | 0.006 | 0.01 | |
| 29 | 0.899 | 0.888 | 0.01 | 0.01 | |
| 30 | 0.9162 | 0.9025 | 0.0137 | 0.02 | |
| 31 | 0.9314 | 0.924 | 0.007 | 0.01 | |
| 32 | 0.9467 | 0.934 | 0.01 | 0.02 | |
| 33 | 0.9619 | 0.948 | 0.0139 | 0.026 | |
| 34 | 0.9771 | 0.96 | 0.0171 | 0.03 | |
| 35 | 0.9867 | 0.978 | 0.009 | 0.02 | |
| 36 | 0.9924 | 0.989 | 0.003 | 0.006 | |
| 37 | 0.9962 | 0.9872 | 0.009 | 0.02 | |
| 38 | 0.9981 | 0.9929 | 0.005 | 0.01 | |
| 39 | 1.000 | 0.9989 | 0.001 | 0.002 | |
| Сумма | 0.4291 |
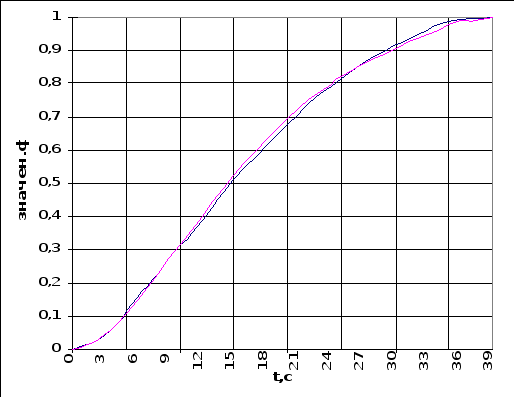
рис.6.2.3.Проверка аппроксимации переходного процесса по каналу внешнего возмущения.
6.3. Расчёт оптимальных настроек регулятора одноконтурной АСР.Для расчёта настроек регулятора одноконтурной АСР вводим в основную программу Linreg передаточную функцию объекта по основному каналу:
![]()
Расчёт проводим для ПИ-регулятора методом Ротача, получаем следующие настройки регулятора:
Кп = 3,15;
Ти = 12,6.
На рисунках 6.3.1 и 6.3.2 изображены кривые переходных процессов для одноконтурной АСР при полученных настройках регулятора при управляющем и возмущающем воздействии соответственно.
Величины максимального отклонения регулируемой величины составляют: 30 % - при управляющем воздействии, и 26 % - при возмущающем.
Настройки регулятора посчитаны для степени затухания 0,9. Уменьшение степени затухания приводит к увеличению величины перерегулированияв переходном процессе при управляющем воздействии.
Большие значения перерегулирования в переходных процессах обусловлены свойствами объекта регулирования.
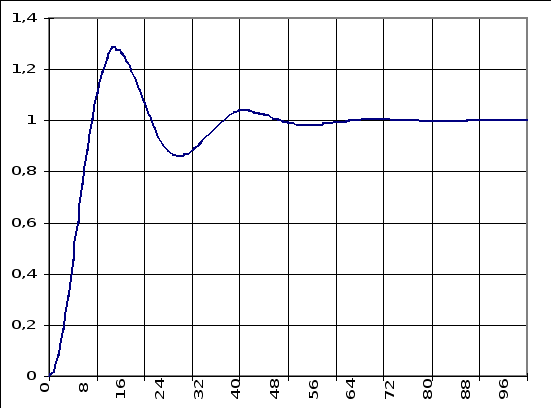
рис.6.3.1. Кривая переходного процесса для одноконтурной АСР при управляющем воздействии.
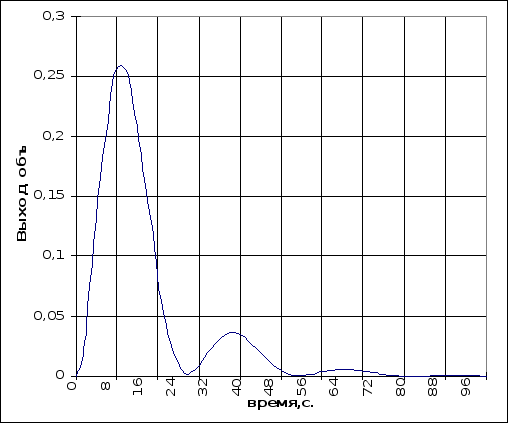
6.4. Расчет оптимальных настроек регуляторов каскадной АСР.
Для более оптимального ведения процесса нейтрализации, поддержания технологических параметров на заданном уровне (в данном дипломном проекте это величина рН сточных вод), предлагаю реализовать каскадно-комбинированную схему АСР с компенсацией по возмущению.
Каскадная система регулирования является схема, в которой вводится дополнительная стабилизация некоторой промежуточной величины дополнительным регулятором. Структурная схема имеет следующий вид:







![]()
![]() Xy Wp1 Wp2 Xp WO.K. X
Xy Wp1 Wp2 Xp WO.K. X
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() X1 WB.K.
X1 WB.K.
![]()
![]()
рис.6.4.1.Структурная схема каскадной АСР.
Регулятор Wp1 контролирует основную величину “Х” и при ее отклонении воздействует не на регулирующий орган, а на задатчик регулятора Wp2. Регулятор Wp2 в свою очередь поддерживает на заданном значении вспомогательную величину Х1.
Объект WB.K. с регулятором Wp2 образуют внутренний контур системы или стабилизирующий.
Объект WO.K. c регулятором Wp1 называют внешним контуром или корректирующим.
Расчет оптимальных настроек регуляторов для каскадной АСР будем проводить в следующей последовательности:
1.- Определяем настройки регулятора внутреннего контура.
2.- Определяем вид передаточной функции для эквивалентного объекта.
3.- По передаточной функции эквивалентного объекта определяем настройки регулятора для внешнего контура.
Настройки регулятора внутреннего контура определяем по передаточной функции внутреннего канала объекта:
![]()
Расчет проводим аналогично расчету одноконтурной АСР. Получаем следующие настройки регулятора:
КП=2,56;
ТИ=7,47.
Переходные процессы внутреннего контура с полученными настройками регулятора по управлению и возмущению изображены на рисунках 6.4.1 и 6.4.2.
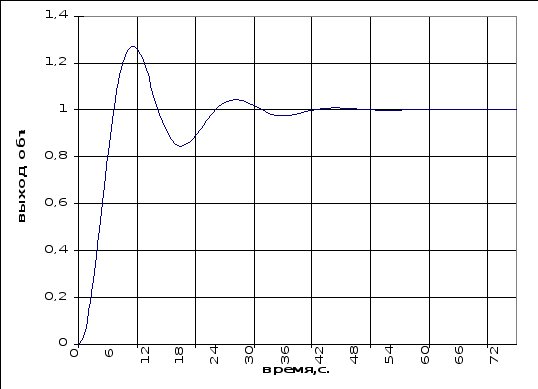
рис.6.4.2.График переходного процесса внутреннего контура по управляющему воздействию.
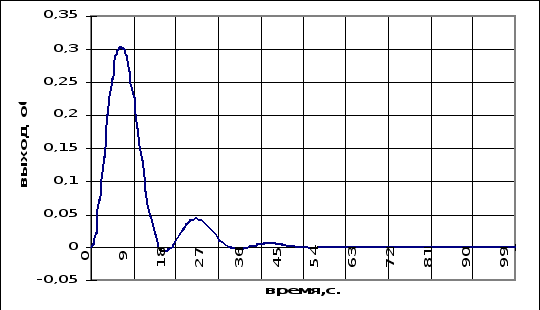
рис.6.4.3.График переходного процесса внутреннего контура при возмущающем воздействии.
Данные, которые были только что произведены понадобятся в дальнейшем для расчета эквивалентного объекта и пересчета настроек регулятора для каскадной АСР.
Итак рассчитываем передаточную функцию для эквивалентного объекта по следующей формуле:
Wэкв.(S)![]()
WР1(S) - передаточная функция стабилизирующего регулятора:
![]() )
)
![]()
WO.K(S) - передаточная функция основного канала.
WB.K.(S) - передаточная функция внутреннего канала.
Запишем следующую передаточную функцию эквивалентного объекта:
Wэкв.(S)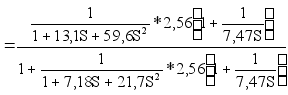
При дальнейших вычислениях получаем передаточную функцию эквивалентного объекта следующего вида:
Wэкв.(S)![]()
По полученной передаточной функции эквивалентного объекта находим настроечные параметры для корректирующего регулятора:
Кп = 0,49;
Ти = 1,46.
На рисунках 6.4.3 и 6.4.4 изображены графики переходных процессов по управлению и по возмущению для каскадной АСР.
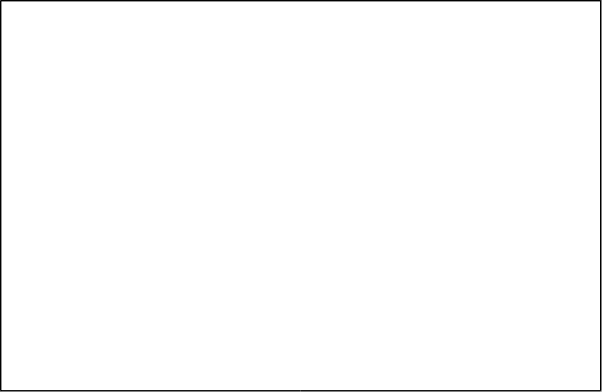
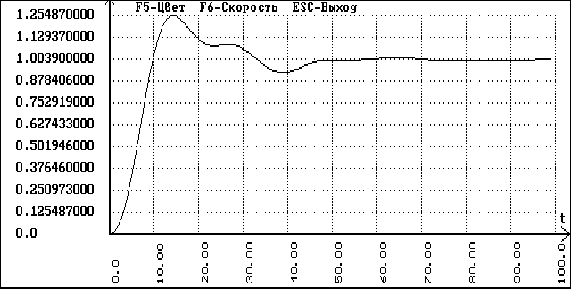
рис.6.4.3. График переходного процесса для каскадной АСР по управлению
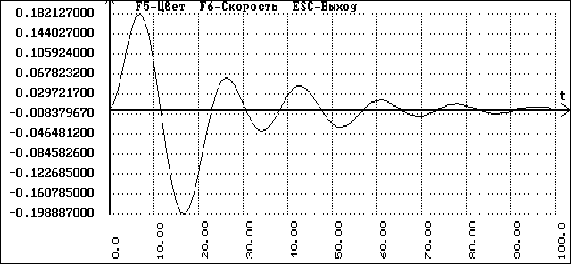
 рис.6.4.4.
График переходного
процесса для
каскадной АСР
по возмущению.
рис.6.4.4.
График переходного
процесса для
каскадной АСР
по возмущению.
6.5 Расчет настроек регулятора комбинированной АСР.
Введение добавочных контуров регулирования способствует повышению точности работы системы. Схема, предложенная на рисунке 6.5.1 называется комбинированной схемой регулирования с компенсацией по возмущению. Выход компенсирующего устройства подается на вход регулятора.


![]()
![]()
![]()
![]() WK
WK


![]() WВОЗ.
WВОЗ.




![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() X Wp1 Wp2 WO.K Y
X Wp1 Wp2 WO.K Y
![]()
![]()
![]()
WB.K.
![]()
![]()
рис.6.5.1. Структурная схема комбинированной АСР.
Добавочное звено WK, которое появилось в данной схеме, является фильтром, через который
проходит возмущающее воздействие, прежде чем войти в систему в виде управляющего воздействия “Х”.
Преимущество комбинированной системы заключается в том, что увеличение фильтрующей способности фильтра может быть достигнута не только изменением настроечных параметров регулятора, но также изменением настроек компенсирующего устройства.
Сначала необходимо найти передаточную функцию эквивалентного фильтра. Передаточную функцию рассчитываем по формуле:
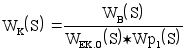
где
WB(S)- передаточная функция по каналу внешнего возмущения
WЭК.О(S)-передаточная функция эквивалентного объекта для каскадной АСР.
Wp1(S)-передаточная функция регулятора по основному каналу.
Подставляем в выражение значения передаточных функций и получаем следующее выражение:
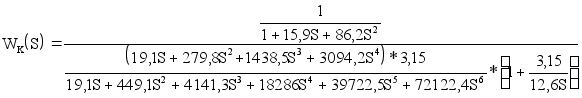
После расчета получаем передаточную функцию эквивалентного компенсатора следующего вида:
![]()
Затем проводим расчет настроечных параметров компенсатора. Расчет ведем для нулевой и критической частоты. Для этого полученную передаточную функцию заводим в программу “Linrеg”. Снимаем КЧХ и записываем значения Re и Im для частот =0 и критической частоты по основному каналу =0.21827. Получаем следующие значения:
| | Re | Im |
| 0 | 0 | 0 |
| 0.21827 | 0.101 | 0.00412 |
Коэффициенты компенсатора определяем геометрически на рисунке 6.5.2.

![]()
![]() Im
Im
![]()
![]()

![]()
![]()
![]()
 0.06
0.06
![]()
0.04
![]() 0.02
0.02
C D
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0
0
0.02 0.04 0.06 0.08 0.1 0.102 0.104 Re
рис.6.5.2.Графический метод определения настроечных параметров компенсатора.
Из графика видно, что:
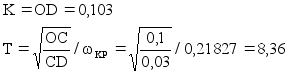
6.6 Моделирование переходных процессов
Для моделирования переходных процессов одноконтурных АСР по возмущению и по управлению, а также каскадной АСР по возмущению и по управлению и комбинированной системы с компенсатором и без него воспользуемся программой “SIAM”
Схема одноконтурной АСР по управляющему воздействию предоставлена на рисунке 6.6.1, где
1. W(S)- объект-передаточная функция основного канала;
2. К-коэффициент пропорциональности регулятора основного канала, 3.15
3. K/S-значение Кп/Ти = 3.15/12.6 = 0.25
На рисунке 6.6.2 изображен график отклика схемы на единичный скачок.

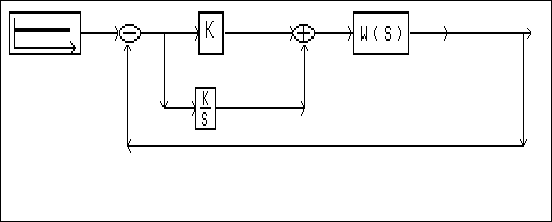
рис.6.6.1.Схема одноконтурной АСР основного канала по управлению
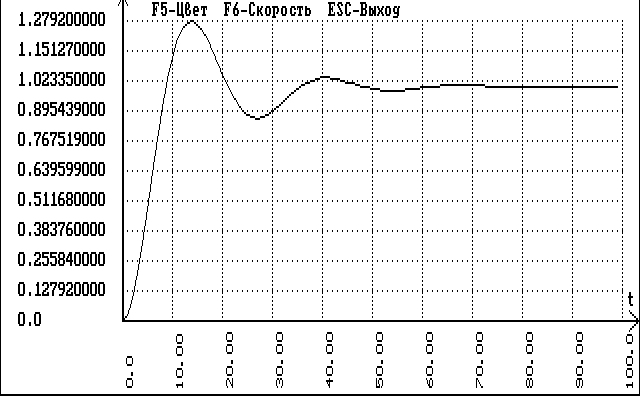
рис.6.6.2 График отклика одноконтурной АСР по основному каналу на управляющее воздействие.
Схема переходного процесса основного канала по возмущению предоставлена на рисунке 6.6.3. Настройки звеньев схемы такие же как и в предыдущей схеме.
График отклика схемы на возмущение изображен на рисунке 6.6.4.

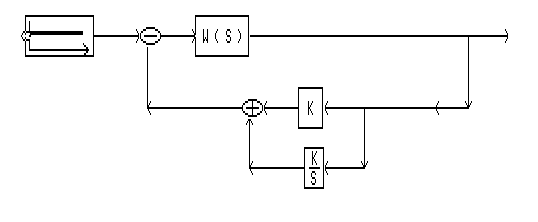
рис.6.6.3 Схема одноконтурной АСР основного канала по возмущению
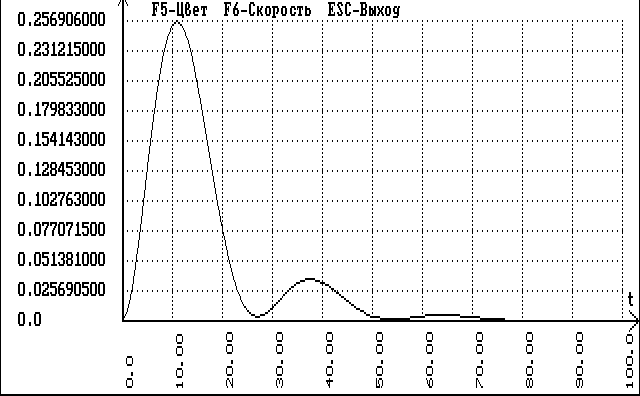
рис.6.6.4.График отклика одноконтурной АСР по основному каналу на возмущение
Модель каскадной АСР по управлению приведена на рисунке 6.6.5.

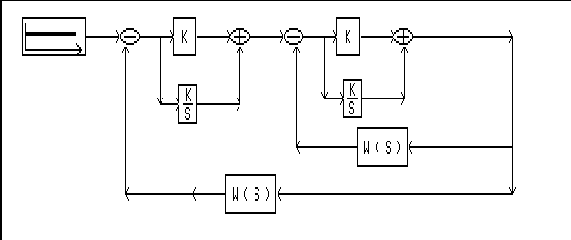
рис.6.6.5 Модель каскадной АСР по управлению
1.К-коэффициент пропорциональности регулятора эквивалентного объекта 0.49
2. K/S-значение Кп/Ти = 0.49/1.46 = 0.33
3. К-коэффициент пропорциональности регулятора внутреннего канала 2.56
4. K/S-значение Кп/Ти = 2.56/7.47 = 0.34
5.W(S)-передаточная функция внутреннего канала
6.W(S)-передаточная функция основного канала
График отклика модели на управляющее воздействие предоставлен на рисунке 6.6.6. График снимаем со звена 5.

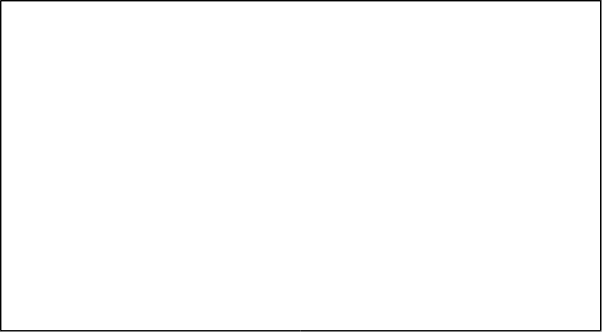
рис.6.6.6.График отклика модели каскадной АСР по управлению.
Модель каскадной АСР по возмущению предоставлена на рисунке 6.6.7., где:
1.W(S)-передаточная функция объекта по основному каналу
2.W(S)-передаточная функция объекта по внутреннему каналу
3.К-коэффициент пропорциональности регулятора эквивалентного объекта Кп=0.49
4.K/S-значение Кп/Ти = 0.49/1.46 = 0.33
5.К-коэффициент пропорциональности регулятора внутреннего канала Кп=2.56
6.K/S-значение Кп/Ти = 2.56/7.47 =0.34
7.К-блок усиления входного сигнала К=-1
График отклика модели на возмущение изображен на рисунке 6.6.8.
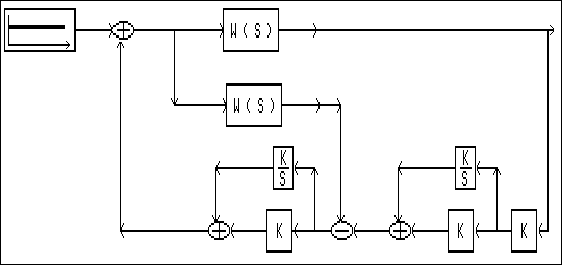
рис.6.6.7 Модель каскадной АСР по возмущению

рис.6.6.8.График отклика модели каскадной АСР по возмущению
Модель комбинированной АСР без компенсатора изображена на рисунке 6.6.9., где:
1.W(S)-передаточная функция объекта по возмущению;
2.К-коэффициент пропорциональности регулятора эквивалентного объекта Кп=0.49
3.K/S-интегрирующее звено, значение Кп/Ти =0.49/1.46=0.33;
4.К-коэффициент пропорциональности регулятора внутреннего контура объекта Кп=2.56;
5.K/S-интегрирующее звено, значение Кп/Ти=2.56/7.47=0.34;
6.W(S)-передаточная функция объекта по внутреннему каналу;
7.W(S)-передаточная функция объекта по основному каналу;
8.К-коэффициент усиления входного сигнала К=-1;
9.К-коэффициент усиления входного сигнала К=-1.
График отклика модели на возмущение изображен на рисунке 6.6.10.

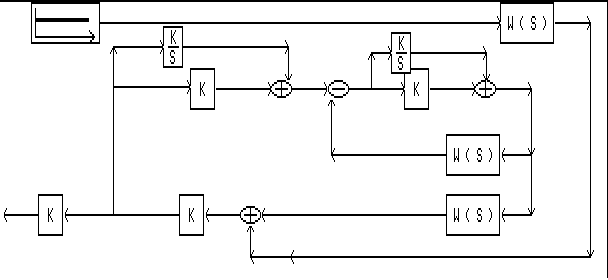
рис.6.6.9.Модель комбинированной АСР без коипенсатора.

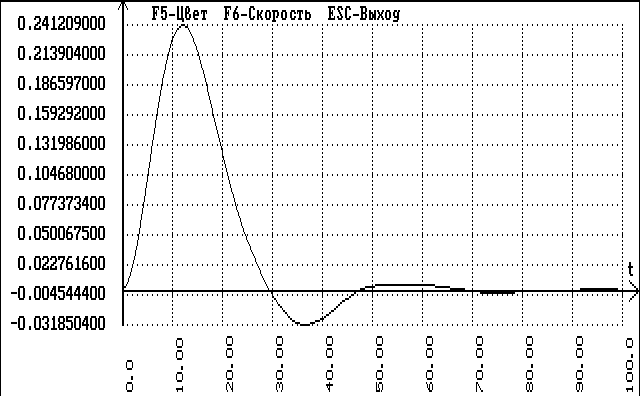
рис.6.6.10.График отклика комбинированной АСР без компенсатора на возмущение
Модель комбинированной АСР с компенсатором изображена на рисунке 6.6.11., где:
1.W(S)-передаточная функция объекта по каналу внешнего возмущения
2.К-коэффициент усиления входного сигнала К=0.103
3.K/TS+1-передаточная функция компенсатора, в функцию заносятся коэффициенты К=0.103 и Т=8.36
4.К-коэффициент пропорциональности регулятора эквивалентного объекта Кп=0.49
5.K/S-интегрирующее звено, значение Кп/Ти = 0.49/1.46 = 0.33
6.К-коэффициент пропорциональности регулятора внутреннего контура объекта Кп=2.56
7.K/S-интегрирующее звено, значение Кп/Ти = 2.56/7.47 = 0.34
8.W(S)-передаточная функция объекта по внутреннему каналу
9.W(S)-передаточная функция объекта по основному каналу
10.К-коэффициент усиления входного сигнала К=-1
11.К-коэффициент усиления входного сигнала К=-1
График отклика модели на возмущающее воздействие изображен на рисунке 6.6.12.
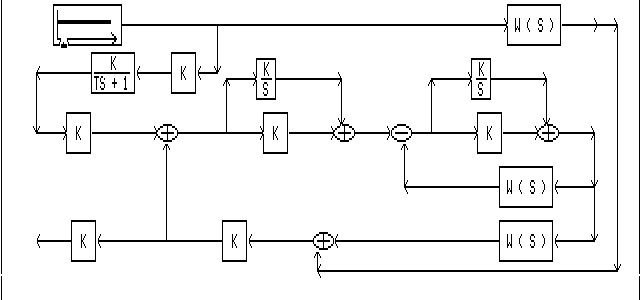
рис.6.6.11.Модель комбинированной АСР с компенсатором
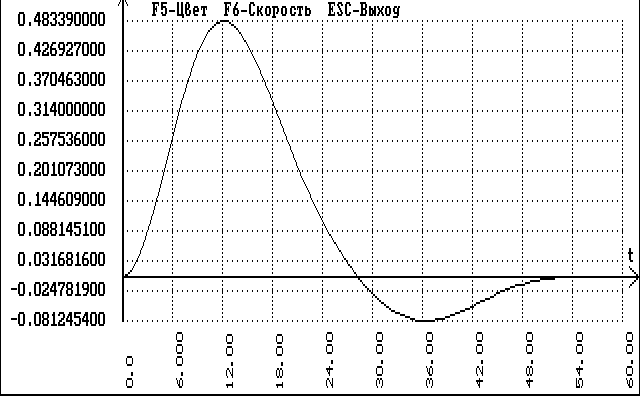
рис.6.6.12.График отклика модели комбинированной АСР с компенсатором на возмущение.
Похожие работы
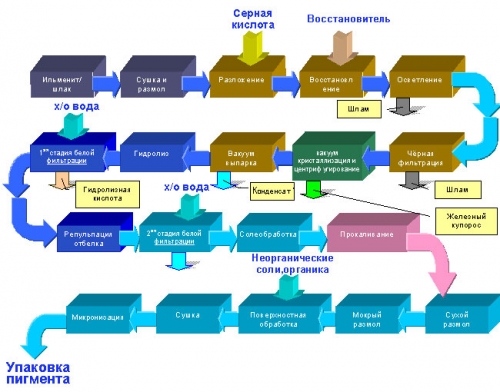
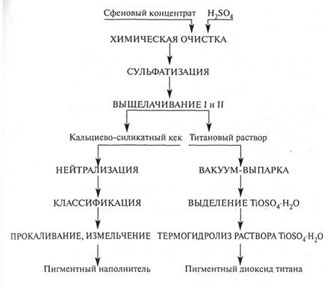
... раствор после выделения соли полностью возвращается на сульфатизацию, вследствие чего существенно снижается расход серной кислоты (до 3,5—4,5 т на 1 т диоксида титана). Принципиальная схема переработки сфенового концентрата Глава 2. ИЗВЛЕЧЕНИЕ СЕРНОЙ КИСЛОТЫ ИЗ ОТХОДОВ ПРОЦЕССА ПРОИЗВОДСТВА ДИОКСИДА ТИТАНА Процесс, разработанный К. X. Дёрром предназначен для выделения серной кислоты из ...
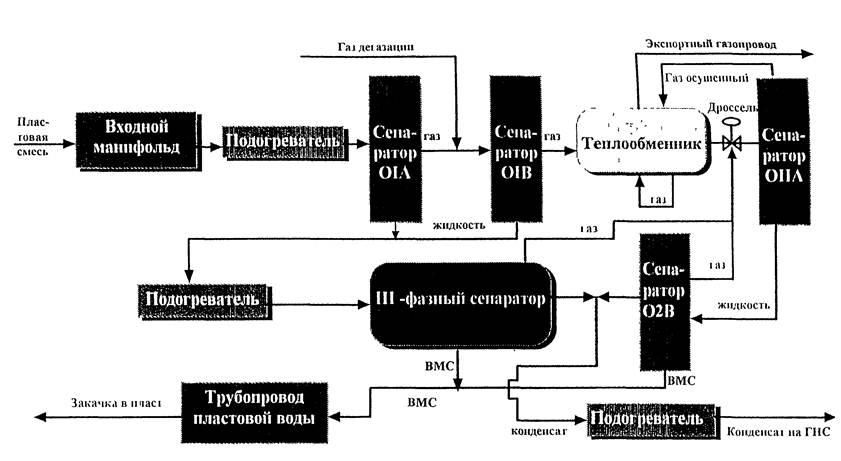
... от кислых газов (м3/с) Концентрированные кислые газы, полученные при регенерации метанола, общим потоком подаются на установку переработки кислых газов с получением товарной серы. Из практики известно, что в промышленных условиях при очистке природного газа от кислых газов метанолом с последующим выделением кислых газов при регенерации, получают концентрированный кислый газ, содержащий 58% Н2S ...
... состоянии – создают серьезные трудности аппаратурного и технологического характера при разработке и практической реализации теплообменных и массообменных процессов и аппаратов. И хотя создание и развитие хлорной металлургии титана и редких металлов явилось причиной появления большого числа работ по химии парообразного состояния – совершенно нового направления в химии – проблема как в научном, так ...
... расчет величины затрат необходимых для внедрения этого проекта в производство. Оценить изменение себестоимости продукции получаемой в цехе первичной переработки нефти и получения битума. В цехе установлено две печи: для нагрева нефти П-1 и для подогрева мазута и пара П-3, после реконструкции должна быть установлена печь, которая полностью заменит обе печи П-1 и П-3. Производительность печи по ...

0 комментариев